什么是树?
树(Tree)是n(n≧0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:有且仅有一个特定的称为根的结点。当n>1时,
其余结点可分为m(m>0)个互不相交的有限集T1、T2、T3……、Tm,其中每个集合本身又是一棵树,并且称为根的子树。
树中有一个称为“根(Root)”的特殊结点,用r表示
除了根结点外,每个结点有且仅有一个父结点
一棵N个结点的树有N-1条边
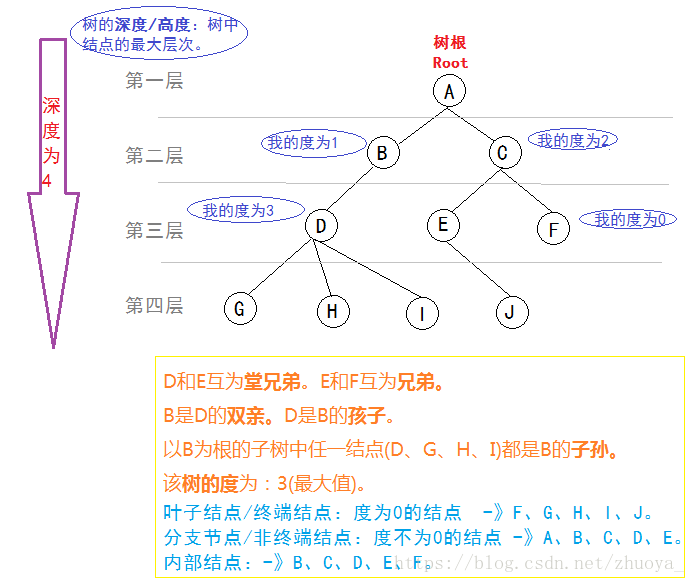
树的基本术语
结点的度(Degree):结点的子树个数
树的度:树的所有结点中最大的度数
叶节点(Leaf):度为0的结点
父结点(Parent):有子树的结点是其子树的根结点的父结点
子结点(Child):若 A 结点是 B 结点的父结点,则称 B 结点是 A 结点的子结点,也称孩子结点
兄弟结点(Sibling):具有同一父结点的各个结点彼此是兄弟结点
路径和路径长度:从结点n1到nk的路径为一个结点序列n1、n2...nk,路径所包含边的个数为路径长度
祖先结点(Ancestor):沿树根到某一结点路径上的所有结点都是这个结点的祖先结点
子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙
结点的层次(Level):规定根结点在 1 层,其他任一结点的层数是其父结点的层数加一
树的深度(Depth):树中所有结点中的最大层次是这棵树的深度
定义树的时候需要注意的两点:
n>0时,根的节点是唯一的,不可能存在多个根结点。
m>0时,子树的个数没有限制,子树一定是不相交的。
课后习题
【2010年真题】在一棵度为 4 的树 T 中,若有 20 个度为 4 的结点,10 个度为 3 的结点,1 个度为 2 的结点,10 个度为 1 的结点,则树 T 的叶结点个数是()。
A.41 B.82 C.113 D.122
参考答案:B
答案解析:考查树结点数的特性。
设树中度为 i(i=0,1,2,3,4)的结点数分别为 Ni,树中结点总数为 N,则树中各结点的度之和等于 N-1,即 N = 1+N1+2N2+3N3+4N4 = N0+ N1+N2+N3+N4,根据题设中的数据,即可得到 N0 = 82,即树 T 的叶结点的个数是 82。


 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1



登录后开始许愿
暂无评论,来抢沙发