二叉树的存储结构有两种，分别为顺序存储和链式存储。

二叉树的顺序存储，指的是使用顺序表（数组）存储二叉树。需要注意的是，顺序存储只适用于完全二叉树。换句话说，只有完全二叉树才可以使用顺序表存储。因此，如果我们想顺序存储普通二叉树，需要提前将普通二叉树转化为完全二叉树。
有同学会说，满二叉树也可以使用顺序存储。要知道，满二叉树也是完全二叉树，因为它满足完全二叉树的所有特征。

其实呢也就是将树这种有指向的二维数据 像二维数组一样存在一个线性的 一维的 数据结构中

下面来完成二叉树的顺序存储（一般用于完全二叉树 避免内存浪费）

数组表示的优势和弊端

二叉树同样有两种存储方式，数组和链式存储，对于数组来说，我们利用二叉树的性质然后利用下标可以方便的找到一个节点的子节点和父节点。

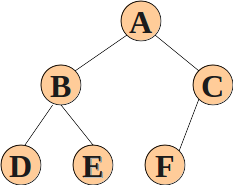
可以在这种完全二叉树中十分方便的找到任何相关联(父子、兄弟等)的元素。

但是由于顺序存储天生适配于完全二叉树，对于下面这种非完全二叉树并不合适，主要体现在空间上的浪费，所以我们需要用到另一种存储方式——链式存储。

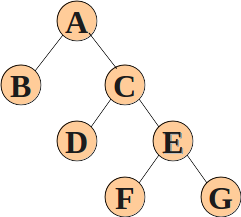
引入链式存储
在链式存储中，每个节点的结构如下

结构描述：一个存储数据的变量与两个指向孩子的指针域。

利用指针域我们便可以完美的存储非完全二叉树，如下：

参考代码

#include <stdio.h>  
  
typedef struct node{ //注意typedef不能省略
    char data;  
    struct node *lchild,*rchild;  
}*BitTree;  
//先序遍历的方式创建二叉树  
void CreatBitTree(BitTree &T) {  
    char c;  
    cin >> c;  
    if (c == '0') T = NULL;  
    else {  
        T = new node;  
        T->data = c;  
        CreatBitTree(T->lchild);  
        CreatBitTree(T->rchild);  
    }  
}  

int main(){  
    BitTree T;  
    CreatBitTree(T);  
    return 0;  
}  

掌握本节内容