二叉树遍历

二叉树的遍历一个重点考查的知识点。

二叉树的遍历是指从二叉树的根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次，且仅被访问一次。

二叉树的访问次序可以分为四种：

前序遍历
中序遍历
后序遍历
层序遍历

前序遍历

前序遍历通俗的说就是从二叉树的根结点出发，当第一次到达结点时就输出结点数据，按照先向左在向右的方向访问。

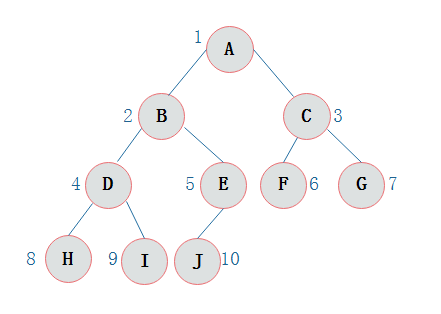
上图所示二叉树访问如下：

从根结点出发，则第一次到达结点A，故输出A;
继续向左访问，第一次访问结点B，故输出B；
按照同样规则，输出D，输出H；
当到达叶子结点H，返回到D，此时已经是第二次到达D，故不在输出D，进而向D右子树访问，D右子树不为空，则访问至I，第一次到达I，则输出I；
I为叶子结点，则返回到D，D左右子树已经访问完毕，则返回到B，进而到B右子树，第一次到达E，故输出E；
向E左子树，故输出J；
按照同样的访问规则，继续输出C、F、G；

则上图所示二叉树的前序遍历输出为：

ABDHIEJCFG

中序遍历

中序遍历就是从二叉树的根结点出发，当第二次到达结点时就输出结点数据，按照先向左在向右的方向访问。

上图所示二叉树中序访问如下：

从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，H；
到达H，H左子树为空，则返回到H，此时第二次访问H，故输出H；
H右子树为空，则返回至D，此时第二次到达D，故输出D；
由D返回至B，第二次到达B，故输出B；
按照同样规则继续访问，输出J、E、A、F、C、G；

则上图所示二叉树的中序遍历输出为：

HDIBJEAFCG

后序遍历

后序遍历就是从二叉树的根结点出发，当第三次到达结点时就输出结点数据，按照先向左在向右的方向访问。

上图所示二叉树后序访问如下：

从根结点出发，则第一次到达结点A，不输出A，继续向左访问，第一次访问结点B，不输出B；继续到达D，H；
到达H，H左子树为空，则返回到H，此时第二次访问H，不输出H；
H右子树为空，则返回至H，此时第三次到达H，故输出H；
由H返回至D，第二次到达D，不输出D；
继续访问至I，I左右子树均为空，故第三次访问I时，输出I；
返回至D，此时第三次到达D，故输出D；
按照同样规则继续访问，输出J、E、B、F、G、C，A；

则上图所示二叉树的后序遍历输出为：

HIDJEBFGCA

层次遍历

层次遍历就是按照树的层次自上而下的遍历二叉树。

针对上图所示二叉树的层次遍历结果为：

ABCDEFGHIJ

遍历常考考点
对于二叉树的遍历有一类典型题型。

1）已知前序遍历序列和中序遍历序列，确定一棵二叉树。
例题：若一棵二叉树的前序遍历为ABCDEF，中序遍历为CBAEDF，请画出这棵二叉树。
分析：前序遍历第一个输出结点为根结点，故A为根结点。早中序遍历中根结点处于左右子树结点中间，故结点A的左子树中结点有CB，右子树中结点有EDF。
如图所示：

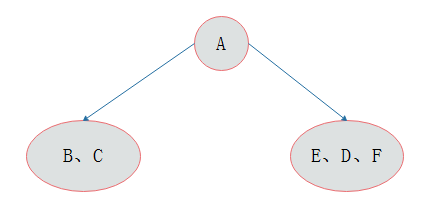
按照同样的分析方法，对A的左右子树进行划分，...

课后练习

【2019年真题】若将一棵树T转化为对应的二又树BT，则下列对BT的遍历中，其遍历序列与T的后根遍历序列相同的是
A. 先序遍历      B. 中序遍历      C. 后序遍历      D. 按层遍历

参考答案：B

【2017年真题】要使一颗非空二叉树的先序序列与中序序列相同，其所有非叶节点须满足的条件是（）
A.只有左子树        B.只有右子树        C.结点的度均为1        D.结点的度均为2

参考答案：B

【2017年真题】已知一颗二叉树的树形如下图所示，其后序序列为e，a，c，b，d，g，f，树中与结点a同层的结点是（）

A.c        B.d        C.f        D.g

参考答案：B

【2015年真题】先序序列为 a,b,c,d 的不同二叉树的个数是（）。
A．13    B．14    C．15    D．16

参考答案：B

【2013年真题】已知三叉树 T 中 6 个叶结点的权分别是 2，3，4，5，6，7，T 的带权（外部）路径长度最小是
 A. 27         B. 46         C. 54         D. 56

参考答案：B
答案解析：利用三叉树的 6 个叶子结点的权构建最小带权生成树，最小的带权路径长度为(2 + 3) * 3 + (4 + 5) * 2 + (6 + 7) * 1 = 46。

【2012年真题】若一棵二叉树的前序遍历序列为 a, e, b, d, c，后序遍历序列为 b, c, d, e, a，则根结点的孩子结点（）
A. 只有 e 
B. 有 e、b 
C. 有 e、c 
D. 无法确定 

参考答案：A
答案解析：考查树的遍历、及由遍历序列确定二叉树的树形。 
前序序列和后序序列不能唯一确定一棵二叉树，但可以确定二叉树中结点的祖先关系：当两个结点 的前序序列为 XY 与后序序列为 YX 时，则 X 为 Y 的祖先。考虑前序序列 a,e,b,d,c、后序序列 b,c,d,e,a， 可知 a 为根结点，e 为 a 的孩子结点；此外，a 的孩子结点的前序序列 e,b,d,c、后序序列 b,c,d,e，可知 e 是 bcd 的祖先，故根结点的孩子结点只有 e。本题答案为 A。

【2011年真题】若一棵二叉树的前序遍历序列和后序遍历序列分别为1,2,3,4和4,3,2,1，则该二叉树的 中序遍历序列不会是（）
A．1,2,3,4 
B．2,3,4,1 C．3,2,4,1
D．4,3,2,1 

解答：C。由前序和后序遍历序列可知3为根结点，故（1,2）为左子树，（4）为右子树， 
C不可能。或画图即可得出结果。 

【2009年真题】给定二叉树如右图所示。设 N 代表二叉树的根，L 代表根结点的左子树，R 代表根结点的右子树。若遍历后的结点序列是 3，1，7，5，6，2，4，则其遍历方式是（）。 

A．LRN         B．NRL         C．RLN         D．RNL

参考答案：D
答案解析：考查平衡二叉树的定义。 
根据平衡二叉树的定义有，任意结点的左右子树高度差的绝对值不超过 1。而其余三个答案均可以找到不符合的结点。

【2017年真题】请设计一个算法，将给定的表示式树（二叉树）转换为等价的中缀表达式（通过括号反映操作符的计算次序）并输出。例如，当下列两颗表达式树作为算法的输入时：

输出的等价中缀表达式分别为(a+b)*(c*(-d))和(a*b)+(-(c-d))。
二叉树结点定义如下：

typedef struct node {    
    char data[10];  //存储操作数或操作符    
    struct node *left, *right;    
}BTree;    

    要求：
（1）给出算法的基本设计思想。
（2）根据设计思想，采用C或C++语言描述算法，关键之处给出注释。

参考答案：
（1）算法的基本设计思想
表达式的中序序列加上必要的括号即为等价的中缀表达式。可以基于二叉树的中序遍历策略得到所需的表达式。
表达式树中分支结点所对应的子表达式的计算次序，由该分支点所处的位置决定。为得到正确的中缀表达式，需要在生成遍历序列的同时，在适当位置增加必要的括号。显然，表达式的最外层（对应根节点）及操作数（对应叶节点）不需要添加括号。
（2）算法实现

void BtreeToE(BTree *root) {  
    BtreeToExp(root, 1);    //根的高度为1  
}  
void BtreeToExp(BTree *root, int deep) {  
    if (root == NULL) return;  
    else if (root->left == NULL && root->right == NULL)  
        //若为叶结点  
        printf("%s", root->data);  
    else {  
        if (deep > 1) printf("("); //若有子表达式则加1层括号  
        BtreeToExp(root->left, deep + 1);  
        printf("%s", root->data);   //输出操作符  
        BtreeToExp(root->right, deep + 1);  
        if (deep > 1) printf(")") //若有子表达式则加1层括号  
    }  
}  

【2014年真题】二叉树的带权路径长度(WPL)是二叉树中所有叶结点的带权路径长度之和。给定一棵二叉树 T，采用二叉链表存储，结点结构为： 

其中叶结点的 weight 域保存该结点的非负权值。设 root 为指向 T 的根结点的指针，请 
设计求 T 的 WPL 的算法，要求： 
1）给出算法的基本设计思想； 
2）使用 C 或 C++语言，给出二叉树结点的数据类型定义； 
3）根据设计思想，采用 C 或 C++语言描述算法，关键之处给出注释。 

参考答案：
考查二叉树的带权路径长度，二叉树的带权路径长度为每个叶子结点的深度与权值之积 
的总和，可以使用先序遍历或层次遍历解决问题。 
1）算法的基本设计思想： 
①基于先序递归遍历的算法思想是用一个 static 变量记录 wpl，把每个结点的深度作为 
递归函数的一个参数传递，算法步骤如下： 
若该结点是叶子结点，那么变量 wpl 加上该结点的深度与权值之积； 
若该结点非叶子结点，那么若左子树不为空，对左子树调用递归算法，若右子树不为空， 
对右子树调用递归算法，深度参数均为本结点的深度参数加一； 
最后返回计算出的 wpl 即可。 
②基于层次遍历的算法思想是使用队列进行层次遍历，并记录当前的层数， 
当遍历到叶子结点时，累计 wpl； 
当遍历到非叶子结点时对该结点的把该结点的子树加入队列； 
当某结点为该层的最后一个结点时，层数自增 1； 
队列空时遍历结束，返回 wpl 
2)二叉树结点的数据类型定义如下： 

typedef struct BiTNode{  
    int weight;  
    struct BiTNode *lchild, *rchild;  
}BiTNode, *BiTree;  

算法代码如下： 
①基于先序遍历的算法： 

int WPL(BiTree root) {  
    return wpl_PreOrder(root, 0);  
}  
int wpl_PreOrder(BiTree root, int deep) {  
    static int wpl = 0; //定义一个 static 变量存储 wpl  
    if(root->lchild == NULL && root->lchild == NULL) //若为叶子结点，累积 wpl  
        wpl += deep*root->weight;  
    if(root->lchild != NULL) //若左子树不空，对左子树递归遍历  
        wpl_PreOrder(root->lchild, deep+1);  
    if(root->rchild != NULL) //若右子树不空，对右子树递归遍历  
        wpl_PreOrder(root->rchild, deep+1);  
    return wpl;  
}  

②基于层次遍历的算法： 

#define MaxSize 100 //设置队列的最大容量  
int wpl_LevelOrder(BiTree root) {  
    BiTree q[MaxSize]; //声明队列，end1 为头指针，end2 为尾指针  
    int end1, end2; //队列最多容纳 MaxSize-1 个元素  
    end1 = end2 = 0; //头指针指向队头元素，尾指针指向队尾的后一个元素  
    int wpl = 0, deep = 0; //初始化 wpl 和深度  
    BiTree lastNode; //lastNode 用来记录当前层的最后一个结点  
    BiTree newlastNode; //newlastNode 用来记录下一层的最后一个结点  
    lastNode = root; //lastNode 初始化为根节点  
    newlastNode = NULL; //newlastNode 初始化为空  
    q[end2++] = root; //根节点入队  
    while(end1 != end2){ //层次遍历，若队列不空则循环  
        BiTree t = q[end1++]; //拿出队列中的头一个元素  
        if(t->lchild == NULL & t->lchild == NULL){  
            wpl += deep*t->weight;  
        } //若为叶子结点，统计 wpl  
        if(t->lchild != NULL){ //若非叶子结点把左结点入队  
            q[end2++] = t->lchild;   
            newlastNode = t->lchild;  
        } //并设下一层的最后一个结点为该结点的左结点  
        if(t->rchild != NULL){//处理叶节点  
            q[end2++] = t->rchild;  
            newlastNode = t->rchild;  
        }  
        if(t == lastNode){ //若该结点为本层最后一个结点，更新 lastNode  
            lastNode = newlastNode;  
            deep += 1; //层数加 1   
        }   
    }  
    return wpl; //返回 wpl  
}