基本概念
平衡二叉树也叫AVL树，它或者是一颗空树，或者具有以下性质的二叉排序树

它的左子树和右子树的高度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。

 

结构
如基本概念所述，它具有一个左子树和一个右子树，且对于任意一个子树而言，左子树和右子树高度只差不超过1.

 

平衡二叉树判别
如下有3棵树，分别判断下哪个是平衡二叉树？

图1：

图2：

图3：

图一，很明显就能看出图1中任何子树的高度差都在没有超过1，

图二，节点25的左子树高度是3，而右子树高度是5，高度差已经超过1；对于节点32而言，左子树高度是3，右子树高度是1，高度差已经超出1，所以该树不是平衡二叉树。

图三，对于节点25的左子树高度是3，而右子树高度是5，高度差已经超过1；对于节点28来说，左子树的高度是0，右指数的高度是2，高度差已经超过1；所以两处不平衡，不是平衡二叉树。

从上图这几个案例，应该能明白什么是平衡二叉树了吧。

首先，平衡二叉树是一个二叉搜索树，其次它每个子树的左右高度差都不超过一。

 

插入详解

对于平衡二叉树而言，当插入的新值导致它不是平衡二叉树了，这该怎么办？

插入新值前：

插入新值后：

如上图，本是平衡的，如果我插入了一个新值是30的节点，那么这棵树的平衡性就会被破坏，它一共破坏了节点32和节点25的平衡性，虽然破坏了2个节点的平衡性，但我们只讨论最近被破坏节点的平衡性（因为底下的处理好了，上面的节点平衡性也会随之处理好），即新插入节点30破坏了节点32的平衡性，因为新插入节点而导致平衡性被破坏的节点也叫麻烦节点，而被其破坏平衡的节点叫被破坏节点。

根据所有结果和经验，一共把破坏平衡型的类型分为了四种，分别是LL型、RR型、LR型和RL型（L=left,R=right）。

LL型
图1：

图2：

图3：

如上图，LL型也为左左型，在被破坏节点的左边的左边插入而导致失衡，则为LL型，注意上面3个图，黑色的线表示它型号判断的路径，所有型号的判断只从被破坏节点开始判断两次，即不管你第三次新插入节点的位置在左还是在右，如图2和图3，一个左一个右，但是都为LL型，因为只判断两次。

LL型解决方案：以被破坏节点为基础进行右旋

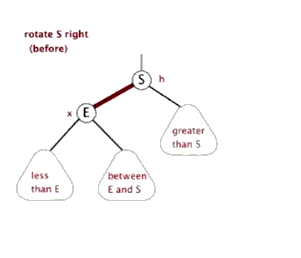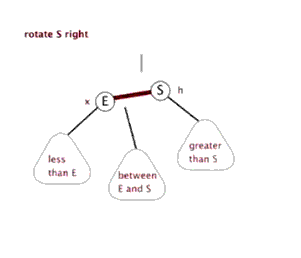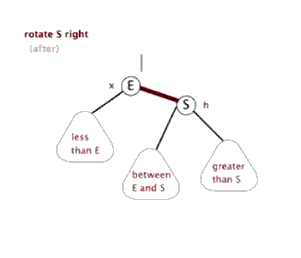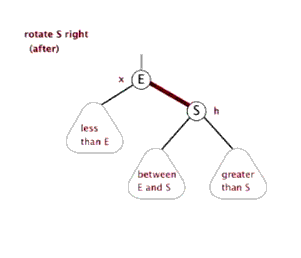
右旋
什么是右旋，根据某个节点向右旋转，只需要记住下面这个图即可，至于右旋为什么能解决LL型问题，其实这是一个经验总结（就像99乘法表），只需要记住即可，后面会总结一个记录方法。

图1右旋：

以25为基础进行进行右旋后结果如下，可以看出，该树处于平衡状态。

图2右旋：

以25为基础进行进行右旋后结果如下，可以看出，该树处于平衡状态。

图3右旋：

以25为基础进行进行右旋后结果如下，可以看出，该树处于平衡状态。

RR型
图1：

图2：

图3：

如上图，RR型也为右右型，在被破坏节点的右边的右边插入而导致失衡，则为RR型，注意上面3个图，黑色的线表示它型号判断的路径，与LL型相反。

LL型解决方案：以被破坏节点为基础进行左旋

 

左旋
什么是左旋，根据某个节点向左旋转，只需要记住下面...

课后习题

 

【2019年真题】在任意一棵非空平衡二又树(AVL树)T1中，删除某结点v之后形成平衡二又树T2，再将w插入T2形成平衡二又树T3。下列关于T1与T3的叙述中，正确的是
I.若v是T1的叶结点，则T1与T3可能不相同
Ⅱ.若v不是T1的叶结点，则T1与T3一定不相同
Ⅲ.若v不是T1的叶结点，则T1与T3一定相同
A.仅I          B. 仅II          C. 仅I、Ⅱ          D. 仅I、Ⅲ

参考答案：A

 

【2015年真题】现有一棵无重复关键字的平衡二叉树（AVL树），对其进行中序遍历可得到一个降序序列。下列关于该平衡二叉树的叙述中，正确的是（）。
A．根结点的度一定为 2    B．树中最小元素一定是叶结点
C．最后插入的元素一定是叶结点    D．树中最大元素一定是无左子树

参考答案：D

 

【2012年真题】若平衡二叉树的高度为 6，且所有非叶结点的平衡因子均为 1，则该平衡二叉树的结点总数为（）。 
A. 10 
B. 20 
C. 32 
D. 33

参考答案：B
答案解析：考查平衡二叉树的最少结点情况。 
所有非叶结点的平衡因子均为 1，即平衡二叉树满足平衡的最少结点情况，如图 xxx 所示。画图时， 先画出 T1 和 T2；然后新建一个根结点，连接 T2、T1 构成 T3；新建一个根结点，连接 T3、T2 构成 T4；„„ 依此类推，直到画出 T6，可知 T6 的结点数为 20。对于高度为 N 的题述的平衡二叉树，它的左、右子树分别为高度为 N-1 和 N-2 的所有非叶结点的平衡因子均为 1 的平衡二叉树。二叉树的结点总数公式为： 
CN=CN-1+CN-2+1，C2=2，C3=4，递推可得 C6=20。 
【排除法】 对于选项 A，高度为 6、结点数为 10 的树怎么也无法达到平衡。对于选项 C，接点较多时，考虑较极端情形，即第 6 层只有最左叶子的完全二叉树刚好有 32 个结点，虽然满足平衡的条件，但显然再删去部分结点，依然不影响平衡，不是最少结点的情况。同理 D 错误。只可能选 B。

 

【2010年真题】在右图所示的平衡二叉树中，插入关键字 48 后得到一棵新平衡二叉树。在新平衡二叉树中，关键字 37 所在结点的左、右子结点中保存的关键字分别是（）

A．13，48 
B．24，48 
C．24，53 
D、24，90 

参考答案：C
答案解析：考查平衡二叉树的插入算法。 
插入 48 以后，该二叉树根结点的平衡因子由-1 变为-2，失去平衡，需进行两次旋转（先右旋后左旋）操作。