AOE网和AOV网
上一篇的拓扑排序中提到了AOV网(Activity On Vertex Network),与之相对应的是AOE网(Activity on edge network),即边表示活动的网。
AOV用顶点表示活动的网,描述活动之间的制约关系。
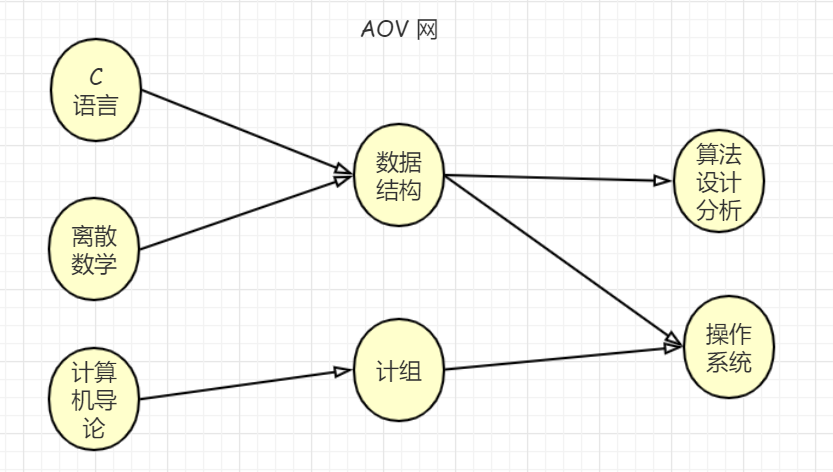
AOE是带权值的有向图,以顶点表示事件,以边表示活动,边上的权值表示活动的开销(如项目工期)。AOE 是建立在子过程之间的制约关系没有矛盾的基础之上,再来分析整个过程需要的开销。所以如果给定AOV网中各顶点活动所需要的时间,则可以转换为AOE网,较为简单的方法就是把每个顶点都拆分成两个顶点,分别表示活动的起点和终点
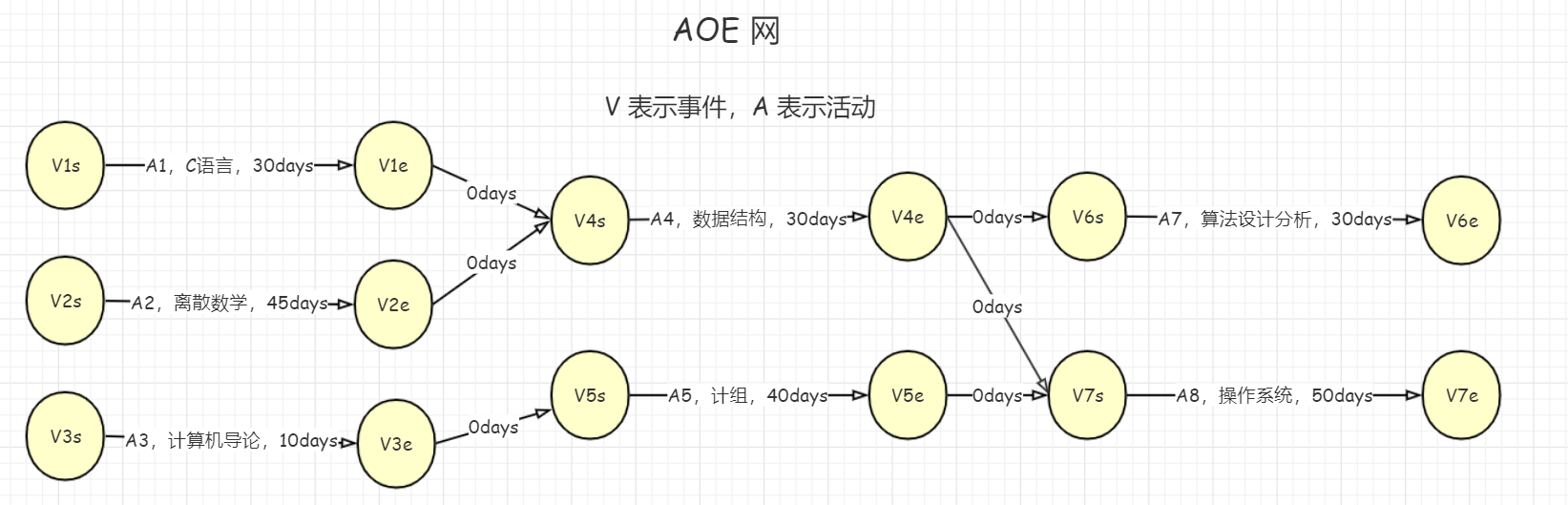
事件和活动
把上图转换成一般的AOE图如下
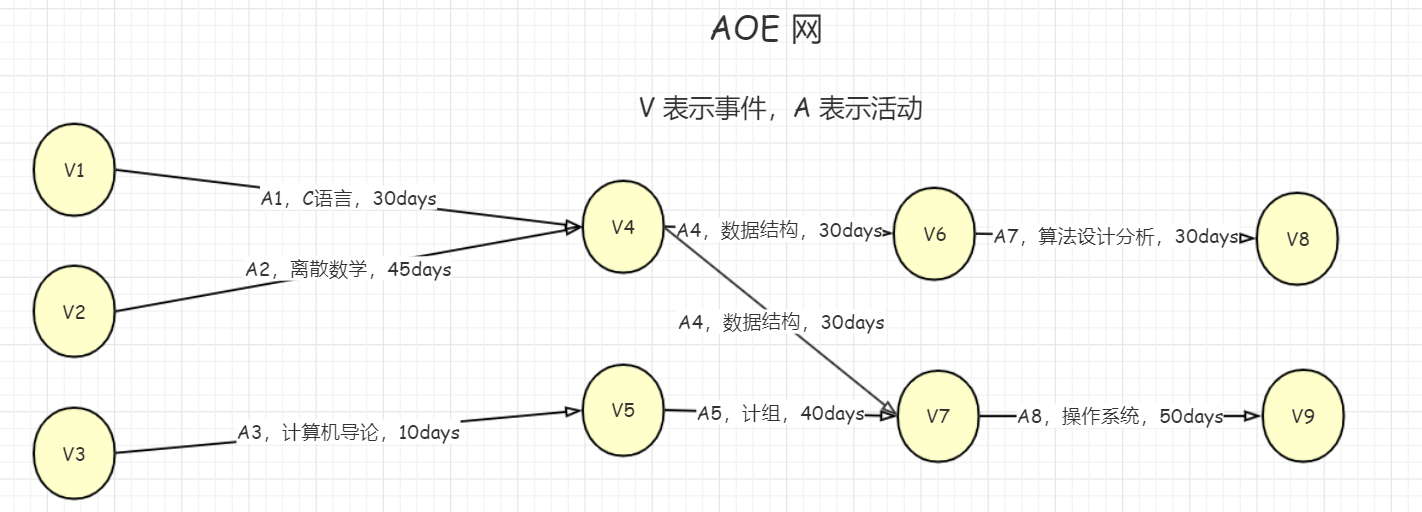
“活动”表示学习课程的过程,而“事件”表示的是一个时间点或者说一种状态(自己的理解),开始和完成活动是一个事件,比如:V4表示学完C语言。而这个事件同时也代表这前面的课程都已经学完了,可以开始学后面的课程了。
关键路径
AOE一般用来估算工程的完成时间。AOE表示工程的流程,把没有入边的称为始点或者源点,没有出边的顶点称为终点或者汇点。一般情况下,AOE只有一个源点一个汇点。但上面用的例图就不止一个,如果碰到这种情况,就可以再加一个“超级源(终)点”,连接所有入(出)度为0的点(不加也不会影响最后的答案)。
关键路径:从源点到汇点具有最长路径(强调:就是AOE网中权值和最大的路径),在关键路径上的活动叫关键活动。但为什么是最大长度呢?
关键路径是AOE网中的最长路径,也是整个工程的最短完成时间,如何理解此处的“最长”和“最短”呢?比如我们想要把“算法设计分析”学完,那么需要的时间就是max(A1,A2)+(A4)+(A7)=105days,那么这105days是最长路径,也是整个工程的最短完成时间,如果我们试图缩短学习的时间,那么缩短“C语言”课程的学习时间显然是没有用的。只有缩短关键路径上的关键活动时间才可以减少整个项目的时间。比如让“离散数学”的时间缩短为30days,则总时间就会减少为90days。
来看四个定义(活动是一个过程,用“开始”,事件是一个时间点,用“发生”):
活动的最早开始时间 ETE(earliest time of edge):所有前导活动都完成,可以开始的时间。
活动的最晚开始时间 LTE(latest time of edge):不推迟工期的最晚开工时间。
事件的最早发生时间 ETV(earliest time of vertex):可以等价理解为旧活动的最早结束时间 或 新活动的最早开始时间
事件的最晚发生时间 LTV(latest time of vertex):可以等价理解为就活动的最晚结束时间 或 新活动的最晚开始时间
举例说明一下,“数据结构”课程的活动最早开始时间就是“离散数学”学完,45days。对于“C语言”课程来说,需要30days,而“离散数学”需要45days,那么&...
课后习题
【2019年真题】下图所示的AOE网表示一项包含8个活动的工程。活动d的最早开始时间和最迟开始时间分别是

A.3和7 B. 12和12 C. 12和14 D. 15和15
参考答案:C
【2013年真题】下列 AOE 网表示一项包含 8 个活动的工程。通过同时加快若干活动的进度可以缩短整个工程的工期。下列选项中,加快其进度就可以缩短工程工期的是()

A.c 和 e B. d 和 e C. f 和 d D. f 和 h
参考答案:C
答案解析:根据 AOE 网的定义可知,关键路径上的活动时间同时减少,可以缩短工期。
【2011年真题】已知有 6 个顶点(顶点编号为 0~5)的有向带权图 G,其邻接矩阵 A 为上三角矩阵,按行为主序(行优先)保存在如下的一维数组中。

要求:
(1)写出图 G 的邻接矩阵 A。
(2)画出有向带权图 G。
(3)求图 G 的关键路径,并计算该关键路径的长度。
解答:
(1)图 G 的邻接矩阵 A 如下所示。
(2)有向带权图 G 如下图所示。
(3)关键路径为 01235(如下图所示粗线表示),长度为 4+5+4+3=16





 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1



登录后开始许愿
暂无评论,来抢沙发