有向无环图(DAG)
如果一个有向图不存在环,也就是任意结点都无法通过一些有向边回到自身,那么称这个有向图为有向无环图。
AOV网络
在有向图中,用顶点表示活动,用有向边<Vi,Vj>表示活动 i 是活动 j 的必须条件。这种有向图称为用顶点表示活动的网络(Active on vertices),简称AOV网络。
在AOV网络中,如果活动Vi必须在Vj之前进行,则存在有向边<Vi,Vj>,并称Vi是Vj的直接前驱,Vj是Vi的直接后继。这种前驱与后继的关系具有传递性和反自反性,这要求AOV网络中不能出现回路,即有向环。因此,对于给定的AOV网络,必须先判断它是否存在有向环。
拓扑排序
检测有向环可以通过对AOV网络进行拓扑排序,该过程将各个顶点排列成一个线性有序的序列,使得AOV网络中所有的前驱和后继关系都能得到满足。 如果拓扑排序能够将AOV网络的所有顶点都排入一个拓扑有序的序列中,则说明该AOV网络中没有有向环,否则AOV网络中必然存在有向环。AOV网络的顶点的拓扑有序序列不唯一。可以将拓扑排序看做是将图中的所有节点在一条水平线上的展开,图的所有边都从左指向右。
用计算机专业的几门课程的学习次序来描述拓扑关系(打个比方,图内容可能不是特别严谨) ,显然对于一门课来说,必须先学习它的先导课程才能更好地学习这门课程,比如学数据结构必须先学习C语言和离散数学,而且先导课程中不能有环,否则没有尽头了
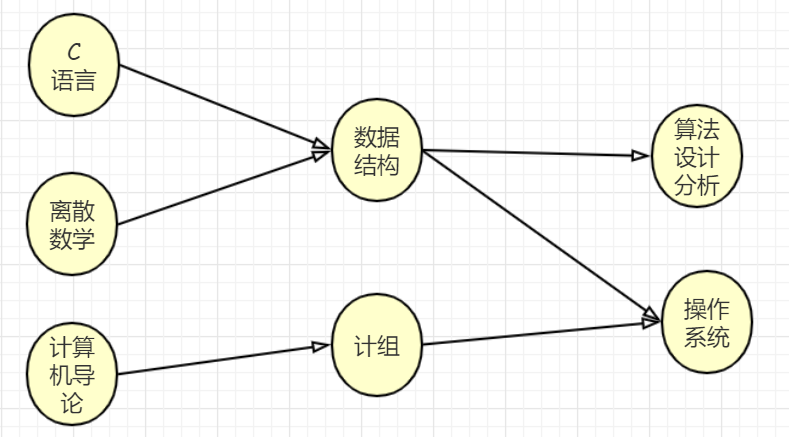
而且还可以发现,如果两门课程之间没有直接或间接的先导关系,那么这两门课的学习先后是任意的(比如“C语言”和“离散数学”的学习顺序就是任意的),于是上述课程就可以排成一个水平展开的先后顺序,如下图

拓扑排序的结果不唯一,比如“C语言”和“离散数学”就可以换下顺序,又或者把“计算机导论”向前放在任何一个位置都可以。总结一下就是,如果某一门课没有先导课程或是所有的先导课程都已经学习完毕,那么这门课就可以学习了。如果同时有多门这样的课,它们的学习顺序任意。
算法描述
对于一个有向无环图
(1)统计所有节点的入度,对于入度为0的节点就可以分离出来,然后把这个节点指向所有的节点的入度−1。
(2)重复(1),直到所有的节点都被分离出来,拓扑排序结束。
(3)如果最后不存在入度为0的节点,那就说明有环,无解。
解释一下,假设A为一个入度为0的结点,就表示A结点没有前驱结点,可以直接做,把A完成后,对于A的所有后继结点来说,前驱结点就完成了一个,入度进行−1。

时间复杂度
如果AOV网络有n个顶点,e条边,在拓扑排序的过程中,搜索入度为零的顶点所需的时间是O(n)。在正常情况下,每个顶点进一次栈,出一次栈,所需时间O(n)。每个顶点入度减1的运算共执行了e次。所以总的时间复杂为O(n+e)。
因为拓扑排序的结果不唯一,所以题目一般会要求按某种顺序输出,就需要使用优先级队列,这里采取了最小字典序输出。
参考代码
const int maxn = 505;
bool mpt[maxn][maxn]; //邻结矩阵存储图
int...
课后习题
【2018年真题】下列选项中,不是如下有向图的拓扑序列的是()

A. 1, 5, 2, 3, 6, 4 B. 5, 1, 2, 6, 3, 4
C. 5, 1, 2, 3, 6, 4 D. 5, 2, 1, 6, 3, 4
参考答案:D
【2016年真题】若将n个顶点e条弧的有向图采用邻接表存储,则拓扑排序算法的时间复杂度是()
A.O(n) B.O(n+e) C.O(n2) D.O(n*e)
参考答案:B
【2014年真题】对如下所示的有向图进行拓扑排序,得到的拓扑序列可能是()

A.3,1,2,4,5,6
B.3,1,2,4,6,5
C.3,1,4,2,5,6
D.3,1,4,2,6,5
参考答案:D
答案解析:按照拓扑排序的算法,每次都选择入度为 0 的结点从图中删去,此图中一开始只有 结点 3 的入度为 0;删掉 3 结点后,只有结点 1 的入度为 0;删掉结点 1 后,只有结点 4 的 入度为 0;删掉 4 结点后,结点 2 和结点 6 的入度都为 0,此时选择删去不同的结点,会得出不同的拓扑序列,分别处理完毕后可知可能的拓扑序列为 314265 和 314625,选 D。
【2012年真题】若用邻接矩阵存储有向图,矩阵中主对角线以下的元素均为零,则关于该图拓扑序列的结论是()。
A.存在,且唯一
B.存在,且不唯一
C.存在,可能不唯一
D.无法确定是否存在
参考答案:C
答案解析:考查拓扑排序、与存储结构和图性质的关系。
对角线以下元素均为零,表明该有向图是一个无环图,因此一定存在拓扑序列。对于拓扑序列是否 唯一,我们试举一例:设有向图的邻接矩阵
,则存在两个拓扑序列。所以该图存在可能不唯一的拓扑排序。
结论:对于任一有向图,如果它的邻接矩阵中对角线以下(或以上)的元素均为零,则存在拓扑序列(可能不唯一)。反正,若图存在拓扑序列,却不一定能满足邻接矩阵中主对角线以下的元素均为零,但是可以通过适当地调整结点编号,使其邻接矩阵满足前述性质。
【2011年真题】下列关于图的叙述中,正确的是()
Ⅰ. 回路是简单路径
Ⅱ.存储稀疏图,用邻接矩阵比邻接表更省空间
Ⅲ.若有向图中存在拓扑序列,则该图不存在回路
A.仅Ⅱ
B.仅Ⅰ、Ⅱ
C.仅Ⅲ
D.仅Ⅰ、Ⅲ
解答:C。Ⅰ.回路对应于路径,简单回路对应于简单路径;Ⅱ.刚好相反;Ⅲ.拓扑有序的必要条件。故选C。
【2010年真题】对下图进行拓扑排序,可以得到不同的拓扑序列的个数是()。

A.4 B. 3 C.2 D.1
参考答案:B
答案解析:考查拓扑排序序列。
题中图有三个不同的拓扑排序序列,分别为 abced,abecd,aebcd。


 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1



登录后开始许愿
暂无评论,来抢沙发