返回主页
(10分)AOE网,描述12个工程活动及持续时间
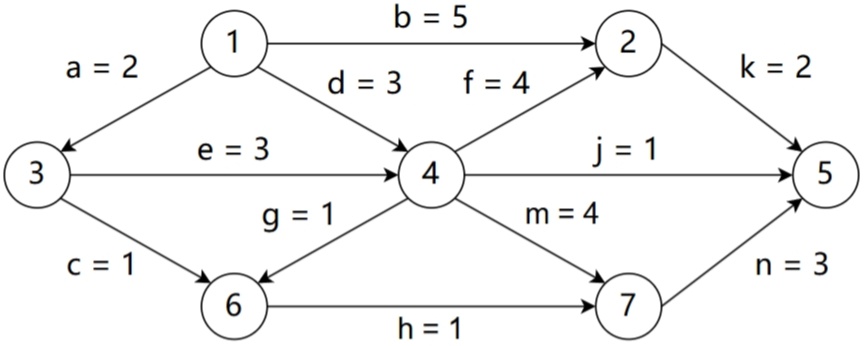
(1)完成该工程的最短时间是多少?哪些是关键活动?(4分)
(2)若以最短时间完成工程,则与活动e同时进行的活动可能有哪些?(2分)
(3)时间余量最大的活动是哪个?其时间余量是多少?(2分)
(4)假设工程从时刻0启动,因某种原因,活动b在时刻6开始,为保证工程不延期,在其它活动持续时间保持不变的情况下, b的持续时间最多是多少?若不改变b的持续时间,则压缩哪个活动的持续时间也能保证工程不延期?(2分)
回答区域
提示
提示内容

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1



登录后提交答案