本题为一道简单难度的考察搜索的算法题，考研只需要掌握深度优先搜索和广度优先搜索即可。
这道题要注意的是题目要求“二叉树中所有叶结点的带权路径长度之和”，也就是只有“叶结点”才需要计算WPL。
构造测试用例如下图所示：
方法一：深度优先搜索
C代码如下（含测试用例）：
#include <stdio.h>
#include <stdlib.h>
struct TreeNode {
int weight;
struct TreeNode *left;
struct TreeNode *right;
};
int dfs(struct TreeNode* root, int depth) {
if (root == NULL) {
return 0;
}
if (root->left == NULL && root->right == NULL) {
return root->weight * depth;
}
return dfs(root->left, depth + 1) + dfs(root->right, depth + 1);
}
int pathSum(struct TreeNode* root) {
return dfs(root, 0);
}
struct TreeNode *createBinaryTree(int *a, int n) {
if (a[0] == -1) {
return NULL;
}
int i = 0;
struct TreeNode *root = (struct TreeNode *)malloc(sizeof(struct TreeNode));
root->weight = a[i++];
root->left = NULL;
root->right = NULL;
struct TreeNode** que = (struct TreeNode**)malloc(sizeof(struct TreeNode*));
int front = 0, rear = 0;
struct TreeNode *curr = root;
que[rear++] = curr;
while (front < rear && i < n) {
curr = que[front++];
for (int j = 0; j < 2 && i < n; j++, i++) {
if (a[i] != -1) {
if (j == 0) {
curr->left = (struct TreeNode *)malloc(sizeof(struct TreeNode));
curr->left->weight = a[i];
curr->left->left = NULL;
curr->left->right = NULL;
que[rear++] = curr->left;
} else {
curr->right = (struct TreeNode *)malloc(sizeof(struct TreeNode));
curr->right->weight = a[i];
curr->right->left = NULL;
curr->right->right = NULL;
que[rear++] = curr->right;
}
}
}
}
return root;
}
int main() {
int W[] = {1, -1, 2, 3};
printf("%d", pathSum(createBinaryTree(W, 4)));
return 0;
}
C++代码如下（含测试用例）：
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct TreeNode {
int weight;
TreeNode *left;
TreeNode *right;
TreeNode() : weight(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : weight(x), left(nullptr), right(nullptr) {}
};
int dfs(TreeNode* root, int depth) {
if (root == nullptr) {
return 0;
}
if (root->left == nullptr && root->right == nullptr) {
return root->weight * depth;
}
return dfs(root->left, depth + 1) + dfs(root->right, depth + 1);
}
int pathSum(TreeNode* root) {
return dfs(root, 0);
}
TreeNode *createBinaryTree(vector<int> weights) {
if (weights[0] == -1) {
return nullptr;
}
const int n = weights.size();
int i = 0;
TreeNode *root = new TreeNode(weights[i++]);
queue<TreeNode *> Q;
Q.push(root);
while (!Q.empty() && i < n) {
TreeNode *node = Q.front();
Q.pop();
for (int j = 0; j < 2 && i < n; j++, i++) {
if (weights[i] != -1) {
if (j == 0) {
node->left = new TreeNode(weights[i]);
Q.push(node->left);
} else {
node->right = new TreeNode(weights[i]);
Q.push(node->right);
}
}
}
}
return root;
}
int main() {
vector<int> W = {1, -1, 2, 3};
cout << pathSum(createBinaryTree(W));
return 0;
}
复杂度分析
- 时间复杂度： O(n) ，其中 n 是二叉树的结点数。
- 空间复杂度： O(n) ，为递归过程中栈的开销，平均情况下为 O(logn) ，最坏情况下树呈现链状，为 O(n) 。
方法二：广度优先搜索
C代码如下（含测试用例）：
#include <stdio.h>
#include <stdlib.h>
struct TreeNode {
int weight;
struct TreeNode *left;
struct TreeNode *right;
};
int pathSum(struct TreeNode* root) {
if (root == NULL) {
return 0;
}
struct TreeNode *curr = root;
struct TreeNode** que = (struct TreeNode**)malloc(sizeof(struct TreeNode*));
int front = 0, rear = 0;
que[rear++] = curr;
int wpl = 0;
int depth = 0;
while (front < rear) {
int sz = rear - front;
while (sz > 0) {
curr = que[front++];
if (curr->left == NULL && curr->right == NULL) {
wpl += curr->weight * depth;
}
if (curr->left) {
que[rear++] = curr->left;
}
if (curr->right) {
que[rear++] = curr->right;
}
sz--;
}
depth++;
}
return wpl;
}
struct TreeNode *createBinaryTree(int *a, int n) {
if (a[0] == -1) {
return NULL;
}
int i = 0;
struct TreeNode *root = (struct TreeNode *)malloc(sizeof(struct TreeNode));
root->weight = a[i++];
root->left = NULL;
root->right = NULL;
struct TreeNode** que = (struct TreeNode**)malloc(sizeof(struct TreeNode*));
int front = 0, rear = 0;
struct TreeNode *curr = root;
que[rear++] = curr;
while (front < rear && i < n) {
curr = que[front++];
for (int j = 0; j < 2 && i < n; j++, i++) {
if (a[i] != -1) {
if (j == 0) {
curr->left = (struct TreeNode *)malloc(sizeof(struct TreeNode));
curr->left->weight = a[i];
curr->left->left = NULL;
curr->left->right = NULL;
que[rear++] = curr->left;
} else {
curr->right = (struct TreeNode *)malloc(sizeof(struct TreeNode));
curr->right->weight = a[i];
curr->right->left = NULL;
curr->right->right = NULL;
que[rear++] = curr->right;
}
}
}
}
return root;
}
int main() {
int W[] = {1, -1, 2, 3};
printf("%d", pathSum(createBinaryTree(W, 4)));
return 0;
}
C++代码如下（含测试用例）：
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct TreeNode {
int weight;
TreeNode *left;
TreeNode *right;
TreeNode() : weight(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : weight(x), left(nullptr), right(nullptr) {}
};
int pathSum(TreeNode* root) {
if (root == nullptr) {
return 0;
}
queue<TreeNode *>Q;
TreeNode *curr = root;
Q.push(curr);
int wpl = 0;
int depth = 0;
while (!Q.empty()) {
int sz = (int)Q.size();
while (sz > 0) {
curr = Q.front();
Q.pop();
if (curr->left == nullptr && curr->right == nullptr) {
wpl += curr->weight * depth;
}
if (curr->left) {
Q.push(curr->left);
}
if (curr->right) {
Q.push(curr->right);
}
sz--;
}
depth++;
}
return wpl;
}
TreeNode *createBinaryTree(vector<int> weights) {
if (weights[0] == -1) {
return nullptr;
}
const int n = weights.size();
int i = 0;
TreeNode *root = new TreeNode(weights[i++]);
queue<TreeNode *> Q;
Q.push(root);
while (!Q.empty() && i < n) {
TreeNode *node = Q.front();
Q.pop();
for (int j = 0; j < 2 && i < n; j++, i++) {
if (weights[i] != -1) {
if (j == 0) {
node->left = new TreeNode(weights[i]);
Q.push(node->left);
} else {
node->right = new TreeNode(weights[i]);
Q.push(node->right);
}
}
}
}
return root;
}
int main() {
vector<int> W = {1, -1, 2, 3};
cout << pathSum(createBinaryTree(W));
return 0;
}
复杂度分析
- 时间复杂度： O(n) ，其中 n 是二叉树的结点数。
- 空间复杂度： O(n) ，队列中的元素不超过 n 个。
。
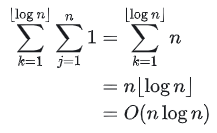
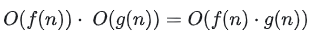
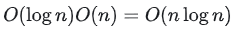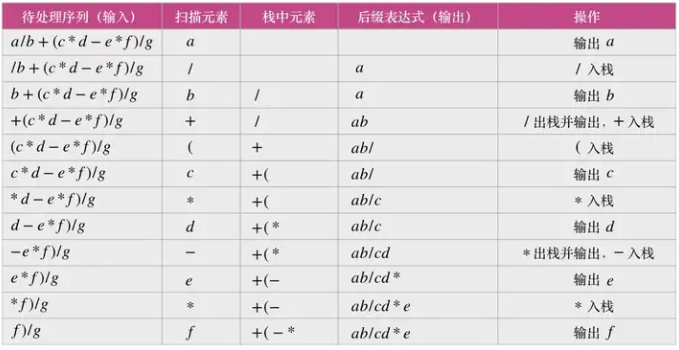
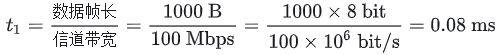，传播时延为 50 ms ，主机乙发送一个确认帧的时延为 t2 ，因为乙每收到一个数据帧立即利用一个短帧（忽略其传输延迟）进行确认，所以 t2=0 ，传播时延为 50 ms 。一个周期 T=0.08 ms+50 ms+0 ms+50 ms=100.08 ms 。因为数据链路层采用后退 N 帧协议 (GBN) 传输数据，为使信道利用率达到最高，在一个周期内，发送方可以连续发送多个数据帧，将位于发送窗口中的帧全部发送出去。甲的发送窗口尺寸为1000，1000个帧的发送时延为 1000t1=80 ms<T ，满足要求。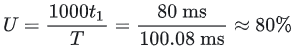
The road of your choice, you have to go on !
粤ICP备16082171号-1
