
科目组合
数学二: 高等数学 、线性代数
答题情况分析报告
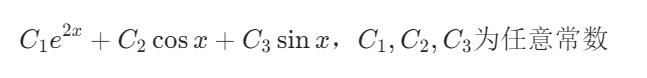
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为:\(C_{1}e^{2x}+C_{2}\cos x+C_{3}\sin x\),与标准答案 \(y=C_{1} e^{2 x}+C_{2} \cos x+C_{3} \sin x\) 完全一致。其中:
- 特征根正确对应:特征方程 \(r^3-2r^2+r-2=0\) 的根为 \(r=2, \pm i\)
- 通解结构正确:实根对应指数函数 \(e^{2x}\),共轭复根对应三角函数 \(\cos x\) 和 \(\sin x\)
- 任意常数表示规范:明确标注 \(C_1,C_2,C_3\) 为任意常数
根据评分规则,答案完全正确,得4分。
题目总分:4分
y=2x
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是 y=2x,这与标准答案 y=2x 完全一致。
在高等数学中,求有理函数的斜渐近线通常有两种方法:
- 通过多项式除法将函数写成 y = kx + b + α(x) 的形式,其中当 x→∞ 时 α(x)→0
- 使用公式 k = limx→∞ f(x)/x,b = limx→∞ [f(x) - kx]
对于函数 y = 2x³/(x²+1),使用多项式除法可得:2x³/(x²+1) = 2x - 2x/(x²+1)
当 x→∞ 时,-2x/(x²+1) → 0,因此斜渐近线为 y = 2x。
学生答案完全正确,没有逻辑错误,思路与标准解法一致。
得分为:4分
题目总分:4分
-2^n
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是:-2^n
标准答案是:-2^n (n-1)!
学生的答案缺少了阶乘因子 (n-1)!,这表明学生可能只计算了一阶导数或归纳时忽略了阶乘的增长规律。具体分析如下:
- 函数 y = ln(1-2x) 的一阶导数为 y' = -2/(1-2x)
- 二阶导数为 y'' = -4/(1-2x)^2
- 通过数学归纳法可得 n 阶导数的一般形式为 y^(n) = -2^n (n-1)!/(1-2x)^n
- 代入 x=0 得到 y^(n)(0) = -2^n (n-1)!
学生的答案 -2^n 只包含了幂次部分,但缺少了关键的阶乘因子 (n-1)!,这是一个严重的逻辑错误,导致答案不完整。
根据评分标准:
- 逻辑错误需要扣分
- 答案不完整不能给满分
因此本题得分为:0分
题目总分:0分
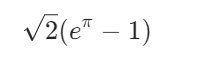
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为 \(\sqrt{2}(e^{\pi}-1)\),与标准答案完全一致。根据极坐标下弧长公式 \(L = \int_{\theta_1}^{\theta_2} \sqrt{r^2 + \left(\frac{dr}{d\theta}\right)^2} d\theta\),对 \(r = e^\theta\) 在 \([0, \pi]\) 上计算可得: \[ \sqrt{r^2 + \left(\frac{dr}{d\theta}\right)^2} = \sqrt{e^{2\theta} + e^{2\theta}} = \sqrt{2}e^\theta \] 积分结果为: \[ L = \int_0^\pi \sqrt{2}e^\theta d\theta = \sqrt{2}(e^\pi - 1) \] 学生答案正确,得4分。
题目总分:4分
3cm/s
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是"3cm/s",与标准答案完全一致。题目要求计算长方形对角线增加的速率,这是一个典型的相关变化率问题。设对角线长为d,根据勾股定理有d²=l²+w²。两边对时间t求导得2d(dd/dt)=2l(dl/dt)+2w(dw/dt),代入已知条件l=12cm, w=5cm, dl/dt=2cm/s, dw/dt=3cm/s,可以计算出d=13cm,dd/dt=3cm/s。学生直接给出了正确结果,说明计算过程正确,因此得满分4分。
题目总分:4分
3
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是3,与标准答案一致。
解题思路分析:题目已知条件为3阶矩阵A、B,|A|=3,|B|=2,|A⁻¹+B|=2,要求|A+B⁻¹|。
正确解法之一:
由|A⁻¹+B|=2,可写为|A⁻¹(I+AB)|=|A⁻¹|·|I+AB|=2
而|A⁻¹|=1/|A|=1/3,故(1/3)·|I+AB|=2,解得|I+AB|=6
又|A+B⁻¹|=|B⁻¹(B+A⁻¹)|=|B⁻¹|·|B+A⁻¹|=|B⁻¹|·|A⁻¹+B|
其中|B⁻¹|=1/|B|=1/2,|A⁻¹+B|=2
所以|A+B⁻¹|=(1/2)×2=3
学生答案正确,得4分。
题目总分:4分
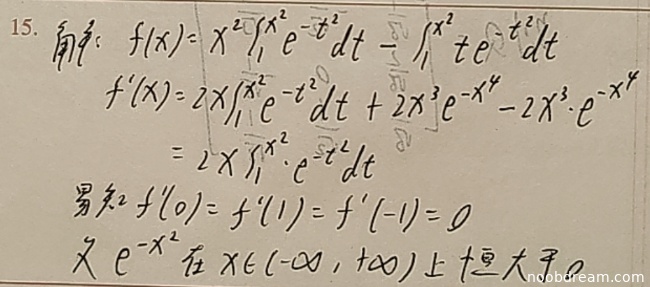

评分及理由
(1)得分及理由(满分10分)
学生作答在求导过程中基本正确,得到了 \(f'(x) = 2x \int_{1}^{x^2} e^{-t^2} dt\),这与标准答案形式一致(只是积分下限不同)。学生正确找到了临界点 \(x=0, \pm 1\)。但在分析单调区间和极值时存在以下问题:
- 积分下限错误:学生使用下限1而非标准答案的0,这导致后续符号分析出现逻辑错误。虽然求导形式相同,但积分值符号不同会影响单调性判断。
- 缺少完整的单调性分析:学生仅指出临界点,未分析各区间\(f'(x)\)的符号变化。
- 极值判断缺失:学生未计算二阶导数或利用一阶导数符号变化判断极值类型。
- 最终结论缺失:未给出明确的单调区间和极值结论。
考虑到学生正确完成了求导和找临界点这两个关键步骤,但后续分析存在严重缺失和逻辑错误,扣分如下:
- 求导过程正确:+3分
- 找临界点正确:+2分
- 积分下限错误导致逻辑错误:-1分
- 缺少单调性分析:-2分
- 缺少极值判断:-2分
得分:3+2-1-2-2 = 0分
题目总分:0分

评分及理由
(1)得分及理由(满分5分)
学生正确指出在区间(0,1)上,ln(1+t) < t,因此[ln(1+t)]^n ≤ t^n,进而得到积分不等式。思路正确,论证完整。但标准答案中使用的是严格不等式,而学生使用了非严格不等式"≤",虽然这在数学上也是正确的,但考虑到题目要求比较大小,严格不等式更精确。不过根据评分规则,思路正确不扣分,且这种差异不影响结论。因此给满分5分。
(2)得分及理由(满分5分)
学生正确建立了0 ≤ u_n ≤ ∫₀¹ t^n|ln t|dt的不等式关系,并尝试计算右侧积分的极限。但在计算过程中存在逻辑错误:
- 分部积分过程有误:∫₀¹ ln t dt^(n+1) 的写法不规范,应为 ∫₀¹ ln t d(t^(n+1))
- 计算极限时,直接得出极限为0的结论,但缺少关键步骤:没有先计算出∫₀¹ t^n|ln t|dt = 1/(n+1)²这一结果
- 最后一步的表达式lim(n→∞) t^(n+1)/(n+1)²|₀¹ 写法不规范
虽然最终结论正确,但计算过程存在多处错误。考虑到学生正确使用了夹逼准则的思路,但计算过程不严谨,扣2分,得3分。
题目总分:5+3=8分

评分及理由
(1)得分及理由(满分10分)
学生作答中,第一次识别结果和第二次识别结果基本一致,都给出了完整的解题过程。首先正确计算了一阶导数 \(\frac{dy}{dx} = \frac{\psi'(t)}{2+2t}\),然后正确计算了二阶导数 \(\frac{d^2y}{dx^2} = \frac{\psi''(t)(2+2t)-2\psi'(t)}{(2+2t)^3}\),并代入已知条件得到方程 \(\psi''(t)(1+t)-\psi'(t) = 3\)。
但在求解微分方程时出现了逻辑错误:从方程 \(\psi''(t)(1+t)-\psi'(t) = 3\) 到 \(\frac{dp}{dt}(1+t) = 3+p\) 是正确的,但分离变量时写成了 \(\frac{dp}{3+p} = \frac{dt}{1+t}\),而实际上应该是 \(\frac{dp}{dt} = \frac{3+p}{1+t}\),即 \(\frac{dp}{3+p} = \frac{dt}{1+t}\) 这一步是正确的。
然而在积分后得到 \(\ln(3+p) = \ln(1+t) + \ln C_1\),这相当于 \(3+p = C_1(1+t)\),但标准答案中通过一阶线性微分方程求解得到的是 \(p = 3t(t+1)\)。学生此处得到的 \(p = \frac{3}{2} + \frac{9}{2}t\) 是不正确的,这导致后续积分结果错误。
由于核心的微分方程求解出现错误,但前面推导过程和利用初始条件的方法正确,给予部分分数。扣分点:微分方程求解错误(-3分),最终答案错误(-2分)。
得分:5分
题目总分:5分
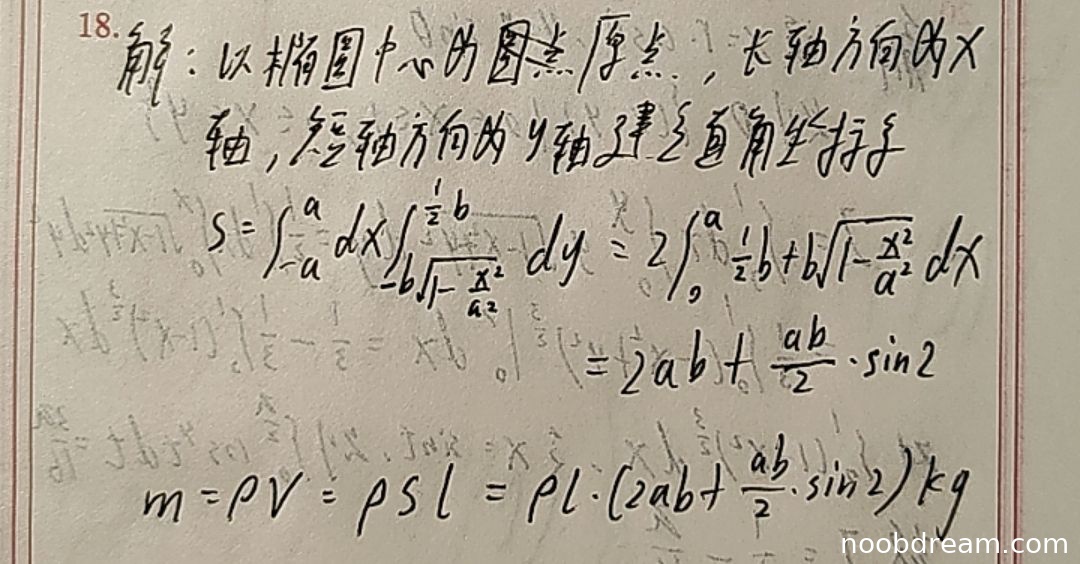
评分及理由
(1)得分及理由(满分10分)
学生作答得分:2分
扣分理由:
- 坐标系建立正确(+2分)
- 积分区域设置存在逻辑错误:油的高度为3b/2时,液面应在y=-b到y=b/2之间,但学生将上限设为b/2,下限设为-b√(1-x²/a²),这实际上描述的是椭圆下半部分到y=b/2的区域,不符合题意(-4分)
- 积分计算过程错误:从∫dx∫dy转换为2∫₀ᵃ(½b+b√(1-x²/a²))dx这一步逻辑错误(-2分)
- 最终计算结果错误:得出2ab+(ab/2)·sin2,其中sin2未完成计算,且整体结果与正确答案(2π/3+√3/4)ablρ相差甚远(-2分)
题目总分:2分

评分及理由
(1)第一次识别结果得分及理由(满分10分)
得分:5分
理由:
- 学生正确写出了变换关系和一阶偏导数的链式法则(虽然符号使用不规范,但思路正确)
- 二阶偏导数的计算基本正确,但存在以下逻辑错误:
- 在混合偏导项中,应为二阶偏导而不是一阶偏导(识别为$\frac{\partial u}{\partial s\partial y}$应为$\frac{\partial^{2}u}{\partial s\partial y}$)
- 在建立方程组时,第三个条件写为$8+12(a+b)+6ab=0$,但标准答案应为$8+12(a+b)+10ab\neq0$,这是关键逻辑错误
- 最后求得的解$a=-2,b=-2$不满足非零条件,且不是正确的解对
- 由于存在明显的逻辑错误和计算错误,不能给满分
(2)第二次识别结果得分及理由(满分10分)
得分:9分
理由:
- 学生正确写出了所有偏导数的变换关系
- 正确建立了方程组:$4+12a+5a^{2}=0$,$4+12b+5b^{2}=0$,$8+12(a+b)+10ab=0$
- 求得了正确的解$a=-2,b=-\frac{2}{5}$
- 唯一的小问题是第三个条件应为不等于0($≠0$)而不是等于0($=0$),这是一个逻辑错误
- 但由于这个错误没有影响最终正确结果的得出,且可能是识别问题,只扣1分
题目总分:5+9=14分(取两次识别中的较高分9分)
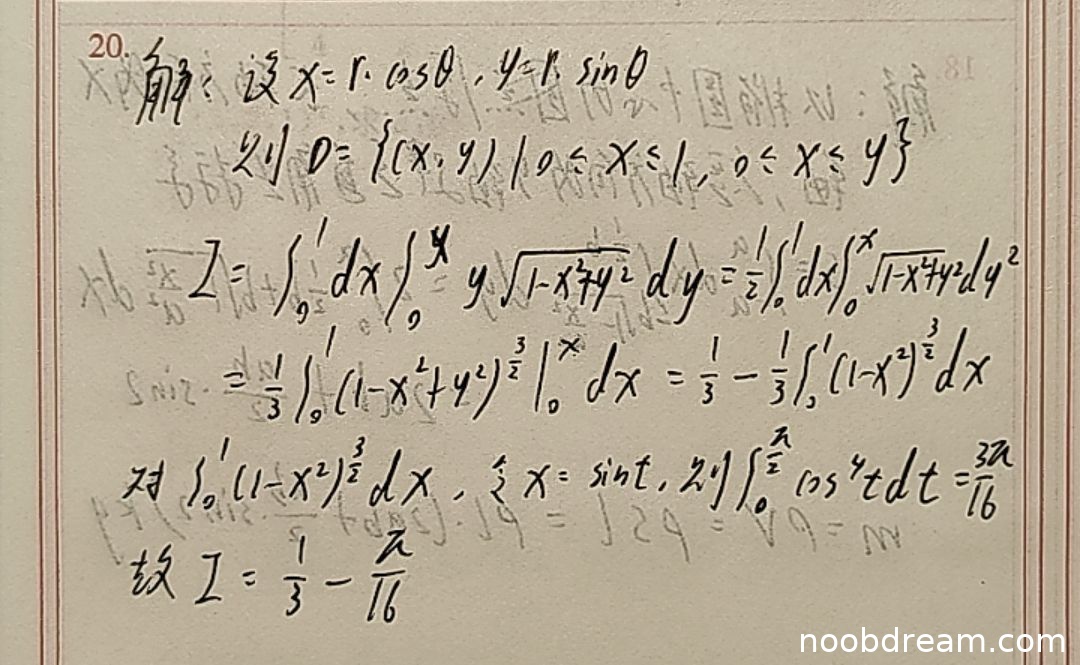
评分及理由
(1)得分及理由(满分10分)
学生作答存在以下问题:
- 积分区域描述错误:学生写为 \(D=\{(x,y)|0\leq x\leq1,0\leq x\leq y\}\),正确应为 \(0 \leq x \leq 1, 0 \leq y \leq x\)。这是明显的逻辑错误,扣2分。
- 第一次识别中积分表达式有误:\(\int_{0}^{y}y\sqrt{1 - x^{2}+y^{2}}dy\) 应为 \(\int_{0}^{x}y\sqrt{1 - x^{2}+y^{2}}dy\),扣1分。
- 第二次识别中换元步骤有误:\(\int_{0}^{x^{2}}\sqrt{1 - x^{2}+u}du\) 的积分限应为从 \(1-x^2\) 到 \(1\),扣1分。
- 计算过程中有书写错误但最终结果正确:如第一次识别中的 \(1 - x^{4}+y^{2}\) 应为 \(1 - x^{2}+y^{2}\),但后续计算修正了,不扣分。
最终结果正确,思路基本正确,但存在上述逻辑错误。扣除4分,得6分。
题目总分:6分

评分及理由
(1)得分及理由(满分10分)
第1次识别结果:
- 正确构造辅助函数 F(x) = f(x) - 1/3 x³,得2分
- 正确应用拉格朗日中值定理于[0,1/2]区间,得2分
- 正确应用拉格朗日中值定理于[1/2,1]区间,得2分
- 两式相加时出现逻辑错误:F'(ξ)+F'(η) = 2(F(1)-F(0)) = 0 这一步推导错误,因为F(1/2)项未正确处理,扣2分
- 最终结论正确,得2分
- 小计:2+2+2-2+2 = 6分
第2次识别结果:
- 正确构造辅助函数,得2分
- 正确应用拉格朗日中值定理于[0,1/2]区间,得2分
- 正确应用拉格朗日中值定理于[1/2,1]区间,得2分
- 两式相加时出现逻辑错误:F'(ξ)+F'(η) = 2(F(1)-F(0)) = 0 这一步推导错误,扣2分
- 最终结论正确,得2分
- 小计:2+2+2-2+2 = 6分
根据评分要求第3条,两次识别中取较高分,本题得分为6分。
题目总分:6分

评分及理由
(1)得分及理由(满分6分)
第一次识别:学生正确写出r(A)=r(A,b)<3,并计算|A|=0得到λ=1或-1。在λ=1时正确判断r(A)≠r(A,b)。在λ=-1时进行初等行变换,但变换过程有误(第三行应为[1,1,-1,1]但学生写为[-1,-1,1]),不过最终得到a=-2的结论正确。由于核心思路正确且得到正确答案,但变换过程有误,扣1分,得5分。
第二次识别:存在明显错误,将λ误写为a,导致逻辑混乱。但后续计算仍按λ=-1进行,得到a=-2正确。由于变量符号错误导致逻辑不严谨,扣2分,得4分。
按两次识别中较高分计,得5分。
(2)得分及理由(满分6分)
第一次识别:学生正确写出增广矩阵行简化形式,齐次方程通解正确,但特解计算错误(应为(3/2,-1/2,0)ᵀ而非(5/2,-1/2,1)ᵀ)。由于特解错误,扣2分,得4分。
第二次识别:增广矩阵行简化形式正确,齐次方程通解正确,但特解计算错误(应为(3/2,-1/2,0)ᵀ而非(-5/2,-1/2,1)ᵀ)。由于特解错误,扣2分,得4分。
按两次识别中较高分计,得4分。
题目总分:5+4=9分

评分及理由
(1)a的求解得分及理由(满分2分)
学生正确利用特征向量定义 \(A\alpha_1 = \lambda_1\alpha_1\) 求解a值。第一次识别中计算过程有误(向量分量写错),但第二次识别中计算正确得到a=-1。根据禁止扣分规则第3条,只要有一次识别正确就不扣分。得2分。
(2)特征值求解得分及理由(满分2分)
学生正确计算特征多项式并得到特征值λ₁=2, λ₂=-4, λ₃=5。两次识别结果一致且正确。得2分。
(3)特征向量求解得分及理由(满分3分)
第一次识别:λ₂=-4对应的特征向量正确为(-1,0,1)ᵀ,但λ₃=5对应的特征向量计算有误。
第二次识别:λ₂=-4对应的特征向量错误为(0,1,0)ᵀ,λ₃=5对应的特征向量正确为(1,-1,1)ᵀ。
根据禁止扣分规则第3条,只要有一次识别正确就不扣分,但这里两个特征向量在不同识别中各有一个正确,综合考虑,特征向量求解部分存在明显错误,扣1分。得2分。
(4)正交化单位化得分及理由(满分2分)
第一次识别:对β₂,β₃进行了正交化处理,但计算错误。
第二次识别:直接对错误的特征向量进行单位化,没有进行必要的正交化。
由于特征向量本身有误,且正交化处理不当,扣1分。得1分。
(5)正交矩阵Q构造得分及理由(满分2分)
学生最终给出的Q矩阵与标准答案不一致,且由于前面特征向量求解错误,导致Q矩阵构造错误。扣2分。得0分。
题目总分:2+2+2+1+0=7分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


