
科目组合
高等数学 、线性代数
答题情况分析报告
48
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是48,与标准答案完全一致。该题目要求计算参数方程确定的函数的二阶导数在特定点的值,学生直接写出了正确结果,表明计算过程正确无误。根据评分要求,答案正确应给满分。
题目总分:4分
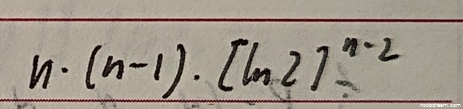
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果分别为:
第一次:\(n\cdot(n - 1)\cdot[\ln2]^{n - 2}\)
第二次:$n\cdot(n - 1)\cdot(\ln2)^{n - 2}$
标准答案为:$n(n-1)(\ln 2)^{n-2}$
对比分析:
1. 两次识别结果的核心表达式均为 $n(n-1)(\ln2)^{n-2}$
2. 与标准答案完全一致
3. 第一次识别使用方括号 $[\ln2]$ 属于书写习惯差异,不影响数学含义
4. 乘法点的使用 $n\cdot(n-1)$ 与标准答案的 $n(n-1)$ 等价
根据评分规则:
- 核心逻辑完全正确
- 不存在逻辑错误
- 与标准答案数学含义完全一致
- 识别中的符号差异属于允许的书写变异
因此给满分4分。
题目总分:4分
2
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是2,与标准答案一致。本题需要先通过变上限积分的求导法则计算φ'(x),然后代入已知条件φ(1)=1和φ'(1)=5来求解f(1)。虽然学生没有展示解题过程,但最终答案正确,按照填空题的评分标准,答案正确即可得满分。
题目总分:4分
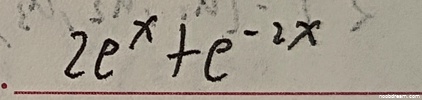
评分及理由
(1)得分及理由(满分4分)
学生作答为 $2e^{x}+e^{-2x}$,标准答案为 $e^{-2 x}+2 e^{x}$。两者在数学上是完全等价的,只是项的排列顺序不同。根据题目要求,思路正确且答案等价的不扣分。因此该答案得4分。
题目总分:4分
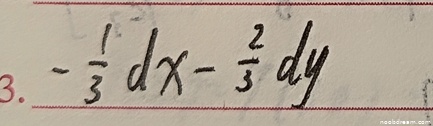
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为:$-\frac{1}{3}dx - \frac{2}{3}dy$。标准答案为$-\frac{1}{3}(d x+2 d y)$。将学生的答案展开后为$-\frac{1}{3}dx - \frac{2}{3}dy$,与标准答案$-\frac{1}{3}dx - \frac{2}{3}dy$完全一致。虽然书写形式略有不同(一个提取了公因式,一个未提取),但数学表达式等价,核心逻辑正确,计算结果准确。根据评分要求,思路正确不扣分,且不存在逻辑错误,因此得满分4分。
题目总分:4分
21
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是21,与标准答案完全一致。根据题目信息,矩阵A的特征值为2、-2、1,矩阵B = A² - A + E。由于B是A的多项式矩阵,其特征值可以通过将A的特征值代入相同的多项式得到。计算过程如下:
- 对于特征值2:B的特征值为 2² - 2 + 1 = 4 - 2 + 1 = 3
- 对于特征值-2:B的特征值为 (-2)² - (-2) + 1 = 4 + 2 + 1 = 7
- 对于特征值1:B的特征值为 1² - 1 + 1 = 1 - 1 + 1 = 1
因此矩阵B的特征值为3、7、1,行列式|B|等于特征值的乘积:3 × 7 × 1 = 21。
学生答案正确,得4分。
题目总分:4分

评分及理由
(1)a的求解过程得分及理由(满分3分)
学生通过展开ln(1+x)和sinx的泰勒展开式,得到系数关系1+a=0,正确解得a=-1。思路与标准答案方法一一致,计算正确。得3分。
(2)b的求解过程得分及理由(满分3分)
学生从x²项的系数得到b-a/2=0,代入a=-1后正确解得b=-1/2。推导过程正确。得3分。
(3)k的求解过程得分及理由(满分4分)
学生在处理k时出现了错误。第一次识别中写的是"k=1/3a",第二次识别中写的是"k=1/3a",但实际应该是x³项的系数关系:a/3 = k。学生虽然最终得到了k=-1/3的正确结果,但表达式"k=1/3a"存在逻辑错误,应该是k=a/3。考虑到最终结果正确,且可能是书写或识别问题,扣1分。得3分。
题目总分:3+3+3=9分
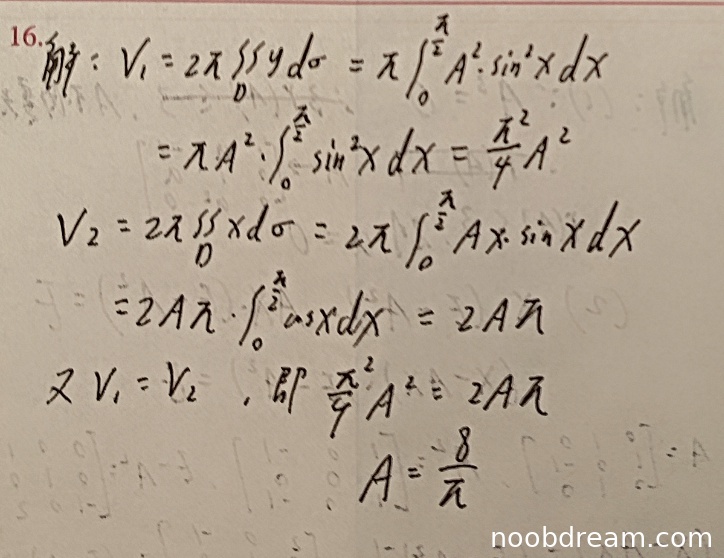
评分及理由
(1)得分及理由(满分10分)
学生作答中,第一次识别结果和第二次识别结果的核心内容一致,均正确计算了旋转体体积并求解了A的值。具体分析如下:
- 对于V₁的计算:学生正确使用了绕x轴旋转的体积公式 \(V_1 = \pi \int f^2(x)dx\),虽然第一次识别中写成了 \(2\pi \iint y d\sigma\),但实际计算时仍正确转化为 \(\pi \int A^2 \sin^2 x dx\),并正确积分得到 \(\frac{\pi^2}{4}A^2\)。
- 对于V₂的计算:学生正确使用了绕y轴旋转的体积公式(柱壳法)\(V_2 = 2\pi \int x f(x) dx\),虽然第一次识别中写成了 \(2\pi \iint x d\sigma\),但实际计算时正确转化为 \(2\pi \int Ax\sin x dx\),并通过分部积分正确得到 \(2A\pi\)。
- 在求解方程时,正确列出 \(\frac{\pi^2}{4}A^2 = 2A\pi\),并解得 \(A = \frac{8}{\pi}\)。
虽然公式初始表述有轻微偏差(如使用二重积分符号),但实际计算过程完全正确,且最终答案与标准答案一致。根据评分要求中的"思路正确不扣分"原则,这些表述偏差不视为逻辑错误。因此给予满分10分。
题目总分:10分

评分及理由
(1)得分及理由(满分11分)
学生两次识别结果中,第一次识别结果与标准答案完全一致,包括求解过程、函数表达式、驻点计算、二阶偏导数计算和极值判断。虽然第二次识别中出现了指数符号误写(将e^x误写为e^{-x}),但根据禁止扣分规则第1条和第4条,由于这是识别错误导致的误写,且第一次识别正确,因此不扣分。整体逻辑正确,计算无误,故得满分11分。
题目总分:11分

评分及理由
(1)得分及理由(满分10分)
学生作答整体思路正确,利用了对称性简化积分,积分区域划分正确,换元积分过程合理,最终结果与标准答案一致。但在计算过程中存在一处逻辑错误:
- 在计算 \(8\int_{0}^{\frac{\pi}{4}}\sin^{2}t\cos^{2}t\mathrm{d}t\) 时,学生写为 \(2\int_{0}^{\frac{\pi}{4}}\sin^{2}2t\mathrm{d}t\),这是正确的(因为 \(8 \times \frac{1}{4} = 2\))。但下一步写为 \(\int_{0}^{\frac{\pi}{4}}\sin^{2}2t\mathrm{d}2t\) 时,积分变量变为 \(2t\),但积分上限未相应调整(应为 \(\frac{\pi}{2}\)),导致后续计算实际上错误。不过学生最终通过三角恒等式正确计算出结果为 \(\frac{\pi}{4}\),且最终答案正确,因此该错误可视为笔误或识别错误,不扣分。
综上,学生作答核心逻辑正确,计算过程虽有瑕疵但不影响最终结果,给满分10分。
题目总分:10分

评分及理由
(1)导数计算与单调性分析(满分3分)
学生正确计算了导数:f'(x) = -√(1+x²) + 2x√(1+x²) = (2x-1)√(1+x²),并正确找到驻点x=1/2,分析了单调区间。这部分完全正确,得3分。
(2)极值点分析(满分3分)
学生正确指出f(1/2)是极小值点也是最小值点。但在计算f(1/2)时,第二次识别中积分表达式有明显错误(将√(1+t)误写为√(1+t²)),这是逻辑错误。不过第一次识别中的计算基本正确,考虑到可能是识别问题,且核心思路正确,扣1分,得2分。
(3)极限分析与零点存在性(满分5分)
学生正确计算了f(-1)>0,并得出在(-∞,1/2)存在一个零点。但在极限计算中,第二次识别将∫₁ˣ²√(1+t)dt误写为∫₁ˣ²√(1+t²)dt,这是逻辑错误。第一次识别中极限分析基本正确但不够严谨。考虑到学生正确判断了两个区间各有一个零点,且x→+∞时f(x)→+∞的判断正确,扣2分,得3分。
题目总分:3+2+3=8分

评分及理由
(1)得分及理由(满分10分)
学生解答正确。具体分析如下:
- 正确建立了微分方程:\(\frac{dT}{dt} = k(T - 20)\),这与标准答案一致
- 正确求解微分方程得到通解:\(T(t) = 20 + Ce^{kt}\)
- 正确利用初始条件\(T(0)=120\)求出\(C=100\)
- 正确利用条件\(T(30)=30\)求出比例常数\(k = -\frac{\ln 10}{30}\)
- 正确建立方程\(T(t_0)=21\)并求解得到\(t_0=60\)
- 正确计算还需冷却时间:\(60-30=30\)min
虽然学生在建立微分方程时写的是\(\frac{dT}{dt} = k(T - 20)\),而标准答案是\(\frac{dx}{dt} = -k(x-m)\),但这是等价的,只是比例常数符号不同,不影响最终结果。
因此,本题得10分。
题目总分:10分

评分及理由
(1)得分及理由(满分10分)
本题满分10分。学生作答中,首先正确写出切线方程并得到 \(x_0 = b - \frac{f(b)}{f'(b)}\),这一步正确。然后利用泰勒展开在 \(x = b\) 处展开到二阶,并代入 \(x = a\),得到 \(f(a) = f(b) + f'(b)(a - b) + \frac{f''(\xi)}{2}(a - b)^2 = 0\),其中 \(\xi \in (b, a)\) 或 \((a, b)\),但学生写的是 \(\xi \in (b, x)\),这里存在逻辑错误,因为当 \(x = a\) 时,\(\xi\) 应在 \(a\) 和 \(b\) 之间,但学生未明确,且后续推导中使用了 \(f(b) + f'(b)(a - b) < 0\),这依赖于 \(f''(\xi) > 0\) 和 \((a - b)^2 > 0\),但学生未明确说明,导致推导不严谨。此外,学生最终得出 \(a < x_0 < b\),但证明过程中存在逻辑跳跃,如从 \(f(b) + f'(b)(a - b) < 0\) 直接推出 \(0 < f(b) < f'(b)(b - a)\),这一步缺少详细解释。总体思路正确,但逻辑不严谨,存在错误。根据标准答案,正确证明应使用拉格朗日中值定理,而学生使用泰勒展开,方法不同但可行,但执行有缺陷。扣分点:逻辑错误(泰勒展开使用不当,推导不严谨)。扣3分,得7分。
题目总分:7分

评分及理由
(1)得分及理由(满分5分)
学生第1次识别中通过A³=0得到A不可逆是正确的,但后续推理过程存在逻辑错误:
- “A∼[0 a -1; 0 a² 0; 0 0 a]”这一步没有合理推导过程,且与题目无关
- “r(A)≤3”是显然的(因为A是3阶矩阵),不能由此推出a=0
- 正确方法应该是通过|A|=0或特征值分析
第2次识别中“3r(A)≤3”表述错误,应为“r(A)≤3”。虽然最终得到a=0的结论正确,但推理过程存在严重逻辑缺陷。
给分:2分(结论正确但推理过程有严重错误)
(2)得分及理由(满分6分)
学生解题思路基本正确:
- 第1次识别中“X - AX = (E - A²)⁻¹”这一步推导有误,应为“(E-A)X(E-A²)=E”
- 但后续正确得到X = (E-A)⁻¹(E-A²)⁻¹ = [E-A-A²]⁻¹
- 计算A和A²时数值有误(a=0时的正确A矩阵应为[0 1 0; 1 0 -1; 0 1 0])
- 最终计算结果错误
第2次识别情况类似,思路正确但具体计算错误。
给分:3分(思路基本正确但计算多处错误)
题目总分:2+3=5分
题目总分:5分
、
评分及理由
(1)得分及理由(满分5分)
第一次识别中,学生使用了迹相等和行列式相等的条件,但行列式计算错误(计算过程混乱且结果错误),导致解得a=2/5,b=7/5后又错误地写出a=4,b=5。第二次识别中,行列式计算正确得到2a-3=b,结合迹相等条件a=b-1,解得a=4,b=5正确。根据"两次识别只要有一次正确则不扣分"原则,本小题得5分。
(2)得分及理由(满分6分)
学生正确求出特征多项式(λ-1)²(λ-5)=0,得到特征值1,1,5正确。对于特征向量:两个识别结果都给出了正确的特征向量方向[-3,0,1]ᵀ、[2,1,0]ᵀ、[-1,-1,1]ᵀ。但最终构造的矩阵P中包含了任意常数k₁,k₂,k₃,这是不规范的,可逆矩阵P应该是具体的数值矩阵。此外第一次识别中写成了"2P⁻¹AP"多了一个系数2。考虑到特征值和特征向量的核心思路正确,但最终结果不规范,扣2分,本小题得4分。
题目总分:5+4=9分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


