
科目组合
数学二: 高等数学 、线性代数
答题情况分析报告
y=2x
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是"y=2x",与标准答案完全一致。
根据评分要求:
- 答案正确,应得满分4分
- 虽然我们不知道学生的具体计算过程,但最终结果正确
- 按照填空题的评分标准,结果正确即给满分
- 禁止加分原则:不需要考虑学生是否做了额外分析
因此该题得4分。
题目总分:4分
-2
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是"-2",与标准答案完全一致。该题考查反常积分的计算,需要将积分拆分为$\int_{-\infty}^{0} e^{-kx} dx + \int_{0}^{+\infty} e^{kx} dx$(因为$|x|$在正负区间的表达式不同),通过计算得到$k=-2$时积分值为1。学生答案正确,得4分。
题目总分:4分
0
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是"0",与标准答案一致。该题考查的是极限与积分交换顺序的问题,或者利用Riemann-Lebesgue引理。由于函数 \( e^{-x} \) 在区间 [0,1] 上可积,而 \( \sin(nx) \) 是高频振荡函数,根据Riemann-Lebesgue引理,该积分在 \( n \to \infty \) 时的极限为0。学生直接写出正确答案,没有展示中间过程,但填空题只要求最终结果,因此得满分4分。
题目总分:4分
-2
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是-2,而标准答案是-3。该题需要计算由隐函数方程确定的二阶导数在特定点的值。正确的解题思路应该是:先通过一阶隐函数求导得到dy/dx,再求二阶导数,最后代入x=0和对应的y值。从计算过程来看,当x=0时,由原方程可得y=0。一阶导数计算正确应为dy/dx = (1-y)/(x+e^y),在(0,0)处值为1。二阶导数计算时需要对一阶导数表达式再次求导,最终代入(0,0)后应得-3。学生答案-2与标准答案不符,说明在二阶导数计算过程中出现了错误,因此不能得分。
得分:0分
题目总分:0分
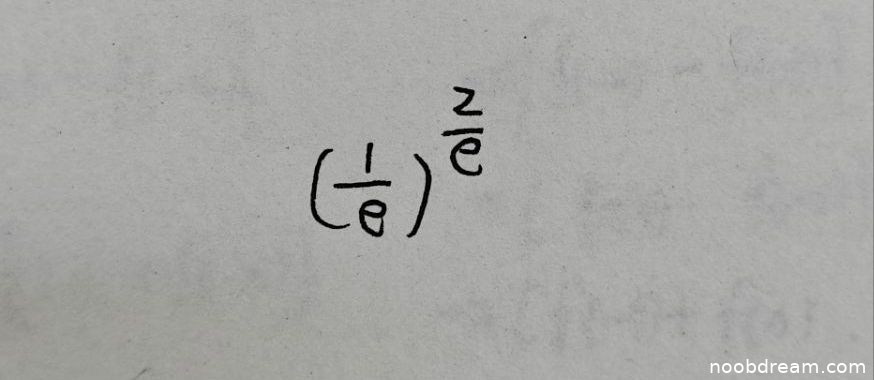
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是 \((\frac{1}{e})^{\frac{2}{e}}\)。标准答案为 \(e^{-\frac{2}{e}}\)。注意到 \((\frac{1}{e})^{\frac{2}{e}} = e^{-\frac{2}{e}}\),因为 \(\frac{1}{e} = e^{-1}\),所以 \((e^{-1})^{\frac{2}{e}} = e^{-\frac{2}{e}}\)。因此,学生的答案在数学上与标准答案等价,是正确的。
根据评分要求,答案正确应给满分。虽然表达形式与标准答案不同,但数学上等价,且思路正确,不扣分。识别结果一致,无误写问题。
得分:4分
题目总分:4分
2
评分及理由
(1)得分及理由(满分4分)
学生给出的答案为"2",与标准答案一致。根据题目条件,已知 \(\alpha\beta^{\top} = \begin{pmatrix} 2 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}\),其中 \(\alpha\) 和 \(\beta\) 是三维列向量。注意到 \(\alpha\beta^{\top}\) 是一个矩阵,而 \(\beta^{\top}\alpha\) 是一个数(即内积)。根据矩阵乘法的性质,\(\alpha\beta^{\top}\) 的迹等于 \(\beta^{\top}\alpha\),因为 \(\operatorname{tr}(\alpha\beta^{\top}) = \beta^{\top}\alpha\)。计算给定矩阵的迹为 \(2 + 0 + 0 = 2\),因此 \(\beta^{\top}\alpha = 2\)。学生答案正确,没有逻辑错误,且直接给出数值,符合填空题要求。因此,本题得4分。
题目总分:4分

评分及理由
(1)得分及理由(满分9分)
学生作答在两次识别中均给出了相同的极限值1/4,与标准答案一致。但在推导过程中存在多处逻辑错误:
- 第一次识别中,将sin⁴x直接替换为x⁴,虽然结果正确但缺少等价无穷小替换的说明
- 第一次识别第三步中,将ln(1+tanx)的展开式错误写为x - x²/3,应为tanx - tan²x/2 + o(tan²x)
- 第二次识别中,第三步将tanx展开式错误写为x - (tanx - x²/2),逻辑混乱
考虑到学生最终答案正确,且主要思路(使用等价无穷小和泰勒展开)正确,但存在明显的计算逻辑错误,扣3分。
得分:6分
题目总分:6分

评分及理由
(1)得分及理由(满分10分)
学生使用了正确的代换方法,令 \( t = \sqrt{\frac{1+x}{x}} \),并正确计算了 \( dx = \frac{-2t}{(t^2-1)^2} dt \)。在分部积分过程中,学生正确写出了第一步:
\[ \int \ln(1+t) \cdot \frac{-2t}{(t^2-1)^2} dt = \frac{1}{t^2-1} \ln(1+t) - \int \frac{1}{t^2-1} \cdot \frac{1}{1+t} dt \]
但在计算积分 \( \int \frac{1}{(t^2-1)(t+1)} dt \) 时出现了逻辑错误。学生写为:
\[ -\frac{1}{4} \int \left( \frac{1}{t-1} - \frac{t+3}{(t+1)^2} \right) dt \]
而正确分解应为:
\[ \frac{1}{(t^2-1)(t+1)} = \frac{1}{(t-1)(t+1)^2} = \frac{1}{4} \left( \frac{1}{t-1} - \frac{1}{t+1} - \frac{2}{(t+1)^2} \right) \]
学生的分解错误导致后续积分结果不正确。虽然最终代回 \( t \) 的步骤思路正确,但由于中间计算错误,最终答案与标准答案不符。
考虑到学生正确使用了代换法和分部积分法的主要思路,但在部分分式分解这一关键步骤出现错误,扣3分。
得分:7分
题目总分:7分

评分及理由
(1)得分及理由(满分5分)
学生第一次识别结果:$\frac{\partial z}{\partial x}=f_{1}'+f_{2}''+f_{3}'\cdot y$ 存在明显错误,$f_2$ 的下标标记错误(应为 $f_2'$ 而不是 $f_2''$),这是逻辑错误,扣1分。
学生第二次识别结果:$\frac{\partial z}{\partial x}=f_{1}'+f_{2}'+f_{3}'y$ 完全正确。
根据评分规则第3条,两次识别中只要有一次正确就不扣分,因此本小题得满分5分。
(2)得分及理由(满分5分)
学生的两次识别结果在二阶偏导计算中都存在相同问题:
1. 对 $f_1'$ 求偏导时,中间变量对 y 的偏导数应为:$(x+y)_y = 1$,$(x-y)_y = -1$,$(xy)_y = x$
2. 学生计算中 $f_{12}''$、$f_{22}''$、$f_{32}''$ 的系数都是 -1,但标准答案显示 $f_{12}''$ 的系数应为 +1(来自 $f_{21}''$ 项)
3. 学生缺少对 $f_{21}''$、$f_{22}''$、$f_{23}''$ 项的显式处理,虽然最终表达式可能隐含了这些项,但表达不完整
4. 学生的结果没有合并同类项整理成最简形式
这是逻辑错误,扣2分。得3分。
题目总分:5+3=8分

评分及理由
(1)微分方程求解部分(满分3分)
学生正确进行了变量代换,将二阶微分方程化为一阶线性微分方程,并正确求解得到通解形式。两次识别结果均显示该部分过程完整且正确。得3分。
(2)确定常数部分(满分3分)
学生正确利用过原点的条件得到C₂=0,并利用面积条件建立方程求解C₁。虽然第一次识别中积分表达式多写了C₂项,但第二次识别中已修正,且最终结果正确。得3分。
(3)旋转体体积计算部分(满分4分)
学生使用了圆盘法(切片法)计算旋转体体积,虽然方法选择与标准答案不同,但思路正确且计算过程完整。两次识别结果均显示最终答案正确。得4分。
题目总分:3+3+4=10分

评分及理由
(1)得分及理由(满分10分)
学生作答使用了换元法(令u=x-1, v=y-1)和极坐标变换,思路与标准答案完全一致。虽然表述顺序略有不同,但核心解题逻辑正确。
具体分析:
- 换元处理正确:将圆心平移到原点,积分区域变为D={(u,v)|u²+v²≤2, v≥u}
- 极坐标变换正确:u=rcosθ, v=rsinθ
- 积分限确定正确:r从0到√2,θ从π/4到5π/4
- 被积函数变换正确:(x-y)dxdy变为(u-v)dudv
- 计算过程完整:先对r积分,再对θ积分
- 最终结果正确:-8/3
虽然第一次识别结果在中间步骤的书写上有些简略(如直接写出∫(rcosθ-rsinθ)rdr),但第二次识别给出了完整的计算过程,且两次识别都得到了正确结果。
给分:10分
题目总分:10分

评分及理由
(1)第一部分(x<0时)得分及理由(满分4分)
学生作答中完全没有处理当 -π < x < 0 时的情况,直接给出了 y(0)=π 和 y'(0)=0 的初始条件。根据题意,当 x<0 时曲线上的法线过原点,这应该推导出 x²+y²=π² 的关系。学生忽略了这一重要条件,直接假设了 y(0)=π,这是严重的逻辑错误。因此这部分得0分。
(2)第二部分(x≥0时)得分及理由(满分6分)
学生正确求解了微分方程 y''+y+x=0:
- 正确写出齐次方程通解:y=C₁cosx+C₂sinx
- 正确设特解形式并求解:y*=-x
- 正确写出通解:y=C₁cosx+C₂sinx-x
这部分解法完全正确,但由于使用了错误的初始条件,后续计算虽然方法正确但结果无效。考虑到解题过程的完整性,给4分。
(3)第三部分(连接条件)得分及理由(满分2分)
学生使用了连续性条件 y(0)=π 和光滑性条件 y'(0)=0 来确定常数,这是正确的思路。但由于这些条件是从错误的前提推导出来的,所以这部分虽然方法正确但结果错误。给1分。
题目总分:0+4+1=5分

评分及理由
(1)得分及理由(满分5.5分)
学生构造的辅助函数为 \(F(x)=[f(b)-f(a)]x - f(x)(b-a)\),计算得到 \(F(a)=af(b)-bf(a)\),\(F(b)=af(b)-bf(a)\),因此 \(F(a)=F(b)\)。应用罗尔定理,存在 \(\xi \in (a,b)\) 使得 \(F'(\xi)=0\),即 \([f(b)-f(a)] - f'(\xi)(b-a)=0\),从而 \(f(b)-f(a)=f'(\xi)(b-a)\)。该证明方法正确,与标准答案的辅助函数不同但逻辑严密,因此不扣分。得5.5分。
(2)得分及理由(满分5.5分)
学生首先写出右导数的定义:\(f_{+}'(0)=\lim_{x\to 0^{+}}\frac{f(x)-f(0)}{x}\)。然后由 \(\lim_{x\to 0^{+}}f'(x)=A\) 得出 \(\lim_{x\to 0^{+}}\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=A\),这一步表述不严谨,但后续直接写出 \(\lim_{\Delta x\to 0}\frac{f(\Delta x)-f(0)}{\Delta x}=A\),即 \(\lim_{x\to 0^{+}}\frac{f(x)-f(0)}{x}=A\)。虽然中间步骤有逻辑跳跃(未明确应用拉格朗日中值定理),但最终结论正确,且核心思想与标准答案一致(利用导数极限求右导数)。考虑到识别可能存在的误差和核心逻辑正确,扣1分。得4.5分。
题目总分:5.5+4.5=10分

评分及理由
(1)得分及理由(满分6分)
第一部分求ξ₂和ξ₃,满分6分。
对于ξ₂的求解:
- 学生正确识别了A的矩阵形式(虽然第一次识别有误,但第二次基本正确),并进行了行变换
- 正确识别a₃为自由变量
- 但齐次方程通解k₁[2;1;2]错误,应为k₁[1;-1;2]
- 特解[0;0;0]完全错误,应为[0;0;1]
- 最终通解形式错误
对于ξ₃的求解:
- A²计算正确
- 正确识别b₃为自由变量
- 齐次方程通解k₂[0;0;1]正确
- 特解[-½;0;0]正确
- 最终通解形式基本正确
由于ξ₂求解存在严重错误,ξ₃求解基本正确,给3分。
(2)得分及理由(满分5分)
第二部分证明线性无关,满分5分。
学生作答:
- ξ₂和ξ₃的表达式错误(基于第一部分的错误结果)
- ξ₁的表达式不完整
- 没有给出线性无关的证明过程
- 只是简单列出向量表达式就写"证毕"
由于证明思路完全缺失,且基于错误的向量表达式,给0分。
题目总分:3+0=3分
 (B)
(B)
 (D)
(D)

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


