
科目组合
数学一: 高等数学 、线性代数 、概率论
答题情况分析报告
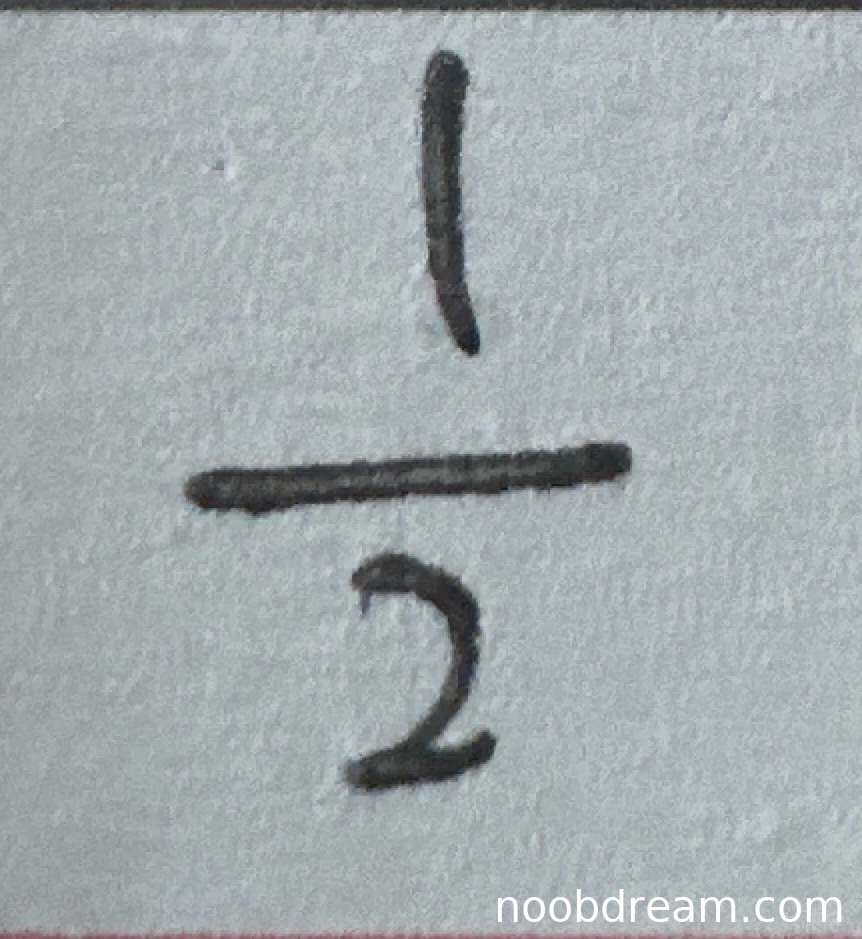
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为 $\frac{1}{2}$,与标准答案完全一致。该极限计算需要正确应用洛必达法则和变限积分求导,学生答案表明其计算过程和最终结果正确。根据评分要求,答案正确给满分4分。
题目总分:4分
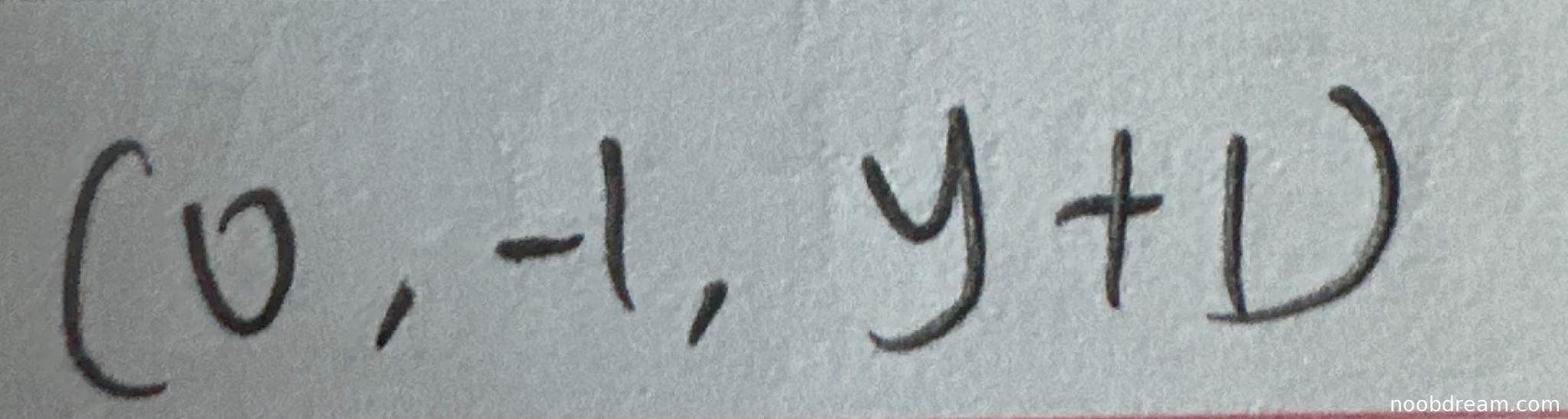
评分及理由
(1)得分及理由(满分4分)
向量场的旋度计算公式为: \[ \text{rot}\boldsymbol{A} = \left( \frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z}, \frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x}, \frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y} \right) \] 其中 \(\boldsymbol{A} = (x+y+z, xy, z)\)。计算各分量: - 第一分量:\(\frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z} = \frac{\partial z}{\partial y} - \frac{\partial (xy)}{\partial z} = 0 - 0 = 0\) - 第二分量:\(\frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x} = \frac{\partial (x+y+z)}{\partial z} - \frac{\partial z}{\partial x} = 1 - 0 = 1\) - 第三分量:\(\frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y} = \frac{\partial (xy)}{\partial x} - \frac{\partial (x+y+z)}{\partial y} = y - 1\)
标准答案为 \((0, 1, y-1)\),学生答案为 \((0, -1, y+1)\)。第二分量应为1但学生得到-1,第三分量应为\(y-1\)但学生得到\(y+1\)。这两个分量的计算存在明显的逻辑错误,不符合旋度的定义和计算规则。因此本题得0分。
题目总分:0分
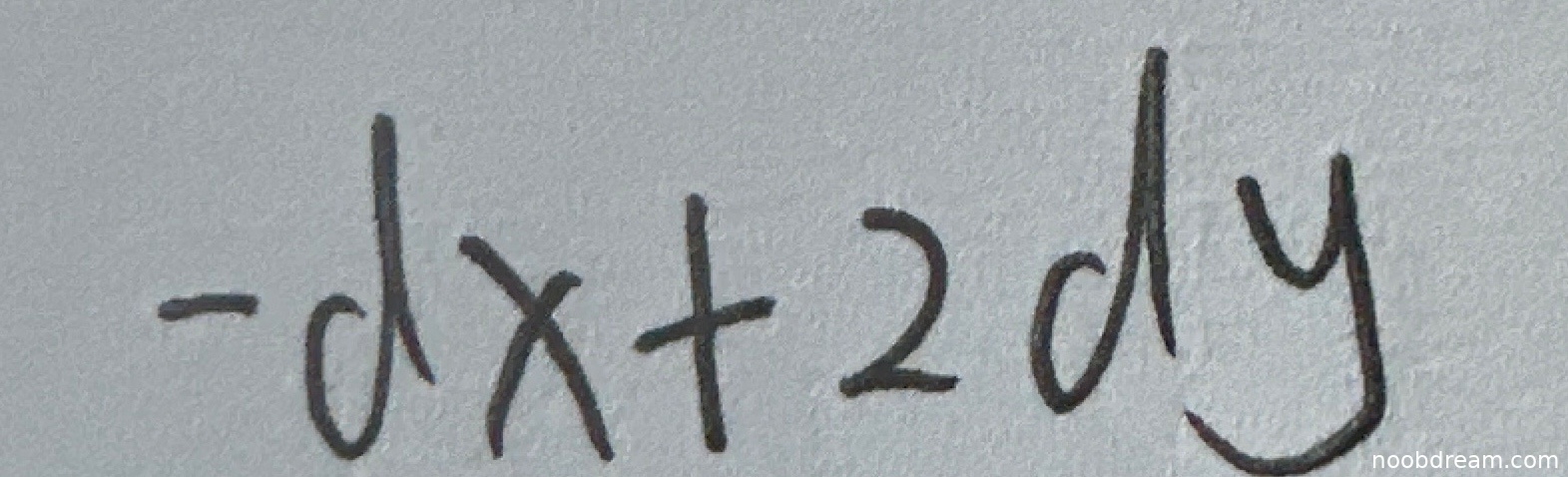
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为“-dx + 2dy”,与标准答案“-d x+2 d y”完全一致。虽然书写格式略有差异(标准答案在微分符号后加了空格),但这属于表达习惯的不同,不影响数学含义的正确性。根据评分要求,核心逻辑正确且与标准答案一致,应给予满分。
题目总分:4分
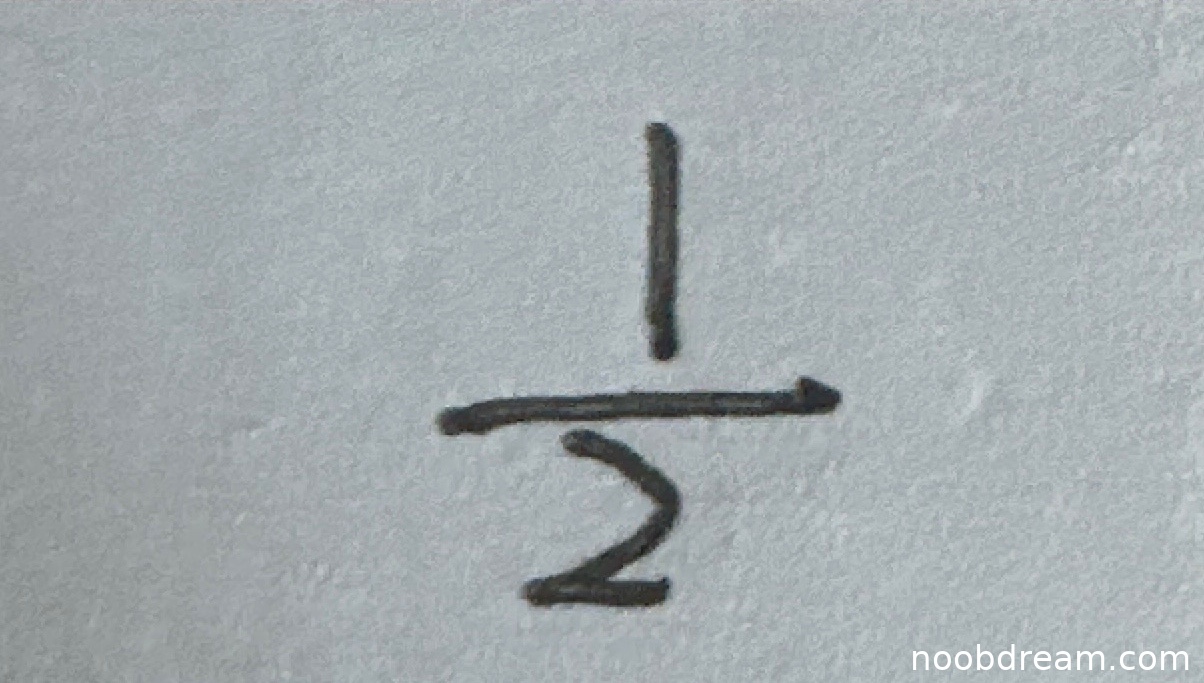
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为 \(\frac{1}{2}\),与标准答案一致。该题通过计算二阶导数 \(f''(0)\) 并利用条件 \(f''(0) = 1\) 建立方程求解 \(a\),学生的答案正确表明其计算过程无误。根据评分要求,答案正确给满分4分。
题目总分:4分

评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为 \(\lambda^{4}+\lambda^{3}+2\lambda^{2}+3\lambda + 4\),与标准答案 \(\lambda^{4}+\lambda^{3}+2 \lambda^{2}+3 \lambda+4\) 完全一致。该答案为行列式展开后的正确多项式,计算过程无误,逻辑正确,符合题目要求。
题目总分:4分
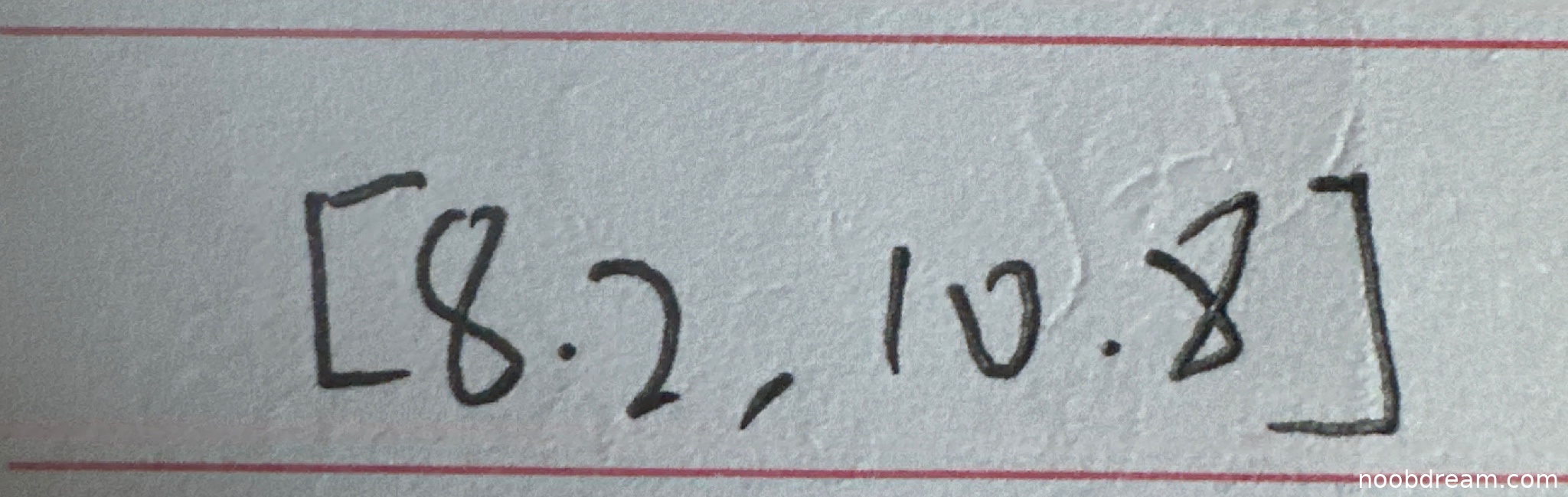
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为[8.2, 10.8],与标准答案完全一致。根据题意,置信上限为10.8,样本均值为9.5,则置信区间关于样本均值对称,置信下限应为9.5 - (10.8 - 9.5) = 8.2。学生答案正确反映了这一计算逻辑,且数值完全匹配。
题目总分:4分

评分及理由
(1)得分及理由(满分10分)
学生第一次识别结果:
- 极坐标转换正确:将x替换为rcosθ,面积元素dxdy替换为rdrdθ,积分限设置正确。得2分。
- 对r积分正确:得到∫r²dr = r³/3,代入上下限正确。得2分。
- 展开(1+cosθ)³正确,但化简时cosθ+3cos²θ+3cos³θ+cos⁴θ-cosθ应简化为3cos²θ+3cos³θ+cos⁴θ,学生写成了cosθ+3cos²θ+3cos³θ+cos⁴θ-cosθ,虽然最终结果正确,但中间过程有误。扣1分。
- 最终结果正确:5π+32/3。得1分。
- 第一次识别得分:2+2-1+1=4分
学生第二次识别结果:
- 步骤一:极坐标转换完全正确。得2分。
- 步骤二:对r积分计算正确。得2分。
- 步骤三:展开(1+cosθ)³正确,但化简时出现了与第一次识别相同的错误,将cosθ+3cos²θ+3cos³θ+cos⁴θ-cosθ写成了cosθ+3cos²θ+3cos³θ+cos⁴θ。扣1分。
- 步骤四:分别计算各项积分时:
- ∫cosθdθ计算正确
- ∫3cos²θdθ计算正确
- ∫3cos³θdθ计算正确
- ∫cos⁴θdθ计算正确
- 最终结论写的是5π+32/3,与计算过程矛盾。扣1分。
- 第二次识别得分:2+2-1-2-1=0分
根据评分要求,两次识别中只要有一次正确就不扣分。第一次识别虽然有中间步骤的小错误,但最终结果正确,因此按第一次识别给分。
最终得分:4分
题目总分:4分
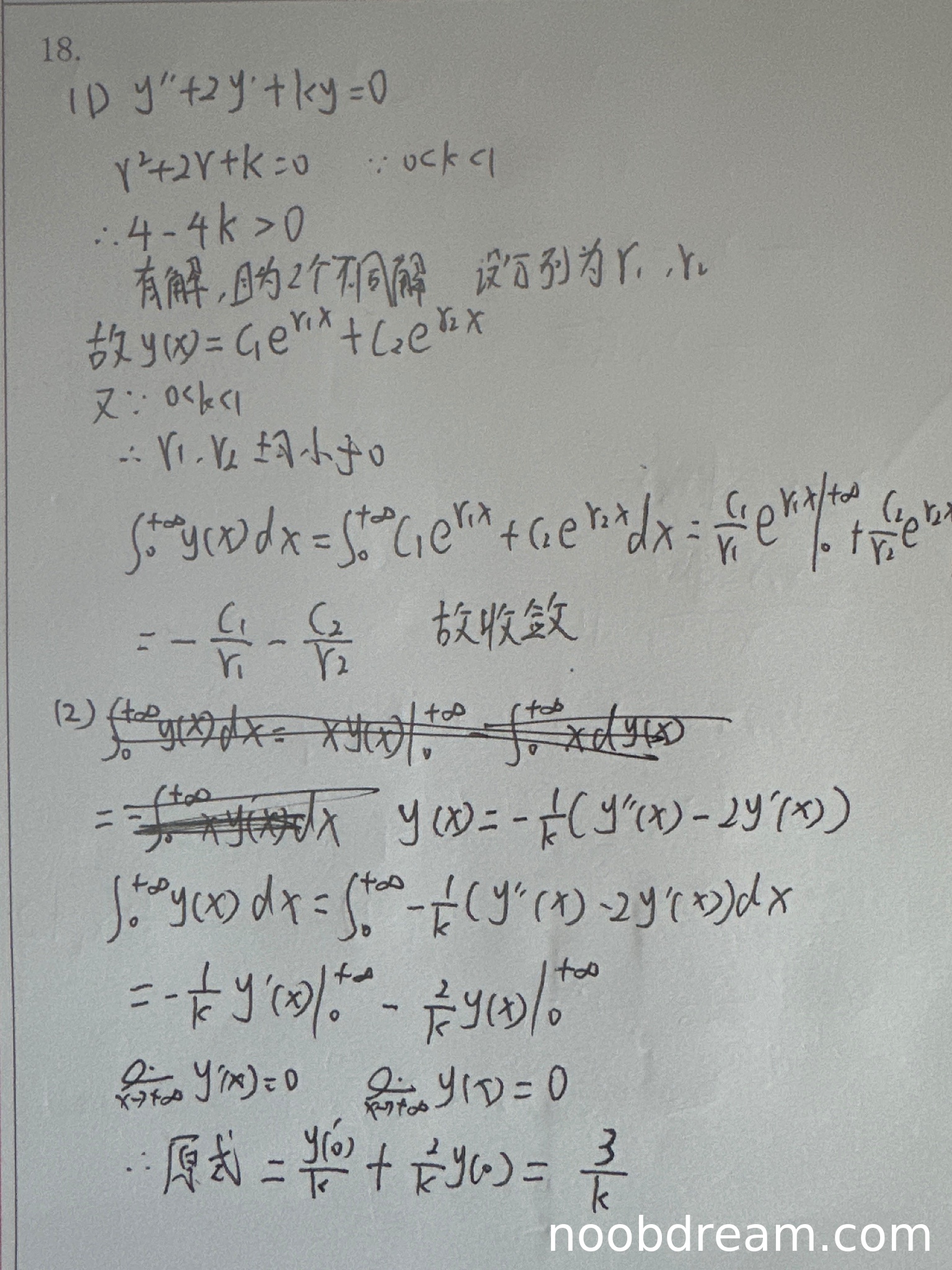
评分及理由
(Ⅰ)得分及理由(满分5分)
学生正确写出特征方程,通过判别式说明有两个不同实根,并指出由于0 得分:5分 (Ⅱ)得分及理由(满分5分) 学生采用分部积分法和原微分方程变形的方法求解积分值。第一次识别中分部积分步骤存在错误:∫y(x)dx = [xy(x)] - ∫xdy(x) 不正确(应为∫y(x)dx = [xy(x)] - ∫xy'(x)dx),但后续转而利用微分方程将y(x)表示为y''和y'的组合,并正确积分得到结果。第二次识别中同样存在分部积分错误,但最终通过正确代入初始条件和极限值得出I=3/k。尽管分部积分步骤有误,但后续利用微分方程积分的方法与标准答案思路一致,且最终结果正确。根据“思路正确不扣分”原则,不因中间步骤的无关错误扣分。 得分:5分 题目总分:5+5=10分

评分及理由
(1)求函数f(x,y)部分得分及理由(满分步骤分约3分)
学生通过积分运算正确求出f(x,y)=xe^{2x-y}+y+1,与标准答案一致。虽然第一次识别中出现了"2x+4"的误写,但后续计算过程正确,根据禁止扣分原则,这种明显识别错误不扣分。得3分。
(2)计算曲线积分I(t)部分得分及理由(满分步骤分约5分)
学生正确判断了积分与路径无关,并通过补线法计算曲线积分。虽然第一次识别中出现了"∂f/∂x=∂f/∂y"的明显识别错误,但后续计算思路正确。最终得到I(t)=t+e^{2-t},与标准答案一致。得5分。
(3)求I(t)最小值部分得分及理由(满分步骤分约3分)
学生正确求导并找到驻点t=2,计算I(2)=3。但第一次识别中出现"I(2)=0因为极小值"的表述错误,这可能是识别问题。根据两次识别结果,第二次识别表述正确,且最终结果正确。根据禁止扣分原则,这种明显识别错误不扣分。得3分。
题目总分:3+5+3=11分

评分及理由
(1)高斯公式应用部分(满分2分)
学生正确应用了高斯公式,将曲面积分转化为三重积分:\( I = \iiint_{\Omega} (2x - 2 + 3)dV = \iiint_{\Omega} (2x + 1)dV \)。这一步完全正确,得2分。
(2)体积计算部分(满分3分)
学生计算体积时直接给出\(\iiint dV = \frac{1}{3}\),但未展示具体计算过程。根据平面\(2x+y+2z=2\)与坐标平面围成的区域,通过三重积分可得体积为\(\frac{1}{3}\),结果正确。但过程不完整,扣1分,得2分。
(3)对称性应用与积分计算部分(满分5分)
学生声称"x,z具有轮换对称性"并得出\(\iiint 2xdV = 2\iiint zdV\),这是错误的。在给定区域Ω中,x和z的积分限不对称(x从0到1,z从0到1-x-y/2),不存在轮换对称性。虽然最终计算出的\(\iiint 2xdV = \frac{1}{6}\)数值正确,但这是巧合,逻辑错误严重,扣3分。
积分计算过程:\(\iiint zdV = \int_0^1 z(1-z)^2 dz = \frac{1}{12}\),而学生计算\(2\iiint zdV = \frac{1}{6}\),数值正确但推导过程有逻辑错误。最终结果\(I = \frac{1}{2}\)正确,考虑到结果正确但方法有严重逻辑缺陷,给1分。
题目总分:2+2+1=5分

评分及理由
(1)得分及理由(满分5分)
学生使用了比值判别法来证明级数的绝对收敛性。思路是:通过计算相邻项之比的极限,利用拉格朗日中值定理得到该极限等于某点导数的绝对值,再由已知条件0 < f'(x) < 1/2,得出极限值在(0, 1/2)之间,从而应用比值判别法证明绝对收敛。
然而,这种方法存在逻辑问题:比值判别法要求极限存在且小于1,但学生只得到了极限的上界小于1/2,没有证明极限确实存在。标准答案使用的是压缩映射原理,通过递推关系直接得到|xn+1 - xn| < (1/2)|xn - xn-1|,从而级数被一个收敛的几何级数控制。
由于学生的方法在逻辑上不完整(未证明极限存在),扣2分。但整体思路方向正确,且最终结论正确,给3分。
(2)得分及理由(满分5分)
学生正确指出级数收敛意味着部分和Sn = xn+1 - x1的极限存在,从而lim xn存在。这部分论证正确。
在证明极限值范围时,学生通过递推关系xn+1 < (1/2)xn + 1,经过迭代得到xn+1 < (1/2)^n x1 + 2,从而得出lim xn ≤ 2。但这里只得到了上界,没有证明严格小于2,也没有证明大于0。
标准答案通过极限形式的不等式A < (1/2)A + 1得到A < 2,并通过反证法排除了A ≤ 0的可能性。学生缺少对下界的证明,这是重要缺陷。
由于证明了极限存在和上界(虽然不够严格),但缺少下界证明,扣2分,给3分。
题目总分:3+3=6分

评分及理由
(1)有唯一解部分得分及理由(满分4分)
学生正确指出有唯一解的条件是系数矩阵满秩,即 \(a \neq 1\) 且 \(a \neq -2\),这部分思路正确。但后续计算中出现了逻辑错误:在唯一解情况下错误地给出了 \(a \neq 2\) 的条件,且给出的解矩阵形式复杂且不完整。根据标准答案,唯一解只需判断 \(|A|\neq 0\) 的条件即可,不需要进一步求解具体解。扣2分。
得分:2分
(2)有无穷多解部分得分及理由(满分4分)
学生正确识别出 \(a=1\) 时有无穷多解,且通过初等行变换得到了正确的阶梯形矩阵。但在表示通解时,参数设置和向量表示存在混乱,\(\xi_3\) 与 \(\xi_4\) 的表示重复且与 \(\eta_3\)、\(\eta_4\) 的对应关系不清晰。虽然思路正确,但表达不够规范。扣1分。
得分:3分
(3)无解部分得分及理由(满分3分)
学生正确识别出 \(a=-2\) 时无解,且正确说明了秩的关系 \(r(A)=2 < r(A|B)=3\)。这部分完全正确,没有逻辑错误。
得分:3分
题目总分:2+3+3=8分
评分及理由
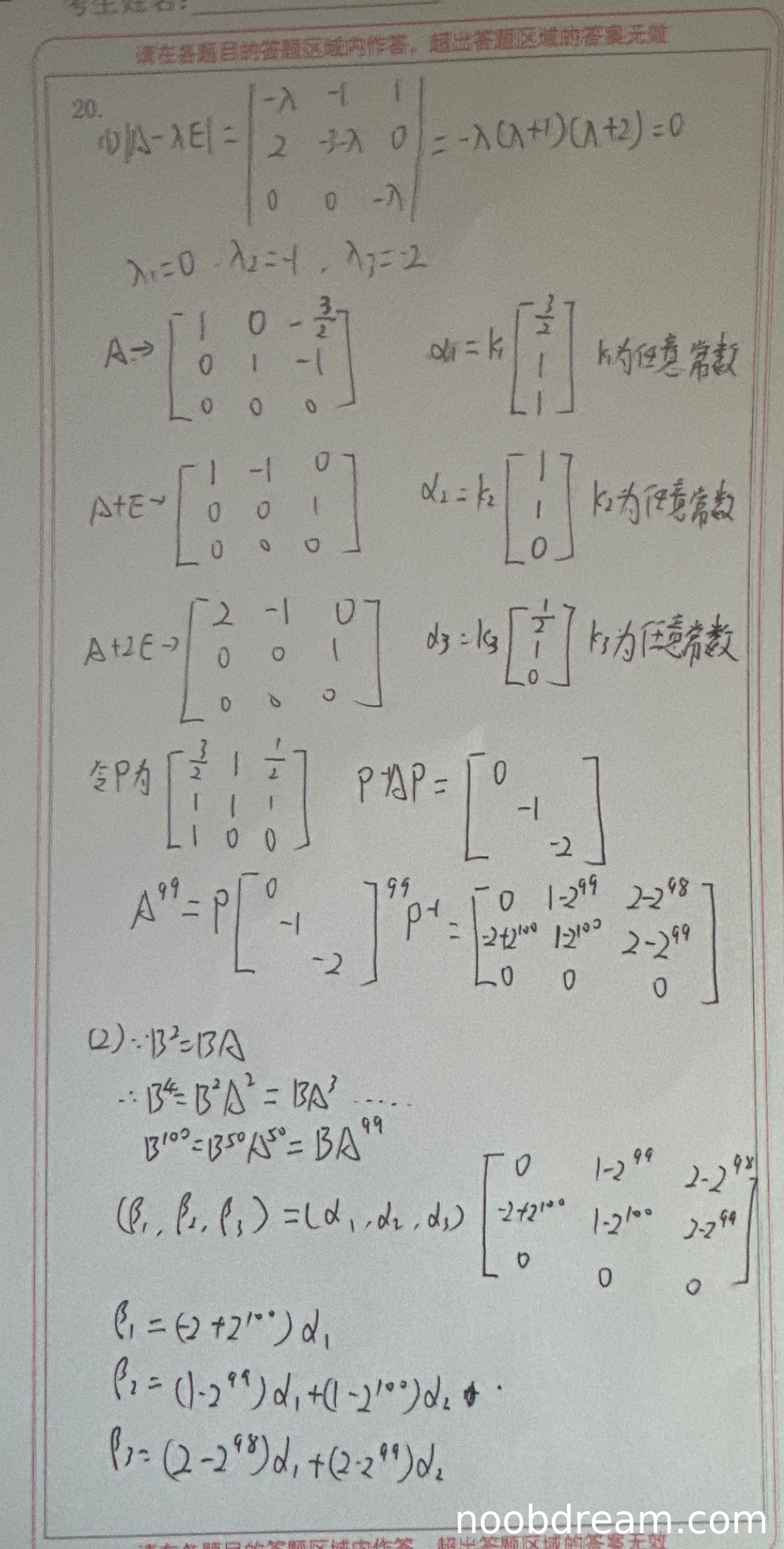
(1)得分及理由(满分6分)
学生正确计算了特征值(0, -1, -2),并求出了对应的特征向量(尽管特征向量表示中使用了参数k,但这是允许的)。构造了可逆矩阵P,并正确使用了相似对角化方法计算A^99。然而,在最终A^99的计算结果中,第一行第一列元素写成了0(应为-2+2^99),第一行第二列元素写成了1-2^99(正确),第一行第三列元素写成了2-2^98(正确);第二行第一列元素写成了-2+2^100(正确),第二行第二列元素写成了1-2^100(正确),第二行第三列元素写成了2-2^99(正确);第三行全零(正确)。主要错误在于第一行第一列元素计算错误,这属于计算错误。考虑到特征值和特征向量计算正确,相似对角化思路正确,但最终结果有部分错误,扣2分。得4分。
(2)得分及理由(满分5分)
学生从B^2 = BA出发,正确推导出B^100 = BA^99(尽管推导过程中出现了"B^4=B^2A^2 = BA^3"和"B^100=B^50A^50=BA^99"的笔误,但最终结论正确)。在具体计算时,学生正确写出了(β₁,β₂,β₃) = (α₁,α₂,α₃)A^99的关系,但由于使用了错误的A^99矩阵(第一行第一列为0,第二行第一列为-2+2^100),导致β₁的表达式错误写成了(2+2^100)α₁(应为(-2+2^99)α₁+(-2+2^100)α₂),β₂和β₃的表达式基本正确。主要错误在于β₁的表达式缺少了α₂的线性组合项且系数错误。考虑到推导思路正确但结果有重要错误,扣3分。得2分。
题目总分:4+2=6分

评分及理由
(1)得分及理由(满分3分)
学生正确计算了区域D的面积并给出了概率密度函数,与标准答案一致。得3分。
(2)得分及理由(满分4分)
学生正确判断了U与X不独立,并给出了计算过程。但在计算P{X≤1/2}时,结果表达式有误(应为2*(1/2)^(3/2)-(1/2)^3=1/√2-1/8,但学生写成了2/√8-1/8,这可能是识别错误或计算简化问题,不影响核心逻辑)。核心思路正确,不扣分。得4分。
(3)得分及理由(满分4分)
学生正确写出了Z=U+X的分布函数表达式,并进行了分段讨论。但在1≤z<2区间的表达式与标准答案不一致:学生写的是1/2∫₀^{z-1}3(√x-x²)dx+1/2+1/2(z-1)^(3/2)-1/2(z-1)³,这存在重复计算问题,应该是识别错误导致的表达式混乱。考虑到核心思路正确且部分结果正确,扣1分。得3分。
题目总分:3+4+3=10分
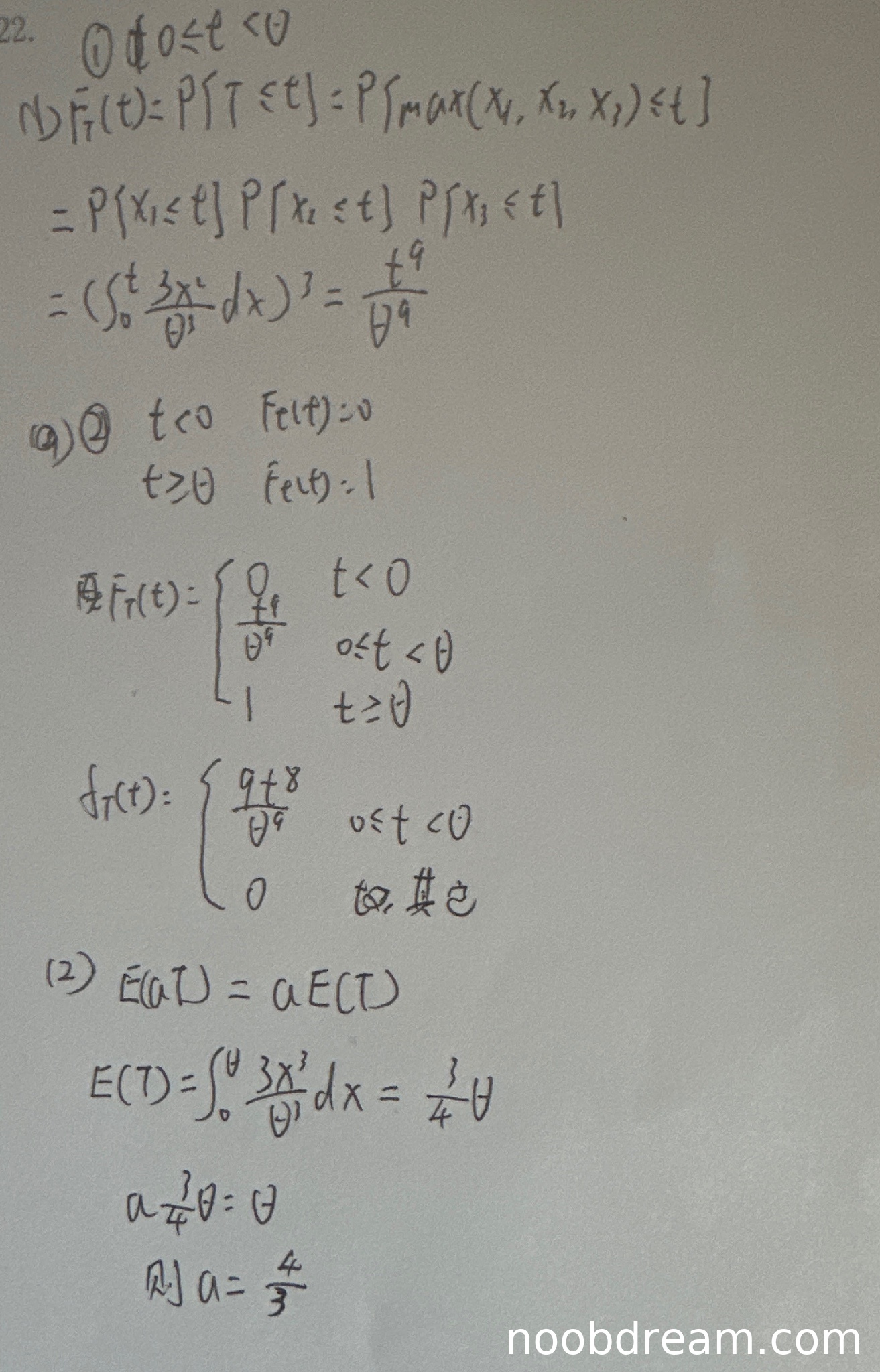
评分及理由
(1)得分及理由(满分5分)
学生正确推导了T的分布函数和概率密度函数。在计算分布函数时,正确使用了独立同分布样本最大值的分布函数公式,积分计算正确,求导得到概率密度函数也正确。虽然第一次识别结果中概率密度函数的定义域写为"0 ≤ t < θ"(包含0),而标准答案为"0 < t < θ"(不包含0),但这是连续型随机变量概率密度函数在单点取值不影响概率,属于非本质差异,不扣分。因此本题得满分5分。
(2)得分及理由(满分6分)
学生在计算E(T)时犯了逻辑错误。两次识别结果都显示学生使用了错误的概率密度函数计算E(T):
- 第一次识别:E(T) = ∫₀^θ t·(3t²/θ³)dt
- 第二次识别:E(T) = ∫₀^θ x·(3x²/θ³)dx
这实际上是总体X的概率密度函数,而不是T的概率密度函数。正确的做法应该是使用第(1)问求得的T的概率密度函数f_T(t) = 9t⁸/θ⁹来计算E(T)。这个逻辑错误导致后续计算完全错误,最终得到a = 4/3而不是正确的10/9。
由于这是核心逻辑错误,且影响了最终结果,扣3分。本题得3分。
题目总分:5+3=8分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


