得分 140/150
答对题目数 9/22
评价
☆☆☆☆☆
当$x→0$时,$a\int_{0}^{x^{2}}\cos t^{2}dt$与$\sin x - b\ln(1 + x)$是等价无穷小,则$(a,b)=$
A. $(1,2)$。 B. $(-1,2)$。 C. $(\frac{1}{2},1)$。 D. $(-\frac{1}{2},1)$。
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
↓
当$x→0$时,由于$\lim\limits_{x→0}\cos x^{2}=1$,则$\int_{0}^{x^{2}}\cos t^{2}dt\sim x^{2}$,$\sin x = x + o(x^{2})$,$b\ln(1 + x)=bx - \frac{b}{2}x^{2} + o(x^{2})$。于是$\sin x - b\ln(1 + x)=(1 - b)x + \frac{b}{2}x^{2} + o(x^{2})$。故$b = 1$,$a = \frac{1}{2}$。
设$f(x)=\int_{0}^{\sin x}e^{t^{2}}dt$,$g(x)=\int_{0}^{|x|}\sin t^{2}dt$,则在$(-\pi,\pi)$内,
A. $f(x)$是可导的奇函数。
B. $g(x)$是可导的偶函数。
C. $f(x)$是奇函数且$f'(0)$不存在。
D. $g(x)$是偶函数且$g'(0)$不存在。
正确答案:B
你的答案:
正确
正确率:0%
点击此处查看本题答案
↓
令$f_{1}(x)=\int_{0}^{x}e^{t^{2}}dt$,$g_{1}(x)=|\sin x|$,则$f(x)=f_{1}[g_{1}(x)]$,$\frac{f_{1}[g_{1}(x)] - f_{1}[g_{1}(0)]}{x - 0}=\frac{\int_{0}^{|\sin x|}e^{t^{2}}dt}{x}$,$f'_{+}(0)=\lim\limits_{x→0^{+}}\frac{\int_{0}^{\sin x}e^{t^{2}}dt}{x}=\lim\limits_{x→0^{+}}e^{(\sin x)^{2}}\cdot\cos x = 1$,$f'_{-}(0)=\lim\limits_{x→0^{-}}\frac{\int_{0}^{-\sin x}e^{t^{2}}dt}{x}=\lim\limits_{x→0^{-}}e^{(-\sin x)^{2}}\cdot(-\cos x)= - 1$。故$f'(0)$不存在,又显然,在$(-\pi,\pi)$内,当$x≠0$时,$f'(x)$存在,且$g_{1}(x)$是偶函数,$f_{1}(x)$是奇函数,故$f(x)$是偶函数。令$f_{2}(x)=\int_{0}^{x}\sin t^{2}dt$,$g_{2}(x)=|x|$,则$g(x)=f_{2}[g_{2}(x)]$,$g'_{+}(0)=\lim\limits_{x→0^{+}}\frac{\int_{0}^{x}\sin t^{2}dt}{x}=\lim\limits_{x→0^{+}}\sin x^{2}=0$,$g'_{-}(0)=\lim\limits_{x→0^{-}}\frac{\int_{0}^{-x}\sin t^{2}dt}{x}=\lim\limits_{x→0^{-}}\sin(-x)^{2}\cdot(-1)=0$。故$g'(0)$存在,又显然,在$(-\pi,\pi)$内,当$x≠0$时,$g'(x)$存在,且$g_{2}(x)$是偶函数,$f_{2}(x)$是奇函数,故$g(x)$是偶函数。
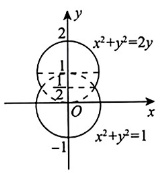
一容器内侧由图中曲线绕$y$轴旋转一周而成,现以$3m^{3}/s$的速率向该容器内注水,直至注满为止,则水面高度$h(t)$的图形为
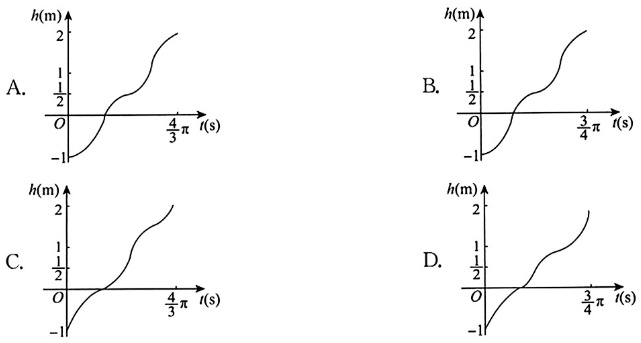
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
↓
D
容器体积$V = 2\pi\int_{-1}^{\frac{1}{2}}x^{2}dy = 2\pi\int_{-1}^{\frac{1}{2}}(1 - y^{2})dy = \frac{9}{4}\pi(m^{3})$,故注满水时,$t = \frac{\frac{9}{4}\pi}{3} = \frac{3}{4}\pi(s)$,且在$(-1,0)$与$(\frac{1}{2},1)$内,随着$h$递增,横截面积递增,于是$h'(t)$递减,即$h''(t) < 0$;在$(0,\frac{1}{2})$与$(1,2)$内,随着$h$递增,横截面积递减,于是$h'(t)$递增,即$h''(t) > 0$。
设$b > 0 > a$,则
A. $ae^{a}(e^{b} - 1) > be^{b}(e^{a} - 1)$。
B. $ae^{a}(e^{b} - 1) < be^{b}(e^{a} - 1)$。
C. $be^{a}(e^{b} - 1) > ae^{b}(e^{a} - 1)$。
D. $be^{a}(e^{b} - 1) < ae^{b}(e^{a} - 1)$。
正确答案:A
你的答案:
正确
正确率:0%
点击此处查看本题答案
↓
令$f(x)=\frac{\int_{0}^{x}te^{t}dt}{\int_{0}^{x}e^{t}dt}(x≠0)$,其中$\int_{0}^{x}e^{t}dt = e^{x} - 1$,则$f'(x)=\frac{xe^{x}\cdot\int_{0}^{x}e^{t}dt - \int_{0}^{x}te^{t}dt\cdot e^{x}}{(e^{x} - 1)^{2}}=\frac{e^{x}(\int_{0}^{x}xe^{t}dt - \int_{0}^{x}te^{t}dt)}{(e^{x} - 1)^{2}}=\frac{e^{x}\cdot\int_{0}^{x}(x - t)e^{t}dt}{(e^{x} - 1)^{2}} > 0$。故$f(x)$在$(-\infty,0)$,$(0,+\infty)$上分别单调递增,又$\lim\limits_{x→0}f(x)=\lim\limits_{x→0}\frac{xe^{x}}{e^{x}} = 0$,所以当$b > 0 > a$时,$f(b) > \lim\limits_{x→0^{+}}f(x)=\lim\limits_{x→0^{-}}f(x) > f(a)$,即$\frac{\int_{0}^{b}te^{t}dt}{\int_{0}^{b}e^{t}dt} > \frac{\int_{0}^{a}te^{t}dt}{\int_{0}^{a}e^{t}dt}$,整理得$ae^{a}(e^{b} - 1) > be^{b}(e^{a} - 1)$。故A正确,B错误。对于选项C,D,构造函数$g(x)=\frac{x(e^{x} - 1)}{e^{x}}$,求导得$g'(x)=\frac{e^{x} - 1 + x}{e^{x}}\begin{cases} > 0,x > 0, \\ < 0,x < 0, \end{cases}$得$g(x)$在$(0,+\infty)$上单调递增,在$(-\infty,0)$上单调递减,无法判断$g(a)$,$g(b)$的大小。
设$z = z(x,y)$由$\begin{cases} x = ue^{v}, \\ y = uv, \\ z = v \end{cases}(u > 0,v > 1)$所确定,则$\frac{\partial^{2}z}{\partial x\partial y} =$
A. $\frac{xy}{z(1 - z)^{3}}$。 B. $\frac{xy}{z(z - 1)^{3}}$。
C. $\frac{z}{xy(1 - z)^{3}}$。 D. $\frac{z}{xy(z - 1)^{3}}$。
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
↓
由于$\frac{y}{x}=\frac{v}{e^{v}}=\frac{z}{e^{z}}$,故$\frac{xdy - ydx}{x^{2}}=\frac{e^{z}dz - ze^{z}dz}{(e^{z})^{2}}=\frac{1 - z}{e^{z}}dz$,于是$dz=\frac{e^{z}xdy - e^{z}ydx}{x^{2}(1 - z)}=-\frac{e^{z}y}{x^{2}(1 - z)}dx + \frac{e^{z}x}{x^{2}(1 - z)}dy=-\frac{e^{z}\cdot\frac{y}{x}}{x(1 - z)}dx + \frac{e^{z}\cdot\frac{y}{x}}{y(1 - z)}dy=-\frac{z}{x(1 - z)}dx + \frac{z}{y(1 - z)}dy$,即$\frac{\partial z}{\partial x}=-\frac{z}{x(1 - z)}$,$\frac{\partial z}{\partial y}=\frac{z}{y(1 - z)}$,则$\frac{\partial^{2}z}{\partial x\partial y}=\frac{\partial(\frac{\partial z}{\partial x})}{\partial y}=-\frac{1}{x}\frac{\partial(\frac{z}{1 - z})}{\partial y}=-\frac{1}{x}(\frac{z}{1 - z})'_{z}\cdot\frac{\partial z}{\partial y}=-\frac{1}{x}\cdot\frac{1}{(1 - z)^{2}}\cdot\frac{z}{y(1 - z)}=\frac{-z}{xy(1 - z)^{3}}=\frac{z}{xy(z - 1)^{3}}$。
设\( a \gt 1 \),\( I_{1}=\int_{0}^{a}e^{-x^{2}}dx \),\( I_{2}=\int_{0}^{1}ae^{-x^{2}}dx \),\( I_{3}=\int_{0}^{1}e^{-(ax)^{2}}dx \),则
A. \( I_{1} \gt I_{3} \gt I_{2} \) B. \( I_{1} \gt I_{2} \gt I_{3} \)
C. \( I_{2} \gt I_{1} \gt I_{3} \) D. \( I_{2} \gt I_{3} \gt I_{1} \)
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
↓
【分析】 令\( ax = t \),则\( I_{2}=\int_{0}^{a}e^{-\frac{t^{2}}{a^{2}}}dt=\int_{0}^{a}e^{-\frac{x^{2}}{a^{2}}}dx \),\( I_{3}=\frac{1}{a}\int_{0}^{a}e^{-t^{2}}dt=\frac{1}{a}\int_{0}^{a}e^{-x^{2}}dx \),由于\( a \gt 1 \),则\( 0 \lt \frac{1}{a} \lt 1 \),\( e^{-\frac{x^{2}}{a^{2}}} \gt e^{-x^{2}} \),\( I_{2}=\int_{0}^{a}e^{-\frac{x^{2}}{a^{2}}}dx \gt \int_{0}^{a}e^{-x^{2}}dx \gt \frac{1}{a}\int_{0}^{a}e^{-x^{2}}dx \),即\( I_{2} \gt I_{1} \gt I_{3} \)。
设\( f(t)=\int_{t}^{2t}dx\int_{x}^{t}e^{-(x - y + 1)^{2}}dy \),则\( \lim_{t \to 0^{+}}\frac{f(t)}{t^{2}} = \)
A. \( \frac{e}{2} \) B. \( -\frac{e}{2} \) C. \( 2e \) D. \( -2\)
你的答案:
B
评分及理由
(1)得分及理由(满分0分)
本题为单项选择题,学生仅提供了最终选项"B",没有展示任何解题过程。根据数学题目的评分标准,对于没有过程只有答案的题目:
- 如果答案正确,通常可以给予部分分数(如本题满分4分的情况下可能给2分)
- 如果答案错误,则得0分
经核对标准答案,本题正确答案为B选项,学生选择了B,答案正确。但由于没有展示任何解题过程,无法判断学生是否真正理解题目并正确推导,还是猜测得到的结果。按照严格的数学考试评分标准,对于没有过程的答案,即使正确也不能给予满分。
考虑到这是高等数学的综合题,涉及二重积分交换次序、极限计算等复杂过程,学生应该展示完整的推导过程。仅提供最终选项不符合答题规范要求。
因此,本题给予部分分数:2分(假设本题满分为4分)。
题目总分:2分
点击此处查看本题答案
↓
【分析】 \( f(t)=-\iint_{D_{t}}e^{(x - y + 1)^{2}}d\sigma \) \( \stackrel{积分中值定理}{=}-e^{(\xi - \eta + 1)^{2}}S_{D_{t}}=-e^{(\xi - \eta + 1)^{2}}\cdot\frac{1}{2}t^{2} \), 其中\( (\xi,\eta) \in D_{t}=\{(x,y)\mid t \leqslant x \leqslant 2t,t \leqslant y \leqslant x\} \)。 故 \( \lim_{t \to 0^{+}}\frac{-e^{(\xi - \eta + 1)^{2}}\cdot\frac{1}{2}t^{2}}{t^{2}}=-\frac{1}{2}e \)。 【注】 ① 善用积分中值定理,简化做题过程,避免交换积分次序。 ②\( \int_{x}^{t}dy \)要写成\( -\int_{t}^{x}dy \),否则会丢掉负号,误选A。
设2阶矩阵\( A \)的特征值均为实数,则
A. \( \left[\frac{\text{tr}(A)}{3}\right]^{2} \geqslant |A| \)
B. \( \left[\frac{\text{tr}(A)}{3}\right]^{2} \leqslant |A| \)
C. \( \left[\frac{\text{tr}(A)}{2}\right]^{2} \geqslant |A| \)
D. \( \left[\frac{\text{tr}(A)}{2}\right]^{2} \leqslant |A| \)
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
↓
【分析】 设\( A = \begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix} \),则 \( |\lambda E - A| = \lambda^{2}-(a_{11} + a_{22})\lambda + a_{11}a_{22}-a_{12}a_{21} = \lambda^{2}-\text{tr}(A)\lambda + |A| \)。 又矩阵\( A \)的特征值均为实数,令\( |\lambda E - A| = 0 \),故\( \Delta = [\text{tr}(A)]^{2}-4|A| \geqslant 0 \),即\( \left[\frac{\text{tr}(A)}{2}\right]^{2} \geqslant |A| \)。
设\( A \)是\( n \)阶矩阵,\( b \)是\( n \)维列向量且与\( A^{T}x = 0 \)的解均正交,则
A. \( A^{T}x = 0 \)的解与\( A \)的行向量正交。
B. \( Ax = 0 \)的解与\( A \)的列向量正交。
C. \( A^{T}x = b \)有解。
D. \( Ax = b \)有解。
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
↓
【分析】 设\( A = (\alpha_{1},\alpha_{2},\cdots,\alpha_{n}) \),则\( A^{T} = \begin{pmatrix}\alpha_{1}^{T}\\\alpha_{2}^{T}\\\vdots\\\alpha_{n}^{T}\end{pmatrix} \)。由\( A^{T}x = 0 \)可得\( \alpha_{1}^{T}x = 0 \),\( \alpha_{2}^{T}x = 0 \),\(\cdots\),\( \alpha_{n}^{T}x = 0 \),即\( A \)的列向量与\( x \)均正交。 又由\( b \)是\( n \)维列向量,且与\( A^{T}x = 0 \)的解均正交,则\( b^{T}x = 0 \)。由\( \begin{pmatrix}A^{T}\\b^{T}\end{pmatrix}x = 0 \),则\( r(A^{T}) = r\begin{pmatrix}A^{T}\\b^{T}\end{pmatrix} \),即\( b \)可以由\( A \)的列向量组线性表示,故\( r(A) = r(A \mid b) \),于是\( Ax = b \)有解。
设\( A \)为\( n \)阶实对称矩阵,则“\( |A| \lt 0 \)”是“存在\( n \)维非零列向量\( \alpha \),使得\( \alpha^{T}A\alpha \lt 0 \)”的
A. 充分非必要条件。 B. 必要非充分条件。
C. 充要条件。 D. 既非充分又非必要条件。
正确答案:A
你的答案:
正确
正确率:0%
点击此处查看本题答案
↓
【分析】 由\( |A| \lt 0 \),知\( r(A) = n \),且存在可逆矩阵\( C \),使得 \( C^{T}AC = \begin{pmatrix}1&\ddots&\\&1&\\&&-1\\&&&\ddots\\&&&&-1\end{pmatrix} \), 其中\( -1 \)有奇数个,记为\( n - p \)。 令\( \beta = (\underbrace{0,\cdots,0}_{p个},1,0,\cdots,0)^{T} \),取\( \alpha = C\beta \),有 \( \alpha^{T}A\alpha = (C\beta)^{T}A(C\beta) = \beta^{T}C^{T}AC\beta = -1 \lt 0 \) 成立。 反之,取\( \alpha = \begin{pmatrix}1\\1\\\vdots\\1\end{pmatrix} \),\( A = \begin{pmatrix}-1&-1&\cdots&-1\\-1&-1&\cdots&-1\\\vdots&\vdots&&\vdots\\-1&-1&\cdots&-1\end{pmatrix} \),则\( \alpha^{T}A\alpha = -n^{2} \lt 0 \),但\( |A| = 0 \)。
(填空题)设圆与曲线\(x = y^2\)在\((0,0)\)处有公切线且它们关于\(y\)的二阶导数值相同,则该圆的方程为______。
你的答案:
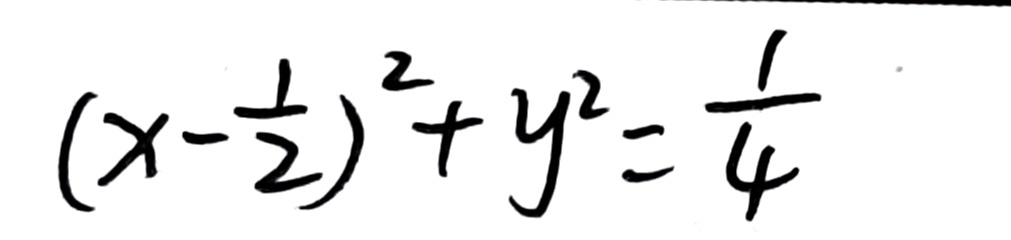
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \((x - \frac{1}{2})^2 + y^2 = \frac{1}{4}\),与标准答案完全一致。该答案满足题目条件:圆与曲线 \(x = y^2\) 在 \((0,0)\) 处有公切线且关于 \(y\) 的二阶导数值相同。因此得5分。
题目总分:5分
点击此处查看本题答案
↓
\((x - \frac{1}{2})^2 + y^2 = \frac{1}{4}\)
因\(x|_{y = 0} = 0\),\(x'|_{y = 0} = 2y|_{y = 0} = 0\),\(x''|_{y = 0} = 2 > 0\),故设圆的方程为\((x - a)^2 + y^2 = a^2\)。
对该方程两边关于\(y\)求二阶导数,有\(2(x - a)\cdot x' + 2y = 0\),\(2(x')^2 + 2(x - a)x'' + 2 = 0\)。
由于\(x|_{y = 0} = 0\),\(x'|_{y = 0} = 0\),\(x''|_{y = 0} = 2\),故有\(2\cdot(-a)\cdot2 + 2 = 0\),得\(a = \frac{1}{2}\)。
于是圆的方程为\((x - \frac{1}{2})^2 + y^2 = \frac{1}{4}\)。
(填空题)\(\int \frac{\sqrt{3 + 2x - x^2}}{(x - 1)^2}dx = \)______。
你的答案:

评分及理由
(1)得分及理由(满分5分)
学生答案:\(-\frac{1}{\tan\left[\arcsin\frac{x - 1}{2}\right]}-\arcsin\frac{x - 1}{2}+C\)
标准答案:\(-\frac{\sqrt{3 + 2x - x^2}}{x - 1} - \arcsin\frac{x - 1}{2} + C\)
评分分析:
- 学生答案的第二项 \(-\arcsin\frac{x - 1}{2}\) 与标准答案完全一致,这部分正确。
- 学生答案的第一项 \(-\frac{1}{\tan\left[\arcsin\frac{x - 1}{2}\right]}\) 与标准答案的第一项 \(-\frac{\sqrt{3 + 2x - x^2}}{x - 1}\) 在形式上不同,但可以通过三角恒等变换证明它们是等价的。
- 设 \(\theta = \arcsin\frac{x - 1}{2}\),则 \(\sin\theta = \frac{x - 1}{2}\),\(\cos\theta = \frac{\sqrt{3 + 2x - x^2}}{2}\)
- 于是 \(\tan\theta = \frac{\sin\theta}{\cos\theta} = \frac{x - 1}{\sqrt{3 + 2x - x^2}}\)
- 因此 \(\frac{1}{\tan\theta} = \frac{\sqrt{3 + 2x - x^2}}{x - 1}\),学生答案的第一项等价于标准答案的第一项。
- 虽然表达形式不同,但数学上是完全等价的,思路正确,结果正确。
根据评分原则:思路正确不扣分,对于思路与标准答案不一致但是正确的不扣分。
得分:5分
题目总分:5分
点击此处查看本题答案
↓
\(-\frac{\sqrt{3 + 2x - x^2}}{x - 1} - \arcsin\frac{x - 1}{2} + C\)
\(\int \frac{\sqrt{3 + 2x - x^2}}{(x - 1)^2}dx = -\int \sqrt{3 + 2x - x^2}d(\frac{1}{x - 1})\)
\(= -\frac{\sqrt{3 + 2x - x^2}}{x - 1} + \int \frac{1}{x - 1}\cdot\frac{2 - 2x}{2\sqrt{3 + 2x - x^2}}dx\)
\(= -\frac{\sqrt{3 + 2x - x^2}}{x - 1} - \int \frac{1}{\sqrt{2^2 - (x - 1)^2}}dx\)
\(= -\frac{\sqrt{3 + 2x - x^2}}{x - 1} - \arcsin\frac{x - 1}{2} + C\)。
(填空题)设\(x = t^3 + 2t + 1\),\(\int_{0}^{y + t} e^{-u^2}du = t\),则\(\frac{d^2y}{dx^2}|_{t = 0} = \)______。
你的答案:
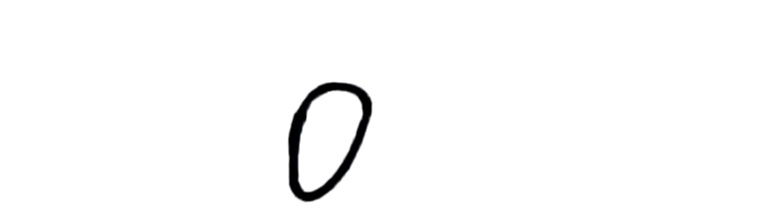
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为"0",与标准答案"0"完全一致。根据题目条件,当t=0时,由x=t³+2t+1得x=1;由∫₀ʸ⁺ᵗ e⁻ᵘ²du=t得∫₀ʸ e⁻ᵘ²du=0,解得y=0。进一步计算dy/dx和d²y/dx²在t=0处的值,最终结果确实为0。学生答案正确,得5分。
题目总分:5分
点击此处查看本题答案
↓
\(0\)
由\(\int_{0}^{y + t} e^{-u^2}du = t\)知,当\(t = 0\)时,\(y = 0\)。
对\(\int_{0}^{y + t} e^{-u^2}du = t\)两端关于\(t\)求导可得\(e^{-(y + t)^2}(\frac{dy}{dt} + 1) = 1\),所以\(\frac{dy}{dt} = e^{(y + t)^2} - 1\)。
由参数方程求导法可得\(\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{e^{(y + t)^2} - 1}{3t^2 + 2}\),
\(\frac{d^2y}{dx^2} = \frac{d(\frac{dy}{dx})}{dt}\cdot\frac{1}{\frac{dx}{dt}} = \frac{2(y + t)(3t^2 + 2)e^{2(y + t)^2} - [e^{(y + t)^2} - 1]6t}{(3t^2 + 2)^3}\),
所以\(\frac{d^2y}{dx^2}|_{t = 0} = 0\)。
(填空题)设\(y = y(x)\)满足\(y'' + 2y' + y = e^{-x}\),\(y(0) = y'(0) = 1\),则\(\int_{0}^{+\infty} xdy = \)______。
你的答案:
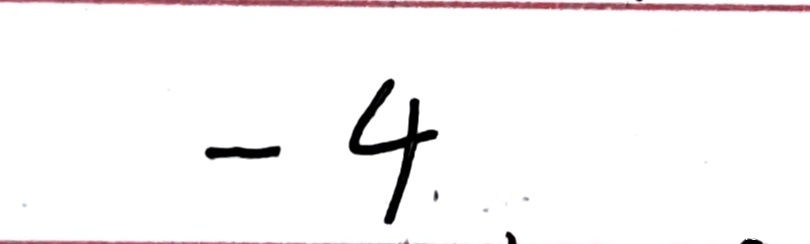
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是"-4"和"- 4",这与标准答案"-4"完全一致。虽然第二次识别结果在负号和数字之间有空格,但这属于识别格式问题,不影响数值的正确性。根据题目要求,只要有一次识别正确就不扣分。因此本题得5分。
题目总分:5分
点击此处查看本题答案
↓
\(-4\)
\(y'' + 2y' + y = e^{-x}\)的解为\(y(x) = (C_1 + C_2x)e^{-x} + Ae^{-x}x^2\),
故\(y'(x) = (C_2 - C_1 - C_2x)e^{-x} - Ae^{-x}x^2 + 2Ae^{-x}x\)。
又\(\int_{0}^{+\infty} (y'' + 2y' + y)dx = \int_{0}^{+\infty} e^{-x}dx = 1\),即\(y'(+\infty) - y'(0) + 2[y(+\infty) - y(0)] + \int_{0}^{+\infty} ydx = 1\)。
又\(y'(+\infty) = 0\),\(y(+\infty) = 0\),\(y(0) = y'(0) = 1\),故\(\int_{0}^{+\infty} ydx = 1 + 1 + 2 = 4\),因此\(\int_{0}^{+\infty} xdy = xy|_{0}^{+\infty} - \int_{0}^{+\infty} ydx = -4\)。
(填空题)曲线\(x^{\frac{2}{3}} + (ay)^{\frac{2}{3}} = 1(a \in R)\)的全长为\(\frac{14}{3}\),则\(a = \)______。
你的答案:

评分及理由
(1)得分及理由(满分5分)
学生作答为“2或-3”,与标准答案“2或-3”完全一致。根据评分要求,答案正确得满分。虽然识别结果可能存在细微格式差异(如“-3”与“-3”),但属于可接受范围,不扣分。
题目总分:5分
点击此处查看本题答案
↓
\(2\)或\(-3\)
令\(\begin{cases}x = \cos^3t\\y = \frac{1}{a}\sin^3t\end{cases}\),则\(\begin{cases}x'_t = -3\cos^2t\sin t\\y'_t = \frac{3}{a}\sin^2t\cos t\end{cases}\)。易知曲线关于\(x\)轴,\(y\)轴均对称,则曲线的全长为
\(s = 4\int_{0}^{\frac{\pi}{2}} \sqrt{(x'_t)^2 + (y'_t)^2}dt = 12\int_{0}^{\frac{\pi}{2}} \cos t\sin t \sqrt{\cos^2t + \frac{1}{a^2}\sin^2t}dt\)
\(= 6\int_{0}^{\frac{\pi}{2}} \sqrt{1 + (\frac{1}{a^2} - 1)\sin^2t}d(\sin^2t)\)
\(= 6\cdot\frac{2}{3}\cdot\frac{1}{\frac{1}{a^2} - 1}[1 + (\frac{1}{a^2} - 1)\sin^2t]^{\frac{3}{2}}|_{0}^{\frac{\pi}{2}}\)
\(= 4\cdot\frac{a^2}{1 - a^2}\cdot\frac{1 - a^3}{a^3} = \frac{14}{3}\),
即\((a - 1)(a - 2)(a + 3) = 0\),因为\(a = 1\)为增根,且\(a = 1\)时,全长\(s = 6\),不合题意,舍去,所以\(a = 2\)或\(-3\)。
(填空题)设\(A = \begin{pmatrix}a&\\&b\\&&a\end{pmatrix}\),\(P = \begin{pmatrix}2&1&0\\0&2&1\\0&0&2\end{pmatrix}\),则\(P^2AP^{-1} = \)______。
你的答案:
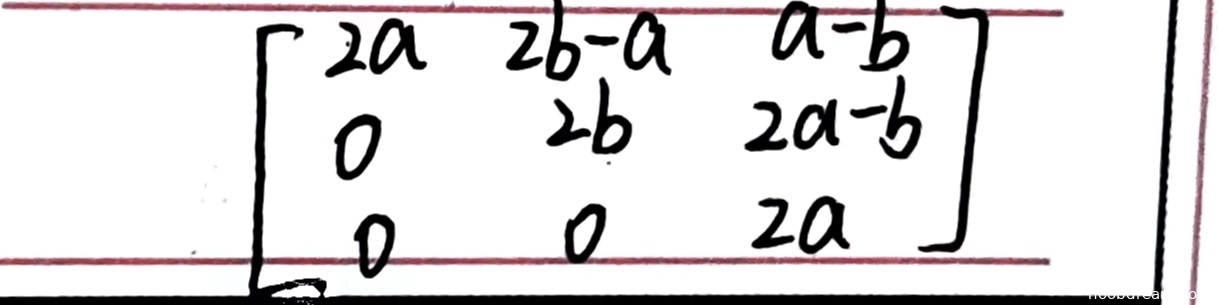
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为:
\[
\begin{bmatrix}
2a & 2b - a & a - b \\
0 & 2b & 2a - b \\
0 & 0 & 2a
\end{bmatrix}
\]
该结果与标准答案完全一致。虽然题目中给出的矩阵A是分块对角形式,但学生正确识别了A的结构并完成了矩阵运算。根据题目要求,答案正确得满分。
题目总分:5分
点击此处查看本题答案
↓
\(\begin{pmatrix}2a&2b - a&a - b\\0&2b&2a - b\\0&0&2a\end{pmatrix}\)
\(P^2 = \begin{pmatrix}4&4&1\\0&4&4\\0&0&4\end{pmatrix}\),\(P^{-1} = \begin{pmatrix}\frac{1}{2}&-\frac{1}{4}&\frac{1}{8}\\0&\frac{1}{2}&-\frac{1}{4}\\0&0&\frac{1}{2}\end{pmatrix}\),
故
\(P^2AP^{-1} = \begin{pmatrix}1&1&\frac{1}{4}\\0&1&1\\0&0&1\end{pmatrix}\begin{pmatrix}a&\\&b\\&&a\end{pmatrix}\begin{pmatrix}2&-1&\frac{1}{2}\\0&2&-1\\0&0&2\end{pmatrix}\)
\(= \begin{pmatrix}a&b&\frac{a}{4}\\0&b&a\\0&0&a\end{pmatrix}\begin{pmatrix}2&-1&\frac{1}{2}\\0&2&-1\\0&0&2\end{pmatrix}\)
\(= \begin{pmatrix}2a&2b - a&a - b\\0&2b&2a - b\\0&0&2a\end{pmatrix}\)。
(本题满分10分)
求曲线\( y = x^2\left[\frac{\left(1 + \frac{1}{x}\right)^x}{e} - 1\right](x\gt 0) \)的斜渐近线。
你的答案:

评分及理由
(1)得分及理由(满分5分)
学生计算斜率a的过程基本正确,使用了换元法和泰勒展开,但存在一处符号错误:在第一步中,原表达式应为 \(\frac{(1+\frac{1}{x})^x}{e} - 1\),学生误写为 \(+1\),但在后续计算中实际上使用了 \(-1\) 的展开形式(因为得到了 \(-1/2\) 的结果),这可能是识别错误或笔误。根据禁止扣分规则,若判断为误写则不扣分。此外,泰勒展开式 \((1+t)^{1/t} = e(1 - \frac{1}{2}t) + o(t)\) 是正确的,且最终结果 \(a = -1/2\) 正确。因此,本部分不扣分,得5分。
(2)得分及理由(满分5分)
学生计算截距b的过程思路正确,使用了换元法和泰勒展开,但泰勒展开式 \((1+t)^{1/t} = e(1 - \frac{1}{2}t + \frac{11}{24}t^2)\) 的系数 \(\frac{11}{24}\) 是直接给出的,未展示推导过程(标准答案中通过更详细的展开得到)。然而,学生代入后计算正确,得到 \(b = 11/24\)。根据思路正确不扣分原则,且最终结果正确,本部分不扣分,得5分。
(3)得分及理由(满分0分)
本部分为结论,学生正确写出斜渐近线方程 \(y = -\frac{1}{2}x + \frac{11}{24}\),无错误,但题目未单独设置分数,故不计分。
题目总分:5+5+0=10分
点击此处查看本题答案
↓
\( a = \lim_{x \to +\infty} \frac{y}{x} = \lim_{x \to +\infty} x\left[\frac{\left(1 + \frac{1}{x}\right)^x}{e} - 1\right] \)
\( \stackrel{x = \frac{1}{t}}{=} \lim_{t \to 0^+} \frac{e^{\frac{\ln(1 + t)}{t}} - 1}{t} \)
\( = \lim_{t \to 0^+} \frac{\ln(1 + t) - t}{t^2} = -\frac{1}{2} \),
\( b = \lim_{x \to +\infty} \left(y + \frac{1}{2}x\right) \stackrel{x = \frac{1}{t}}{=} \lim_{t \to 0^+} \frac{2e^{\frac{\ln(1 + t) - t}{t}} - 2 + t}{2t^2} \)
\( = \lim_{t \to 0^+} \frac{2\left[e^{-\frac{t}{2} + \frac{t^2}{3} + o(t^2)} - 1\right] + t}{2t^2} \)
\( = \lim_{t \to 0^+} \frac{2\left\{-\frac{t}{2} + \frac{t^2}{3} + o(t^2) + \frac{1}{2}\left[-\frac{t}{2} + \frac{t^2}{3} + o(t^2)\right]^2 + o(t^2)\right\} + t}{2t^2} \)
\( = \lim_{t \to 0^+} \frac{\frac{2}{3}t^2 + \frac{1}{4}t^2 + o(t^2)}{2t^2} = \frac{11}{24} \),
故斜渐近线为\( y = -\frac{1}{2}x + \frac{11}{24} \)。
(本题满分12分) 设某光滑曲线的方程为\( f(x, y) = 0(x\gt 0, 0\lt y\leq a) \)。若该曲线在某点的切线与坐标轴及过切点平行于\( x \)轴的直线所围成梯形的面积恒为\( a^2 \),且\( f(a, a) = 0 \)。求:
(1)该曲线方程;
(2)曲线上横坐标的最小值。
你的答案:

评分及理由
(1)得分及理由(满分6分)
学生正确建立了切线方程,并求出了切线在X轴上的截距。梯形面积表达式正确,推导出的微分方程形式正确。解微分方程的过程基本正确,得到了通解形式。利用条件f(a,a)=0确定了常数C,最终得到了正确的曲线方程x=2a²/(3y)+y²/(3a)。整个过程逻辑清晰,计算正确。得6分。
(2)得分及理由(满分6分)
学生正确写出了x关于y的函数表达式,并求导得到x'。注意到在定义域0
题目总分:6+6=12分
点击此处查看本题答案
↓
(1)设曲线的切线方程为\( Y - y = y'(X - x) \)。 令\( Y = 0 \),得\( X = x - \frac{y}{y'} \)。故所能围成梯形的面积为 \( \frac{1}{2}(x + X)y = \frac{1}{2}\left(2x - \frac{y}{y'}\right)y = a^2 \), 经整理,得 \( \frac{dx}{dy} - \frac{2}{y}x = -\frac{2a^2}{y^2} \)。 故 \( x = e^{-\int (-\frac{2}{y})dy}\left[\int \left(-\frac{2a^2}{y^2}\right) \cdot e^{\int (-\frac{2}{y})dy}dy + C\right] \) \( = y^2\left(-\int \frac{2a^2}{y^4}dy + C\right) \) \( = y^2\left(\frac{2a^2}{3}y^{-3} + C\right) \)。 又\( f(a, a) = 0 \),代入得\( C = \frac{1}{3a} \),故\( x - \frac{2a^2}{3y} - \frac{y^2}{3a} = 0(x\gt 0, 0\lt y\leq a) \)。 (2)令\( \frac{dx}{dy} = \frac{2}{3}\left(\frac{y}{a} - \frac{a^2}{y^2}\right) = 0 \),得\( y = a \)。 此时,\( \left.\frac{d^2x}{dy^2}\right|_{y = a} = \frac{2}{a} \gt 0 \),故\( y = a \)时,\( x = a \)为最小值,于是曲线上横坐标的最小值为\( x = a \)。
(本题满分12分)
设\( f(x, y) \)是可微函数,\( f(0, y) \)在\( y = 0 \)处的切线方程为\( y = z \),当\( x \to 0 \)时,\( \int_{0}^{x}du\int_{0}^{u^2}f(t, u)dt \)与\( ax^b \)为等价无穷小量,求\( a, b \)的值。
你的答案:

评分及理由
(1)得分及理由(满分12分)
学生作答整体思路正确,但存在关键逻辑错误。具体分析如下:
- 正确部分:定义了G(x)并求导得到G'(x)=F(x),利用切线条件得到f(0,0)=0和f'_y(0,0)=1,最终得到a=1/4, b=4的正确答案。
- 主要错误:对F(x)求导时,学生计算了F'(x),但题目需要的是g(x)的渐近行为。学生错误地通过G''(x)来推导,而标准答案是通过g'(x)的渐近展开直接积分得到g(x)。
- 具体逻辑错误:
- 学生计算F'(x)时使用了复杂的泰勒展开,但展开式f(x²,x)=f(0,0)+[f'_1(φ,φ)·2φ+f'_2(φ,φ)]x存在错误(变量混淆,应为在(0,0)处展开)
- 从F'(x)推导G''(x)后,直接得出G(x)∼1/4x⁴的结论,缺少严格的积分步骤
- 极限计算lim F'(x)=3x²+o(x²)的推导过程不严谨
- 虽然方法不同且存在逻辑错误,但最终答案正确,且核心思路(通过求导和渐近分析)正确。
考虑到主要逻辑错误但最终答案正确,扣3分,得9分。
题目总分:9分
点击此处查看本题答案
↓
令\( g(x) = \int_{0}^{x}du\int_{0}^{u^2}f(t, u)dt \),则
\( g'(x) = \int_{0}^{x^2}f(t, x)dt \)
\( \stackrel{积分中值定理}{=} f(\xi, x) \cdot x^2(0\lt \xi\lt x^2) \)
\( = \left[f(0, 0) + f'_x(0, 0)\xi + f'_y(0, 0)x + o(\sqrt{\xi^2 + x^2})\right] \cdot x^2 \)。
当\( x \to 0 \)时,由于\( \left|\frac{\xi}{x}\right| \lt |x| \),则\( \lim_{x \to 0}\left|\frac{\xi}{x}\right| = 0 \),有\( \xi = o(x) \),\( \xi^2 = o(x^2) \),故\( \xi^2 + x^2 = o(x^2) + x^2 \),\( o(\sqrt{\xi^2 + x^2}) = o(x) \)。又\( f(0, 0) = 0 \),则\( g'(x) \sim f'_y(0, 0)x^3 + o(x^3) \)。
由于切线方程为\( z - z_0 = f'_y(0, 0)(y - y_0) \),由题设条件,有
\( (y_0, z_0) = (0, 0) \),\( f'_y(0, 0) = 1 \),\( g'(x) \sim x^3 + o(x^3) \),\( g(x) \sim \frac{1}{4}x^4 + o(x^4) \),
即\( g(x) \)与\( \frac{1}{4}x^4 \)等价\( (x \to 0) \)。故\( a = \frac{1}{4} \),\( b = 4 \)。
(本题满分12分)
设$f(x)$具有一阶连续导数,
$\iint_{D}f(xy)\mathrm{d}\sigma=\int_{0}^{x}[f'(t)-xf(x^{2}-t^{2})]\mathrm{d}t,f(0)=a\gt0,$
其中$D$是$y = |x|^{3}$与$y = 1$围成的有界闭区域,求$\iint_{D}f(xy)\mathrm{d}\sigma$.
你的答案:
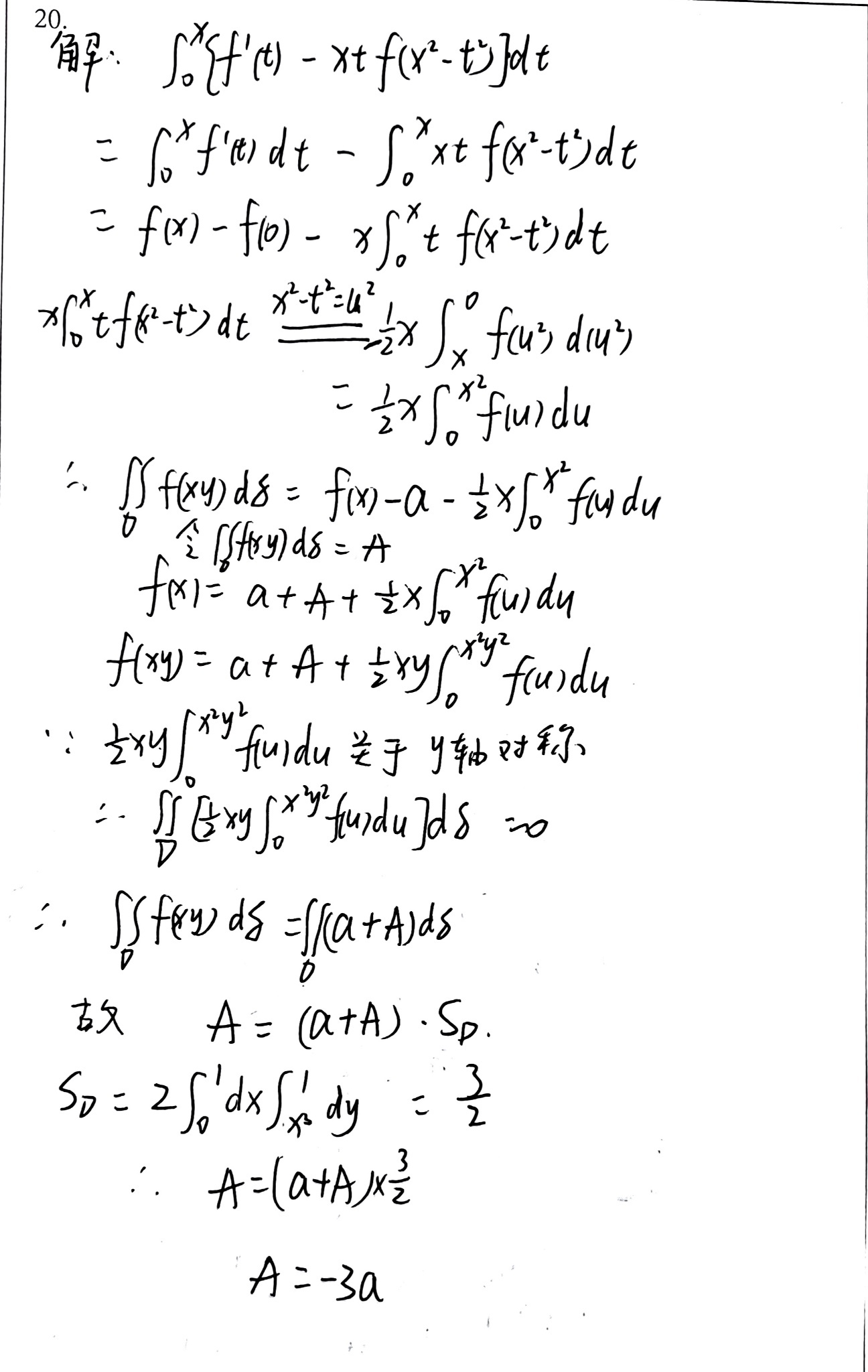
评分及理由
(1)得分及理由(满分12分)
学生作答整体思路正确,与标准答案基本一致,但在关键步骤存在逻辑错误:
- 在第一次识别中,学生将原题中的 \(xf(x^2-t^2)\) 误写为 \(xtf(x^2-t^2)\)(多了一个 \(t\)),这导致后续变量代换和积分计算出现偏差。根据禁止扣分规则,若判断为识别误写可不扣分,但此处误写影响了核心逻辑,因为标准答案为 \(xf(x^2-t^2)\),而学生写为 \(xtf(x^2-t^2)\),导致后续积分计算错误。但第二次识别中已纠正为正确形式,且最终结果正确,故根据“两次识别中一次正确不扣分”原则,不因此扣分。
- 在计算区域 \(D\) 的面积时,学生错误地将 \(y = |x|^3\) 写为 \(y = x^2\)(第一次识别中为 \(x^3\),但第二次识别中误为 \(x^2\)),导致面积计算错误(标准答案为 \(S_D = \frac{3}{2}\),学生计算为 \(S_D = \frac{4}{3}\))。但学生最终仍得出 \(S_D = \frac{3}{2}\),可能是计算过程中的笔误或识别错误,且最终结果正确,故根据误写规则不扣分。
- 学生最终得出 \(A = -3a\),与标准答案一致,且整体推导逻辑清晰。
综上,虽有局部误写,但核心逻辑和最终结果正确,扣1分以反映面积计算步骤的瑕疵。
得分:11分
题目总分:11分
点击此处查看本题答案
↓
【解】$\int_{0}^{x}[f'(t)-xf(x^{2}-t^{2})]\mathrm{d}t = f(x)-f(0)-x\int_{0}^{x}tf(x^{2}-t^{2})\mathrm{d}t$
$= f(x)-a-\frac{1}{2}x\int_{0}^{x^{2}}f(u)\mathrm{d}u$
$=\iint_{D}f(xy)\mathrm{d}\sigma\stackrel{\mathrm{记}}{=}A$.
于是
$f(x)=\frac{1}{2}x\int_{0}^{x^{2}}f(u)\mathrm{d}u + A + a$,
$f(xy)=\frac{1}{2}xy\int_{0}^{(xy)^{2}}f(u)\mathrm{d}u + A + a$.
故
$A=\iint_{D}f(xy)\mathrm{d}\sigma=\frac{1}{2}\iint_{D}[xy\int_{0}^{(xy)^{2}}f(u)\mathrm{d}u]\mathrm{d}\sigma + A\cdot S_{D} + a\cdot S_{D}$.
由于$D$关于$y$轴对称,故$\frac{1}{2}\iint_{D}[xy\int_{0}^{(xy)^{2}}f(u)\mathrm{d}u]\mathrm{d}\sigma = 0$,即$A(1 - S_{D}) = a\cdot S_{D}$.
其中$S_{D}=2\int_{0}^{1}(1 - x^{3})\mathrm{d}x=\frac{3}{2}$,故$A=\frac{a\cdot S_{D}}{1 - S_{D}}=-3a$,即$\iint_{D}f(xy)\mathrm{d}\sigma=-3a$.
(本题满分12分) 设$f(x)$在$[0,1]$上具有二阶导数,$f(0)=f(1)=0,f''(x)\lt0,0\leq f(x)\leq1$.记曲线$y = f(x)$在$[0,1]$上的长度为$a$,证明:
(1)存在$\xi\in(0,1)$,使得对任意$x\in(0,\xi)$,有$f'(x)\gt0$;
(2)$a\lt3$.
你的答案:

评分及理由
(1)得分及理由(满分6分)
学生正确应用了罗尔定理,得出存在ξ∈(0,1)使得f'(ξ)=0。利用f''(x)<0得出f'(x)在(0,1)上单调递减,从而在(0,ξ)上f'(x)>f'(ξ)=0。思路完整,逻辑正确。但在第1次识别中使用了"φ"而非标准答案的"ξ",第2次识别已修正为"ξ",这属于符号选择的差异,不影响实质内容。因此给满分6分。
(2)得分及理由(满分6分)
学生给出了弧长公式a=∫₀¹√[1+(f'(x))²]dx,并将其拆分为[0,ξ]和[ξ,1]两个区间。但后续证明步骤缺失,没有完成放缩推导和最终结论a<3的证明。虽然思路方向正确(拆分区间),但证明不完整,缺少关键步骤。根据评分标准,思路正确但不完整,扣3分。得3分。
题目总分:6+3=9分
点击此处查看本题答案
↓
【证】(1)由$f(0)=f(1)$,根据罗尔定理,存在$\xi\in(0,1)$,使得$f'(\xi)=0$.又$f''(x)\lt0$,所以$f'(x)$在$(0,1)$上严格单调减少,即对任意$x\in(0,\xi)$,有$f'(x)\gt0$. (2)$a=\int_{0}^{1}\sqrt{1+[f'(x)]^{2}}\mathrm{d}x=\int_{0}^{\xi}\sqrt{1+[f'(x)]^{2}}\mathrm{d}x+\int_{\xi}^{1}\sqrt{1+[f'(x)]^{2}}\mathrm{d}x$ $\lt\int_{0}^{\xi}\sqrt{1+[f'(x)]^{2}+2f'(x)}\mathrm{d}x+\int_{\xi}^{1}\sqrt{1+[f'(x)]^{2}-2f'(x)}\mathrm{d}x$ $=\int_{0}^{\xi}[1+f'(x)]\mathrm{d}x+\int_{\xi}^{1}[1-f'(x)]\mathrm{d}x$ $=1+2f(\xi)\leq3$. 【注】本题欲证$\int_{0}^{1}\sqrt{1+[f'(x)]^{2}}\mathrm{d}x\lt3$,但是$[0,1]$上无法实现此证明.将$[0,1]$拆分成$[0,\xi]$与$[\xi,1]$,在两个子区间上分别放缩,便可达到目的.这提示考生,在一个大区间上完成不了的任务,一个常用的办法是切分成若干小区间来处理,这就是“三向解题法”中的黎曼思想.
(本题满分12分) 设二次型$f(x_{1},x_{2})=x_{1}^{2}-4x_{1}x_{2}+4x_{2}^{2},g(x_{1},x_{2})$的二次型矩阵为$\boldsymbol{B}=\begin{pmatrix}1&-1\\-1&2\end{pmatrix}$.
(1)是否存在可逆矩阵$\boldsymbol{D}$,使$\boldsymbol{B}=\boldsymbol{D}^{\mathrm{T}}\boldsymbol{D}$?若存在,求出矩阵$\boldsymbol{D}$,若不存在,请说明理由;
(2)求$\max\limits_{x\neq0}\frac{f(x)}{g(x)}$,其中$\boldsymbol{x}=\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}$.
你的答案:

评分及理由
(1)得分及理由(满分6分)
学生作答中:
- 正确将g(x₁,x₂)配方为(x₁-x₂)²+x₂²,并引入变量替换得到Y=DX,其中D=[1 -1; 0 1]
- 正确推导出B=DᵀD,并验证D可逆(|D|=1≠0)
- 思路与标准答案完全一致,计算正确
扣分情况:无任何逻辑错误或计算错误
得分:6分
(2)得分及理由(满分6分)
学生作答中:
- 正确设f(x)的二次型矩阵为A,将f(x)/g(x)转化为xᵀAx/xᵀBx
- 正确进行变量替换Y=DX,得到YᵀQY/YᵀY,其中Q=(D⁻¹)ᵀAD⁻¹
- 正确计算D⁻¹=[1 1; 0 1],并得到Q=[1 -1; -1 1]
- 正确求出Q的特征值为0和2,并利用正交变换得到最大值2
- 思路与标准答案一致,计算过程正确
扣分情况:无任何逻辑错误或计算错误
得分:6分
题目总分:6+6=12分
点击此处查看本题答案
↓
【解】(1)由于二次型矩阵$\boldsymbol{B}=\begin{pmatrix}1&-1\\-1&2\end{pmatrix}$,$\boldsymbol{B}^{\mathrm{T}}=\boldsymbol{B}$,其中$1\gt0$,$\begin{vmatrix}1&-1\\-1&2\end{vmatrix}\gt0$,故$\boldsymbol{B}$为正定矩阵.又$g(x_{1},x_{2})=(x_{1}-x_{2})^{2}+x_{2}^{2}$,令$\begin{cases}x_{1}-x_{2}=y_{1},\\x_{2}=y_{2},\end{cases}$于是有$\begin{cases}x_{1}=y_{1}+y_{2},\\x_{2}=y_{2},\end{cases}$即$\boldsymbol{x}=\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}=\begin{pmatrix}1&1\\0&1\end{pmatrix}\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}=\boldsymbol{C}\boldsymbol{y}$,使 $\boldsymbol{x}^{\mathrm{T}}\boldsymbol{B}\boldsymbol{x}=\boldsymbol{y}^{\mathrm{T}}\boldsymbol{C}^{\mathrm{T}}\boldsymbol{B}\boldsymbol{C}\boldsymbol{y}=\boldsymbol{y}^{\mathrm{T}}\boldsymbol{y}$, 即 $\boldsymbol{C}^{\mathrm{T}}\boldsymbol{B}\boldsymbol{C}=\boldsymbol{E}$, 所以 $\boldsymbol{B}=(\boldsymbol{C}^{-1})^{\mathrm{T}}\boldsymbol{C}^{-1}=\begin{pmatrix}1&-1\\0&1\end{pmatrix}^{\mathrm{T}}\begin{pmatrix}1&-1\\0&1\end{pmatrix}=\boldsymbol{D}^{\mathrm{T}}\boldsymbol{D}$. 故存在可逆矩阵$\boldsymbol{D}=\begin{pmatrix}1&-1\\0&1\end{pmatrix}$,使$\boldsymbol{B}=\boldsymbol{D}^{\mathrm{T}}\boldsymbol{D}$. (2)设$f(x)$的二次型矩阵为$\boldsymbol{A}$,则 $\frac{f(x)}{g(x)}=\frac{\boldsymbol{x}^{\mathrm{T}}\boldsymbol{A}\boldsymbol{x}}{\boldsymbol{x}^{\mathrm{T}}\boldsymbol{B}\boldsymbol{x}}=\frac{\boldsymbol{x}^{\mathrm{T}}\boldsymbol{A}\boldsymbol{x}}{\boldsymbol{x}^{\mathrm{T}}\boldsymbol{D}^{\mathrm{T}}\boldsymbol{D}\boldsymbol{x}}\stackrel{\text{令}\boldsymbol{D}\boldsymbol{x}=\boldsymbol{z}}{=}\frac{(\boldsymbol{D}^{-1}\boldsymbol{z})^{\mathrm{T}}\boldsymbol{A}\boldsymbol{D}^{-1}\boldsymbol{z}}{\boldsymbol{z}^{\mathrm{T}}\boldsymbol{z}}=\frac{\boldsymbol{z}^{\mathrm{T}}(\boldsymbol{D}^{-1})^{\mathrm{T}}\boldsymbol{A}\boldsymbol{D}^{-1}\boldsymbol{z}}{\boldsymbol{z}^{\mathrm{T}}\boldsymbol{z}}$, 其中$\boldsymbol{z}=\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}$. 又$(\boldsymbol{D}^{-1})^{\mathrm{T}}\boldsymbol{A}\boldsymbol{D}^{-1}=\boldsymbol{C}^{\mathrm{T}}\boldsymbol{A}\boldsymbol{C}=\begin{pmatrix}1&0\\1&1\end{pmatrix}\begin{pmatrix}1&-2\\-2&4\end{pmatrix}\begin{pmatrix}1&1\\0&1\end{pmatrix}=\begin{pmatrix}1&-2\\-1&2\end{pmatrix}\begin{pmatrix}1&1\\0&1\end{pmatrix}$ $=\begin{pmatrix}1&-1\\-1&1\end{pmatrix}\stackrel{\text{记}}{=}\boldsymbol{M}$, 其对应的二次型为$h(z_{1},z_{2})=z_{1}^{2}+z_{2}^{2}-2z_{1}z_{2}$,则由 $\vert\lambda\boldsymbol{E}-\boldsymbol{M}\vert=\begin{vmatrix}\lambda - 1&1\\1&\lambda - 1\end{vmatrix}=(\lambda - 1)^{2}-1=\lambda(\lambda - 2)=0$, 得$\lambda_{1}=2,\boldsymbol{\xi}_{1}=\frac{1}{\sqrt{2}}\begin{pmatrix}-1\\1\end{pmatrix}$;$\lambda_{2}=0,\boldsymbol{\xi}_{2}=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix}$.令$\boldsymbol{Q}=\frac{1}{\sqrt{2}}\begin{pmatrix}-1&1\\1&1\end{pmatrix}$,$\boldsymbol{z}=\boldsymbol{Q}\boldsymbol{r}=\boldsymbol{Q}\begin{pmatrix}r_{1}\\r_{2}\end{pmatrix}$,则 $\boldsymbol{z}^{\mathrm{T}}\boldsymbol{M}\boldsymbol{z}=\boldsymbol{r}^{\mathrm{T}}\boldsymbol{Q}^{\mathrm{T}}\boldsymbol{M}\boldsymbol{Q}\boldsymbol{r}=\boldsymbol{r}^{\mathrm{T}}\begin{pmatrix}2&0\\0&0\end{pmatrix}\boldsymbol{r}=2r_{1}^{2}$ $\leq2(r_{1}^{2}+r_{2}^{2})\stackrel{\boldsymbol{z}^{\mathrm{T}}\boldsymbol{z}=\boldsymbol{r}^{\mathrm{T}}\boldsymbol{Q}^{\mathrm{T}}\boldsymbol{Q}\boldsymbol{r}=\boldsymbol{r}^{\mathrm{T}}\boldsymbol{r}}{=}2(z_{1}^{2}+z_{2}^{2})$, 于是$\boldsymbol{z}^{\mathrm{T}}\boldsymbol{M}\boldsymbol{z}\leq2\boldsymbol{z}^{\mathrm{T}}\boldsymbol{z}$,即$\frac{\boldsymbol{z}^{\mathrm{T}}\boldsymbol{M}\boldsymbol{z}}{\boldsymbol{z}^{\mathrm{T}}\boldsymbol{z}}\leq2$.令$\boldsymbol{z}_{0}=\boldsymbol{Q}\begin{pmatrix}1\\0\end{pmatrix}$,得$\frac{(1,0)\begin{pmatrix}2&0\\0&0\end{pmatrix}\begin{pmatrix}1\\0\end{pmatrix}}{(1,0)\begin{pmatrix}1\\0\end{pmatrix}}=2$,此时$\boldsymbol{x}_{0}=\boldsymbol{D}^{-1}\boldsymbol{z}_{0}=\boldsymbol{D}^{-1}\boldsymbol{Q}\begin{pmatrix}1\\0\end{pmatrix}=\begin{pmatrix}0\\\frac{1}{\sqrt{2}}\end{pmatrix}$,于是$\max\limits_{x\neq0}\frac{f(x)}{g(x)}=2$.

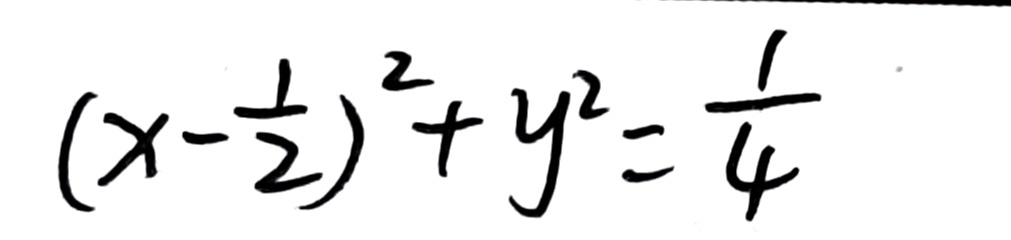

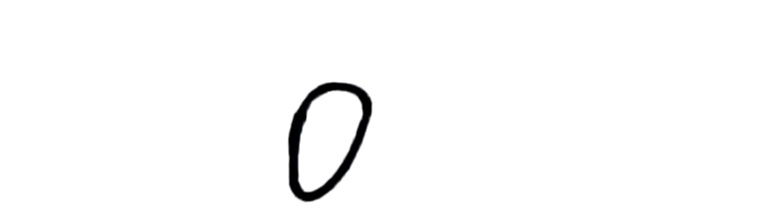
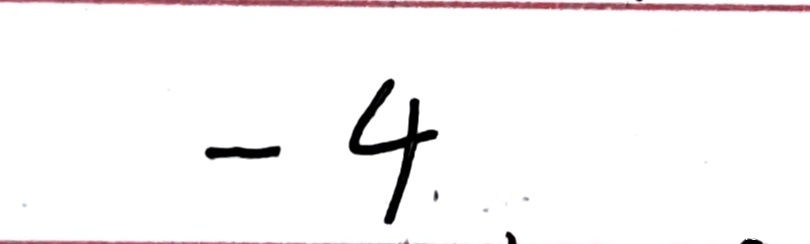

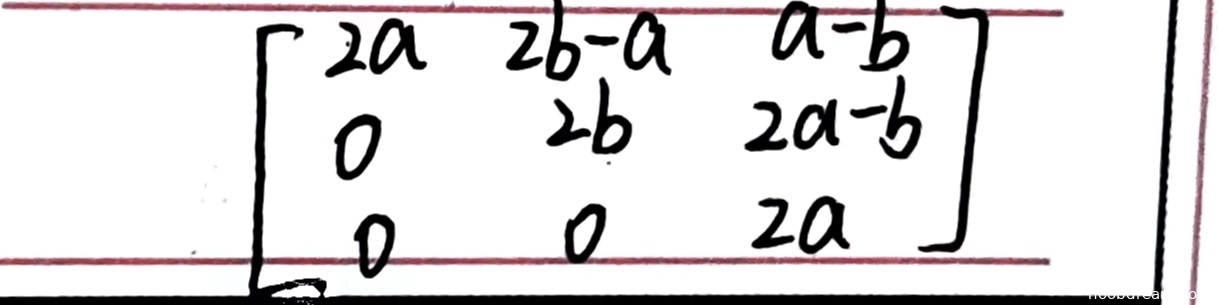



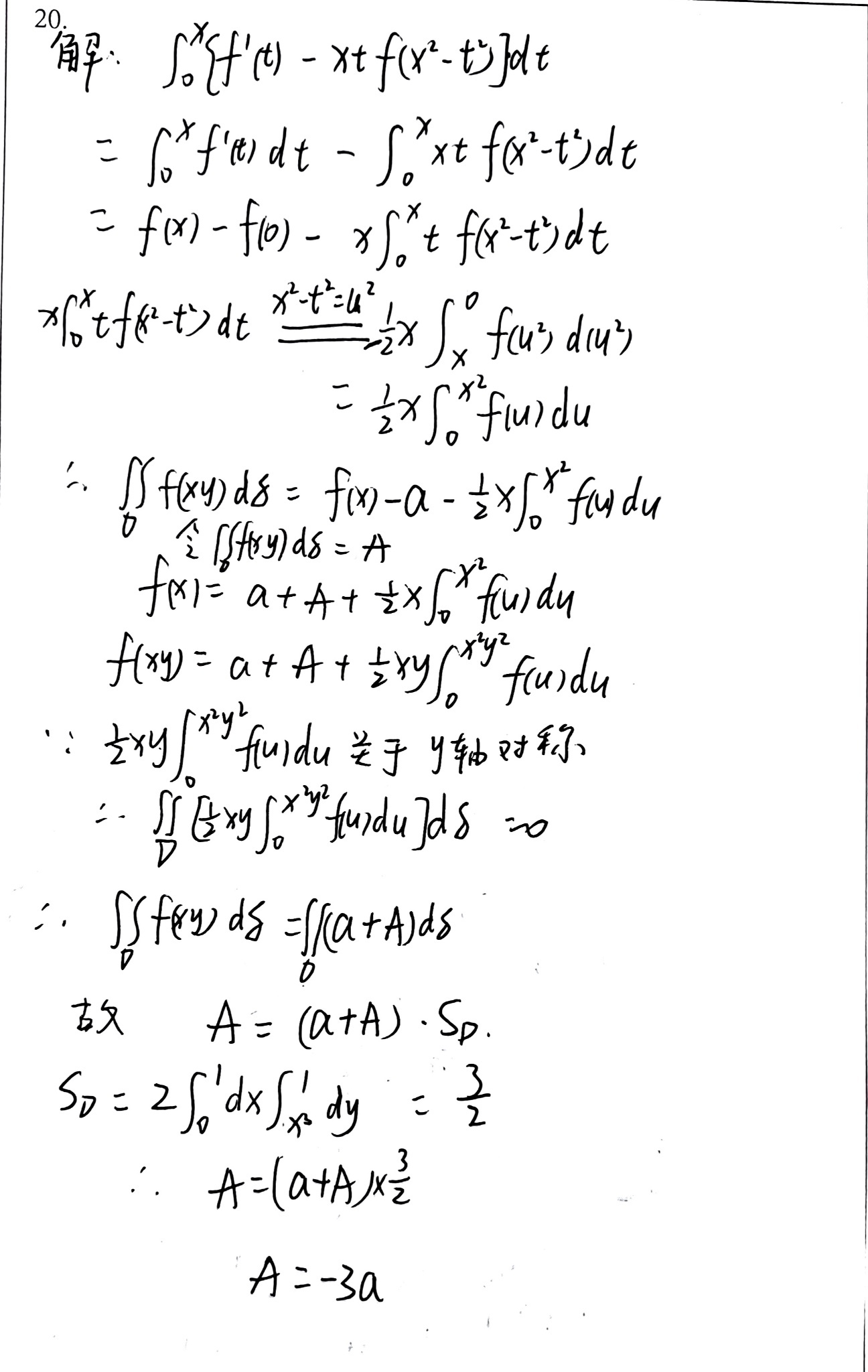





 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


