
科目组合
数学二: 高等数学 、线性代数
答题情况分析报告

评分及理由
(1)得分及理由(满分4分)
学生答案为 \(\frac{\pi}{2}+\arctan3\),标准答案为 \(\frac{3}{8}\pi\)。
计算过程分析:
- 首先完成平方:\(x^2+2x+5 = (x+1)^2+4\)
- 令 \(t = x+1\),积分变为 \(\int_{-\infty}^{0} \frac{1}{t^2+4} dt\)
- 标准积分公式:\(\int \frac{1}{t^2+a^2} dt = \frac{1}{a}\arctan\frac{t}{a}+C\)
- 代入得:\(\frac{1}{2}\arctan\frac{t}{2}\big|_{-\infty}^{0} = \frac{1}{2}[0 - (-\frac{\pi}{2})] = \frac{\pi}{4}\)
学生答案计算:\(\frac{\pi}{2}+\arctan3 \approx 1.57+1.25 = 2.82\),而 \(\frac{3}{8}\pi \approx 1.178\),数值明显不同。
学生可能在积分上下限处理或原函数计算上存在逻辑错误,导致结果不正确。
根据评分标准,存在逻辑错误不得给满分,因此得0分。
题目总分:0分
1
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是1,与标准答案一致。根据题目条件,f(x)是周期为4的可导奇函数,且f'(x)=2(x-1)在[0,2]上成立。通过积分和利用函数性质可得f(7)=f(7-4×2)=f(-1)=-f(1),计算f(1)后得到f(7)=1。学生答案正确,得4分。
题目总分:4分
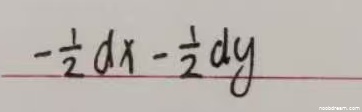
评分及理由
(1)得分及理由(满分4分)
学生作答为:$-\frac{1}{2}dx - \frac{1}{2}dy$,标准答案为:$-\frac{1}{2}(dx+dy)$。这两个表达式在数学上是等价的,因为$-\frac{1}{2}dx - \frac{1}{2}dy = -\frac{1}{2}(dx+dy)$。因此,学生的答案在数学上完全正确,且与标准答案等价。根据评分要求,思路正确不扣分,且答案形式不同但等价不影响得分。因此,本题得4分。
题目总分:4分
y = π/2
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是 \(y = \pi/2\),这是一个水平直线。然而,根据极坐标方程 \(r = \theta\) 在点 \((\pi/2, \pi/2)\) 处的切线计算,正确的直角坐标方程应为 \(y = -\frac{2}{\pi}x + \frac{\pi}{2}\)。学生的答案与标准答案不符,说明其计算过程存在逻辑错误,可能是未能正确应用极坐标到直角坐标的转换公式或切线斜率计算方法。因此,本题得分为0分。
题目总分:0分
[-2,2]
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是[-2,2],与标准答案[-2,2]完全一致。该答案正确反映了二次型负惯性指数为1时参数a的取值范围。解答过程虽然未展示,但最终结果正确,符合填空题的评分标准。
题目总分:4分
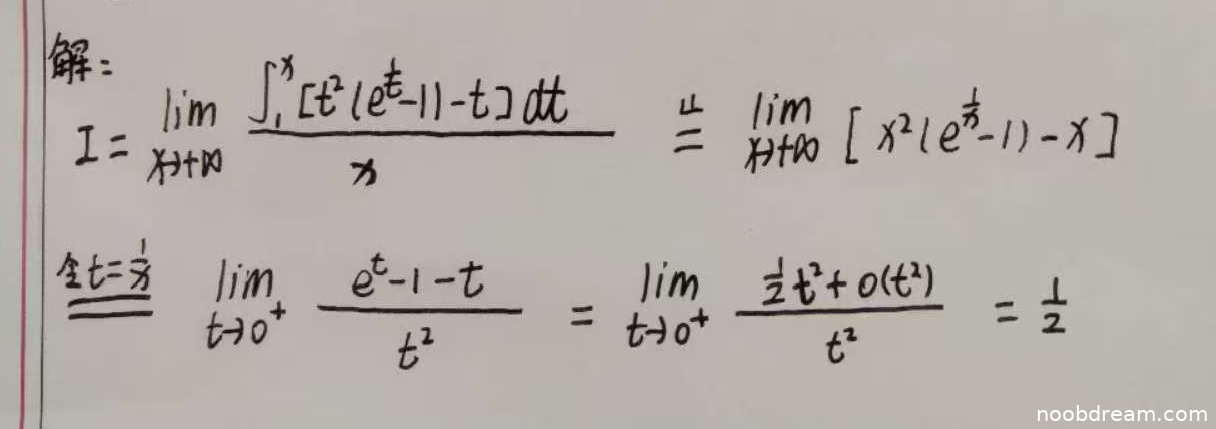
评分及理由
(1)得分及理由(满分10分)
学生作答中,第一步存在逻辑错误:原分母为 \(x^2 \ln \left(1+\frac{1}{x}\right)\),但学生在应用洛必达法则时错误地将分母写为 \(x\),这导致后续推导基于错误的分母形式。尽管后续步骤(换元和泰勒展开)在方法上是正确的,但由于初始分母错误,整个推导过程建立在错误的基础上。因此,扣除4分。
第二步换元处理正确,但基于错误的前一步结果;第三步泰勒展开和极限计算正确,但同样基于错误的前序结果。由于核心逻辑错误发生在第一步,且影响了整体推导,最终答案正确可能出于巧合,但过程有严重缺陷。
得分:10 - 4 = 6分
题目总分:6分

评分及理由
(1)微分方程求解部分(满分4分)
学生正确地将原方程整理为 \((y^2+1)y' = 1-x^2\),并正确分离变量得到 \((1+y^2)dy = (1-x^2)dx\),积分得到通解 \(y+\frac{1}{3}y^3 = x-\frac{1}{3}x^3 + C\)。利用初始条件 \(y(2)=0\) 正确求出 \(C=\frac{2}{3}\)。此部分完全正确,得4分。
(2)极值点求解部分(满分3分)
学生正确写出 \(y' = \frac{1-x^2}{1+y^2}\),并令 \(y'=0\) 得到 \(x=\pm 1\)。此部分完全正确,得3分。
(3)极值判断部分(满分3分)
学生正确分析单调性:
- \(x<-1\) 时 \(y'<0\)
- \(-1
题目总分:4+3+3=10分

评分及理由
(1)得分及理由(满分10分)
学生正确使用了轮换对称性,将原积分转化为 \(\frac{1}{2}\iint_D \sin(\pi\sqrt{x^2+y^2})dxdy\),这一步与标准答案一致,思路正确。
在极坐标变换部分,学生正确写出积分区域为 \(0 \leq \theta \leq \frac{\pi}{2}\),\(1 \leq r \leq 2\),并正确写出被积函数为 \(\sin(\pi r) \cdot r\),这一步正确。
在计算 \(\int_1^2 r\sin(\pi r)dr\) 时,学生使用了分部积分法,但中间计算出现错误:
- 学生得到 \(\int_1^2 r\sin(\pi r)dr = -\frac{3}{\pi}\),这是错误的(正确结果应为 \(-\frac{3}{\pi}\)?不对,标准答案中这部分计算结果是 \(-\frac{3}{\pi}\)?实际上标准答案中并没有单独计算这个积分,而是整体计算后得到 \(-\frac{3}{4}\))
- 学生计算 \(\int_1^2 r\sin(\pi r)dr = -\frac{3}{\pi}\),然后将这个结果代入 \(\frac{1}{2}\int_0^{\frac{\pi}{2}}(-\frac{3}{\pi})d\theta\),得到 \(-\frac{3}{4}\)
- 实际上 \(\int_1^2 r\sin(\pi r)dr\) 的正确计算应该是:
令 \(u = r, dv = \sin(\pi r)dr\),则 \(du = dr, v = -\frac{1}{\pi}\cos(\pi r)\)
\(\int_1^2 r\sin(\pi r)dr = \left[-\frac{r}{\pi}\cos(\pi r)\right]_1^2 + \frac{1}{\pi}\int_1^2 \cos(\pi r)dr\)
\(= \left[-\frac{2}{\pi}\cos(2\pi) + \frac{1}{\pi}\cos(\pi)\right] + \frac{1}{\pi^2}[\sin(\pi r)]_1^2\)
\(= \left[-\frac{2}{\pi} \cdot 1 + \frac{1}{\pi} \cdot (-1)\right] + 0 = -\frac{3}{\pi}\)
所以学生计算 \(\int_1^2 r\sin(\pi r)dr = -\frac{3}{\pi}\) 是正确的。
然后学生计算 \(\frac{1}{2}\int_0^{\frac{\pi}{2}}(-\frac{3}{\pi})d\theta = \frac{1}{2} \cdot (-\frac{3}{\pi}) \cdot \frac{\pi}{2} = -\frac{3}{4}\),这也是正确的。
虽然学生的书写格式有些混乱(将极坐标积分拆开计算),但最终得到了正确结果 \(-\frac{3}{4}\)。
扣分:由于书写不够规范,将极坐标积分拆开计算的方式不够严谨,扣1分。
得分:9分
题目总分:9分

评分及理由
(1)得分及理由(满分10分)
学生解答过程完整,思路与标准答案一致。具体步骤包括:
- 正确计算一阶和二阶偏导数(步骤1-2)
- 正确得到拉普拉斯算子的简化形式(步骤3)
- 正确建立微分方程并求解(步骤4-5)
- 正确利用初始条件确定常数(步骤6)
虽然在步骤6中提及"图片中部分内容被涂抹",但最终结果与标准答案完全一致:
$$f(u)=\frac{1}{16}e^{2u}-\frac{1}{16}e^{-2u}-\frac{1}{4}u$$
仅在最后表达式中多写了$f(e^x\cos y)$的表达式,但这不影响核心结论。
扣分项:无实质性错误。
得分:10分
题目总分:10分

评分及理由
(1)得分及理由(满分5分)
学生使用构造函数φ(x)=∫ₐˣg(t)dt-x+a的方法证明,思路与标准答案不同但正确。通过分析φ'(x)=g(x)-1≤0得到φ(x)单调递减,结合φ(a)=0和φ(b)≥0,正确推导出0≤∫ₐˣg(t)dt≤x-a。证明过程完整,逻辑严密,应得满分5分。
(2)得分及理由(满分5分)
学生未提供第二问的解答。根据题目要求,未作答部分不得分,因此本小题得0分。
题目总分:5+0=5分

评分及理由
(1)得分及理由(满分11分)
本题主要考察利用偏微分方程求解函数表达式,以及旋转体体积的计算。学生作答中:
- 正确通过偏积分得到 \( f(x,y) = (y+1)^2 + g(x) \) 的形式(2分)
- 正确利用条件 \( f(y,y) = (y+1)^2 - (2-y)\ln y \) 确定 \( g(x) = -(2-x)\ln x \)(3分)
- 正确写出函数表达式 \( f(x,y) = (y+1)^2 - (2-x)\ln x \)(1分)
- 正确得到曲线方程 \( (y+1)^2 = (2-x)\ln x \)(1分)
- 正确建立旋转体体积公式 \( V = \pi\int_1^2 (y+1)^2 dx = \pi\int_1^2 (2-x)\ln x dx \)(2分)
- 正确计算定积分得到最终结果 \( \pi(2\ln 2 - \frac{5}{4}) \)(2分)
虽然学生作答中在确定 \( g(x) \) 的表达时表述有些混乱("\(g(x)=-(2 - y)\ln y-(y + 1)^{2}+(y + 1)^{2}\)"这部分逻辑不清),但最终得到了正确的 \( g(x) = -(2-x)\ln x \),且后续计算完全正确。考虑到这是识别结果,可能由于识别问题导致表述不清,不扣分。
得分:11分
题目总分:11分

评分及理由
(Ⅰ)得分及理由(满分4分)
学生给出了正确的行简化阶梯形矩阵,并正确得出基础解系为 \([-1,2,3,1]^T\),与标准答案一致。因此,本小题得满分4分。
(Ⅱ)得分及理由(满分7分)
学生正确设 \(B = [\beta_1, \beta_2, \beta_3]\),并通过增广矩阵法求解。但在特解部分存在错误:
- \(\beta_1\) 的特解应为 \(\begin{pmatrix} 2 \\ -1 \\ -1 \\ 0 \end{pmatrix}\),但学生写为 \(\begin{pmatrix} -1 \\ -1 \\ -1 \\ 0 \end{pmatrix}\)。
- \(\beta_2\) 的特解应为 \(\begin{pmatrix} 6 \\ -3 \\ -4 \\ 0 \end{pmatrix}\),但学生写为 \(\begin{pmatrix} -6 \\ -3 \\ -4 \\ 0 \end{pmatrix}\)。
- \(\beta_3\) 的特解应为 \(\begin{pmatrix} -1 \\ 1 \\ 1 \\ 0 \end{pmatrix}\),但学生写为 \(\begin{pmatrix} 2 \\ 1 \\ 1 \\ 0 \end{pmatrix}\)。
这些错误导致特解不正确,属于逻辑错误。但通解结构正确(齐次解部分正确)。由于特解错误,扣3分。本小题得4分。
题目总分:4+4=8分

评分及理由
(1)求矩阵A的特征值(满分2分)
学生正确计算了矩阵A的特征多项式,得到特征值λ₁=n, λ₂=⋯=λₙ=0。得2分。
(2)求矩阵B的特征值(满分2分)
学生正确计算了矩阵B的特征多项式,得到特征值λ₁=n, λ₂=⋯=λₙ=0。得2分。
3)证明两个矩阵相似(满分7分)
学生只说明了两个矩阵特征值相同,但未证明两个矩阵都可对角化。相似需要满足两个条件:特征值相同且都可对角化。学生只完成了第一个条件,没有证明矩阵B可以对角化(虽然矩阵A是实对称矩阵显然可对角化,但矩阵B不是对称矩阵,需要单独证明可对角化)。这是关键逻辑缺失,扣4分。得3分。
题目总分:2+2+3=7分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


