
科目组合
数学一: 高等数学 、线性代数 、概率论
答题情况分析报告
-1
评分及理由
(1)得分及理由(满分4分)
学生直接给出了答案"-1",与标准答案完全一致。由于本题为填空题,不要求展示解题过程,因此直接写出正确答案即可得满分。虽然学生未展示计算过程,但根据填空题的评分标准,答案正确即可获得全部分数。
题目总分:4分
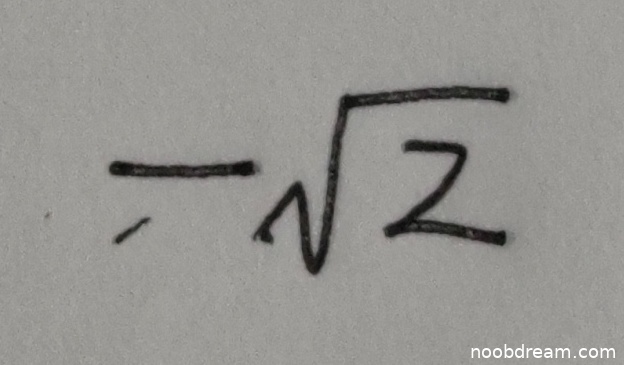
评分及理由
(1)得分及理由(满分4分)
学生最终答案为 $-\sqrt{2}$,与标准答案完全一致。虽然题目给出了参数方程,需要计算二阶导数 $\frac{d^{2}y}{dx^{2}}$ 在 $t=1$ 处的值,但学生直接给出了正确结果。根据评分要求,答案正确应给满分。识别过程中第一次识别结果为空,但第二次识别结果正确,根据规则"只要其中有一次回答正确则不扣分",故得4分。
题目总分:4分
n+am
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是"n+am",与标准答案"n + am"完全一致。该题目是求解满足给定二阶线性微分方程和初始条件的函数在0到正无穷的积分,学生答案正确反映了通过拉普拉斯变换或特征方程法求解后得到的结果。答案形式正确,系数和符号均无误,因此得满分4分。
题目总分:4分
e
评分及理由
(1)得分及理由(满分4分)
该题要求学生计算函数 \(f(x, y)=\int_{0}^{x y} e^{x t^{2}} dt\) 在点 \((1,1)\) 处的混合偏导数 \(\frac{\partial^{2} f}{\partial x \partial y}\) 的值。学生的答案为 "e"。
首先分析正确解法:
设 \(u = xy\),则 \(f(x,y) = \int_0^u e^{x t^2} dt\)。
先求 \(\frac{\partial f}{\partial y}\):
由莱布尼茨公式,\(\frac{\partial f}{\partial y} = e^{x(xy)^2} \cdot x + \int_0^{xy} \frac{\partial}{\partial y}(e^{x t^2}) dt\)。
由于被积函数 \(e^{x t^2}\) 与 \(y\) 无关,第二项为0,所以 \(\frac{\partial f}{\partial y} = x e^{x^3 y^2}\)。
再求 \(\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial}{\partial x}(x e^{x^3 y^2})\):
应用乘积法则:\(\frac{\partial}{\partial x}(x e^{x^3 y^2}) = e^{x^3 y^2} + x \cdot e^{x^3 y^2} \cdot 3x^2 y^2 = e^{x^3 y^2}(1 + 3x^3 y^2)\)。
代入 \((1,1)\) 得:\(\left.\frac{\partial^{2} f}{\partial x \partial y}\right|_{(1,1)} = e^{1}(1 + 3) = 4e\)。
学生答案 "e" 与标准答案 \(4e\) 不符,存在计算错误。虽然学生可能正确识别了指数函数部分,但忽略了乘积法则中的其他项,导致结果不完整。根据评分要求,答案错误应得0分。
题目总分:0分
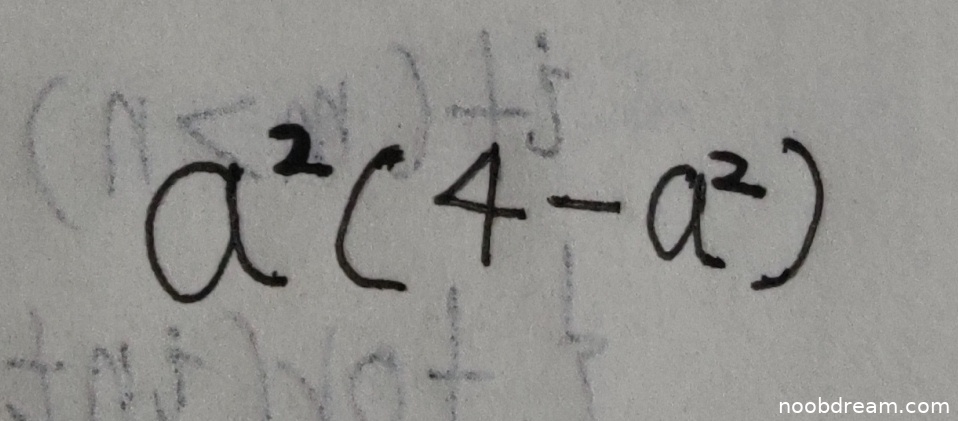
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是 \(a^{2}(4 - a^{2})\),展开后为 \(4a^{2} - a^{4}\),即 \(-a^{4} + 4a^{2}\)。标准答案为 \(a^{4} - 4a^{2}\),两者相差一个负号。由于行列式的计算可能因展开方式不同而出现符号差异,但这里学生答案与标准答案在代数表达式形式上不一致(符号相反),属于计算错误。因此,该答案不能得分。
题目总分:0分
2π
评分及理由
(1)得分及理由(满分4分)
学生给出的答案是 \(2\pi\),而标准答案是 \(\frac{2}{\pi}\)。计算过程如下:
- \(X \sim U(-\frac{\pi}{2}, \frac{\pi}{2})\),概率密度函数为 \(f_X(x) = \frac{1}{\pi}\)
- 协方差公式:\(\operatorname{Cov}(X,Y) = E[XY] - E[X]E[Y]\)
- \(E[X] = 0\)(均匀分布对称性)
- \(E[Y] = E[\sin X] = \int_{-\pi/2}^{\pi/2} \sin x \cdot \frac{1}{\pi} dx = 0\)
- \(E[XY] = E[X\sin X] = \int_{-\pi/2}^{\pi/2} x\sin x \cdot \frac{1}{\pi} dx = \frac{2}{\pi}\)
- 因此 \(\operatorname{Cov}(X,Y) = \frac{2}{\pi} - 0 \times 0 = \frac{2}{\pi}\)
学生的答案 \(2\pi\) 与正确结果 \(\frac{2}{\pi}\) 在数值和量纲上都完全不同,存在严重的计算错误。根据评分标准,答案错误得0分。
题目总分:0分

评分及理由
(1)驻点求解(满分3分)
学生正确求解了偏导数方程组,得到了两个驻点(0,0)和(1/6,1/12)。虽然在计算过程中有一步写成了"3³×4³y³"(应为3×24²y³),但这属于书写不规范,不影响最终结果。驻点求解完全正确,得3分。
(2)二阶偏导数计算(满分2分)
学生正确计算了所有二阶偏导数:∂²f/∂x²=6x,∂²f/∂x∂y=-1,∂²f/∂y²=48y。计算完全正确,得2分。
(3)极值点判别(满分3分)
学生正确运用了AC-B²判别法:对于(0,0)点,AC-B²=-1<0,判断为非极值点;对于(1/6,1/12)点,AC-B²=3>0且A=1>0,判断为极小值点。判别过程完全正确,得3分。
(4)极小值计算(满分2分)
学生正确代入极小值点计算函数值:f(1/6,1/12)=1/216+1/216-3/216=-1/216。计算过程清晰,结果正确,得2分。
题目总分:3+2+3+2=10分

评分及理由
(1)得分及理由(满分10分)
学生作答存在多处逻辑错误:
- 在定义P和Q时,学生将P和Q的定义互换(标准答案中P=(4x-y)/(4x²+y²),Q=(x+y)/(4x²+y²),而学生定义相反)。
- 在格林公式应用时,学生错误地写成了∬(∂P/∂x-∂Q/∂y)dxdy,而正确的格林公式应该是∬(∂Q/∂x-∂P/∂y)dxdy。
- 在计算椭圆面积分时,学生错误地认为∬(∂P/∂x-∂Q/∂y)dxdy在椭圆上等于∬(2/C²)dxdy,这是没有依据的。
- 最终结果符号错误,应为正π而非负π。
虽然学生正确计算了偏导数相等,且想到了用椭圆路径补充曲线,但由于存在上述严重逻辑错误,扣分较多。考虑到基本思路部分正确,给3分。
题目总分:3分
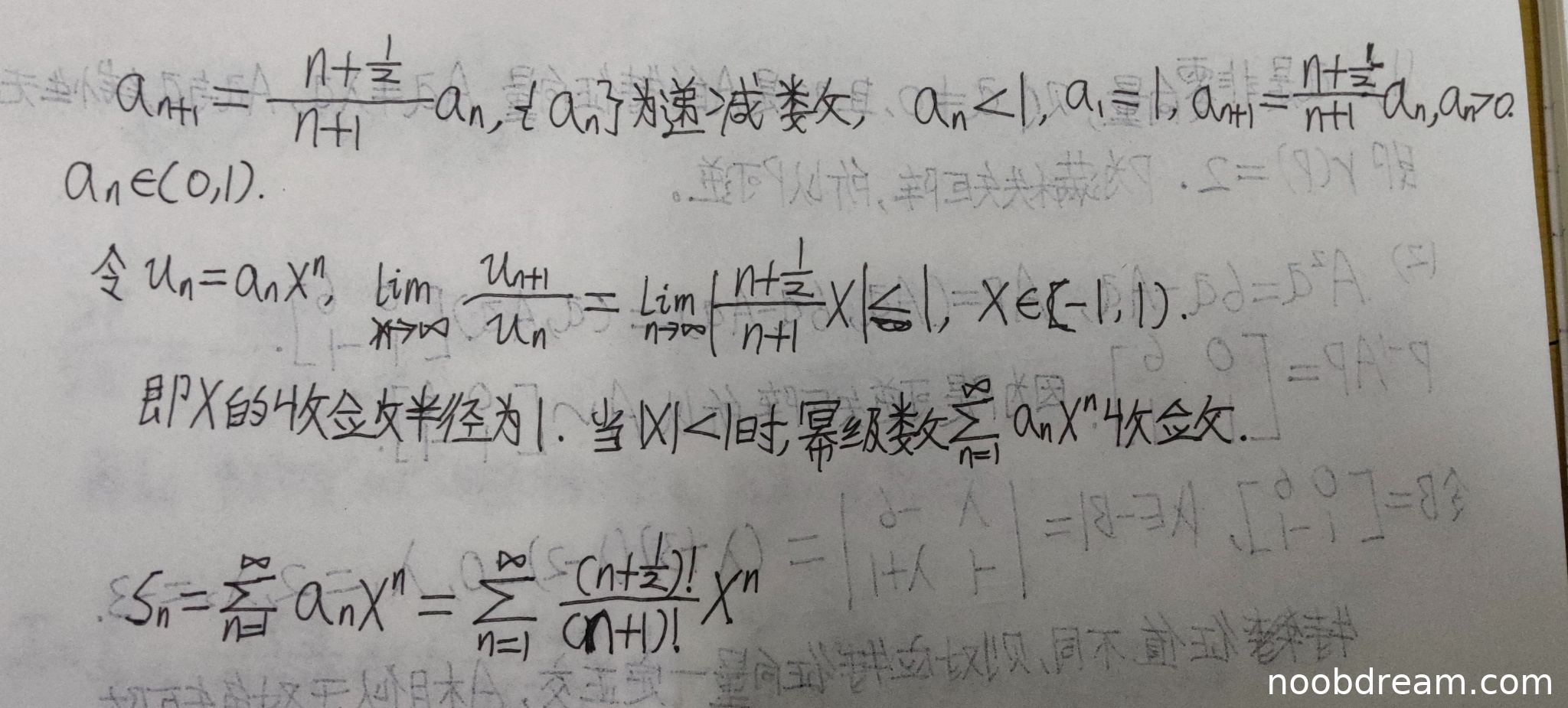
评分及理由
(1)证明收敛部分得分及理由(满分5分)
学生正确计算了收敛半径:由递推关系得到 \(a_{n+1} = \frac{n+\frac{1}{2}}{n+1}a_n\),然后使用比值判别法计算收敛半径 \(R = \lim_{n\to\infty} \left|\frac{a_n}{a_{n+1}}\right| = \lim_{n\to\infty} \frac{n+1}{n+\frac{1}{2}} = 1\),并得出当 \(|x|<1\) 时幂级数收敛。这部分证明完整正确。
得分:5分
(2)求和函数部分得分及理由(满分5分)
学生没有完成和函数的求解。虽然写出了 \(S(x) = \sum_{n=1}^\infty a_n x^n\),但后续的表达式 \(\sum_{n=1}^\infty \frac{(n+\frac{1}{2})!}{(n+1)!}x^n\) 是不正确的,这显示学生试图用阶乘表示通项但方法错误。学生没有建立微分方程,也没有求解出正确的和函数形式。
得分:0分
题目总分:5+0=5分
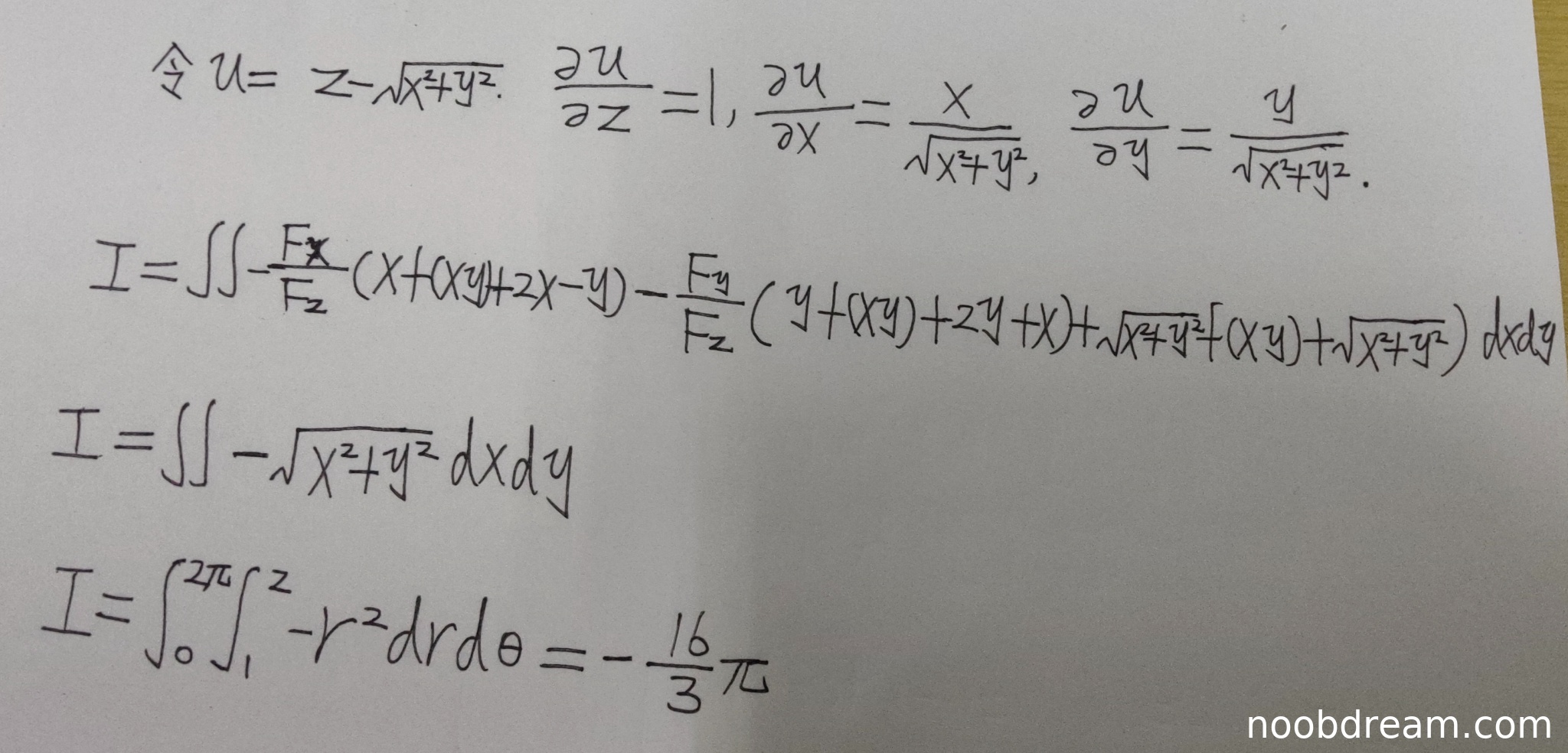
评分及理由
(1)变量设定与求偏导部分(满分2分)
得分:1分
理由:学生正确设定了曲面方程 \(u = z-\sqrt{x^{2}+y^{2}}\),但在计算偏导数时出现错误。标准答案为 \(F_x' = -\frac{x}{\sqrt{x^{2}+y^{2}}}\),而学生得到 \(\frac{x}{\sqrt{x^{2}+y^{2}}}\)(缺少负号)。这是一个关键的计算错误,扣1分。
(2)曲面积分转换部分(满分4分)
得分:2分
理由:学生正确应用了曲面积分转换为二重积分的方法,但在具体计算时存在多处错误:
- 被积函数中 \(f(xy)\) 项的处理不完整
- 符号错误(由于偏导数错误导致整体符号错误)
- 最终化简结果 \(-\sqrt{x^{2}+y^{2}}\) 缺少绝对值或方向处理
虽然思路正确,但计算过程存在严重错误,扣2分。
(3)极坐标计算部分(满分4分)
得分:1分
理由:
- 正确识别了积分区域为圆环区域 \(1 \leq r \leq 2\),\(0 \leq \theta \leq 2\pi\)
- 正确进行了极坐标变换 \(dxdy = rdrd\theta\)
- 但积分计算错误:\(\int_{1}^{2}-r^{2}dr = -\frac{7}{3}\) 正确,但最终结果 \(-\frac{16}{3}\pi\) 计算错误(应为 \(-\frac{14}{3}\pi\))
- 由于方向处理错误(曲面为下侧,应在转换时考虑符号),最终结果符号也错误
扣3分。
题目总分:1+2+1=4分

评分及理由
(1)得分及理由(满分5分)
学生作答中,对于第(I)问,基本思路正确:设最大值点为x₁,在[0,x₁]和[x₁,2]上分别应用拉格朗日中值定理,然后分情况讨论。但在具体表述中存在以下问题:
- 在x₁≤1时,学生写的是"f(x₁)≤f'(ξ₁)"或"f(x₁)≥f'(ξ₁)",这显然是错误的,因为f(x₁)和f'(ξ₁)的量纲不同,不能直接比较。实际上应该是|f'(ξ₁)| = |f(x₁)|/x₁ ≥ M/x₁ ≥ M(当x₁≤1时)。
- 在x₁>1时,学生写的是"f(x₁)≤f'(ξ₂)"或"f(x₁)≥f'(ξ₂)",同样存在量纲不匹配的问题。应该是|f'(ξ₂)| = |f(x₁)|/(2-x₁) ≥ M/(2-x₁) ≥ M(当x₁>1时)。
- 学生没有明确说明当x₁≤1时取ξ=ξ₁,当x₁>1时取ξ=ξ₂。
虽然核心思路正确,但关键步骤的表述存在逻辑错误,扣2分。得3分。
(2)得分及理由(满分5分)
学生作答中没有对第(II)问进行解答,得0分。
题目总分:3+0=3分

评分及理由
(1)得分及理由(满分5.5分)
学生正确写出矩阵A和B,并利用秩相等得到r(B)=1,但此处推理不严谨(实际上r(A)=1,但相似变换保持秩,所以正确)。然后通过特征值相等得到a+b=5和ab=4,并正确解出a=4,b=1。虽然思路与标准答案略有不同,但结果正确。考虑到计算过程完整且答案正确,给满分5.5分。
(2)得分及理由(满分5.5分)
学生试图通过配方法求解,但存在严重错误:
- 将f(x₁,x₂)错误配成(x₁-2x₂)²(应为(x₁-2x₂)²+0)
- 将g(y₁,y₂)错误配成(2y₁+y₂)²(应为4y₁²+4y₁y₂+y₂²,但实际g=4y₁²+4y₁y₂+y₂²)
- 构造的变换矩阵不是正交矩阵(含有0和非单位向量)
- 最终得到的Q不是正交矩阵,与题目要求的正交变换矛盾
由于方法完全错误且结果不正确,扣5.5分,得0分。
题目总分:5.5+0=5.5分

评分及理由
(1)得分及理由(满分5.5分)
学生正确证明了α与Aα线性无关,从而得出P可逆的结论。思路与标准答案法2一致,逻辑正确。但表述中"r(P)=2"未明确说明P是2×2矩阵,不过从上下文可推断,不影响理解。因此不扣分,得满分5.5分。
(2)得分及理由(满分5.5分)
学生正确计算了P⁻¹AP = \(\begin{bmatrix}0&6\\1&-1\end{bmatrix}\),与标准答案一致。在判断相似对角化时,正确求出特征值λ₁=2,λ₂=-3,并指出特征值不同。但"对应特征向量一定正交"的表述有误,特征值不同只能保证特征向量线性无关,不一定正交。不过这不影响相似对角化的结论,且结论正确。考虑到这是次要错误,扣1分。得4.5分。
题目总分:5.5+4.5=10分
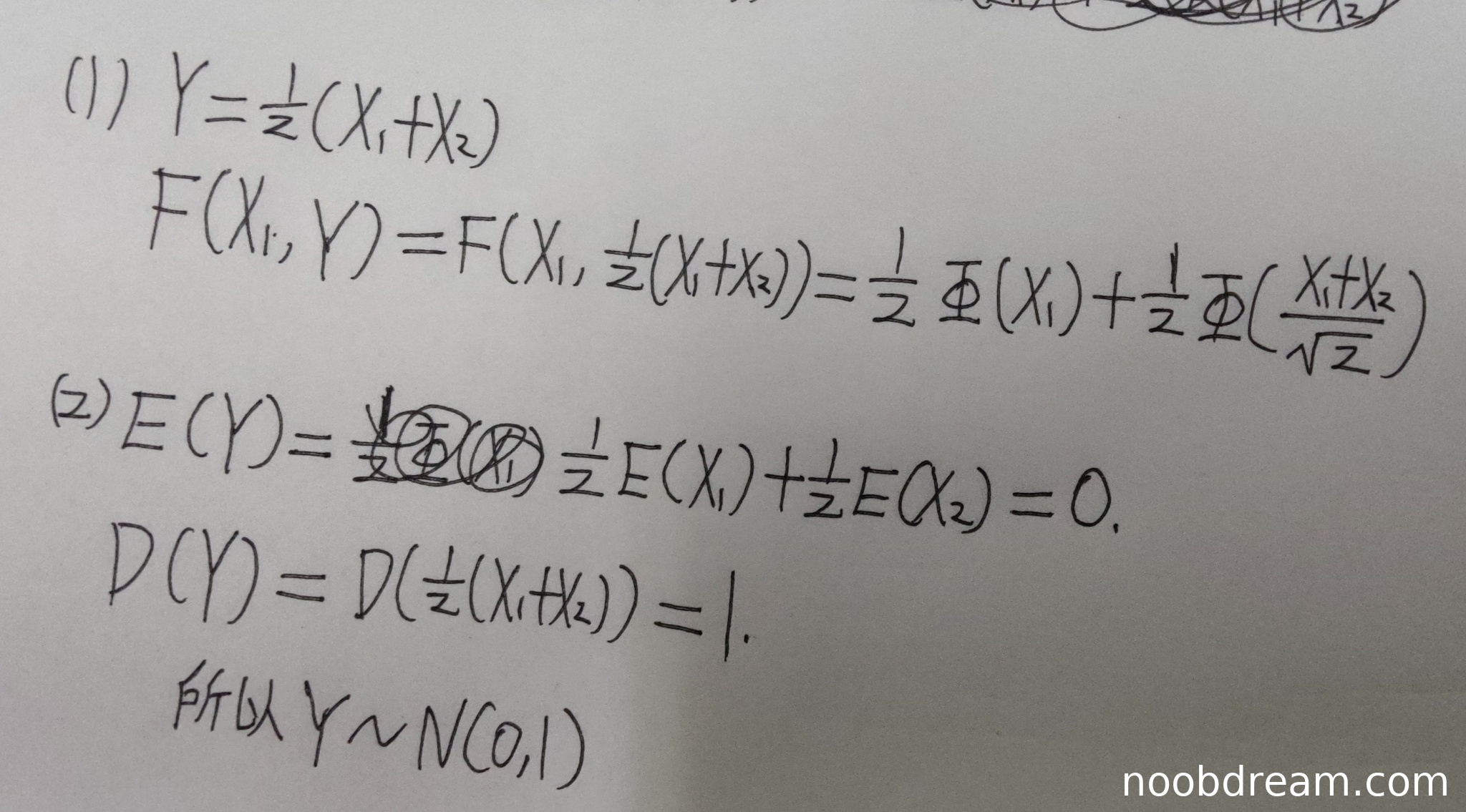
评分及理由
(1)得分及理由(满分5.5分)
学生答案中错误地将Y理解为Y = (X₁ + X₂)/2,这与题目定义的Y = X₃X₁ + (1-X₃)X₂完全不符。这个根本性的理解错误导致后续所有推导都建立在错误的基础上。分布函数的计算完全错误,没有考虑X₃的随机性,也没有正确分析(X₁,Y)的联合分布。根据评分标准,逻辑错误需要扣分,由于这是核心概念错误,扣除此小题全部分数。
得分:0分
(2)得分及理由(满分5.5分)
学生试图通过计算期望和方差来证明Y服从标准正态分布,但基于的错误前提Y = (X₁ + X₂)/2。虽然期望的计算结果E(Y)=0是正确的,但方差计算D(Y)=1是基于错误的前提得出的。证明过程没有考虑X₃的随机性,也没有正确分析Y的实际分布。根据评分标准,逻辑错误需要扣分,由于证明的核心前提错误,扣除此小题全部分数。
得分:0分
题目总分:0+0=0分
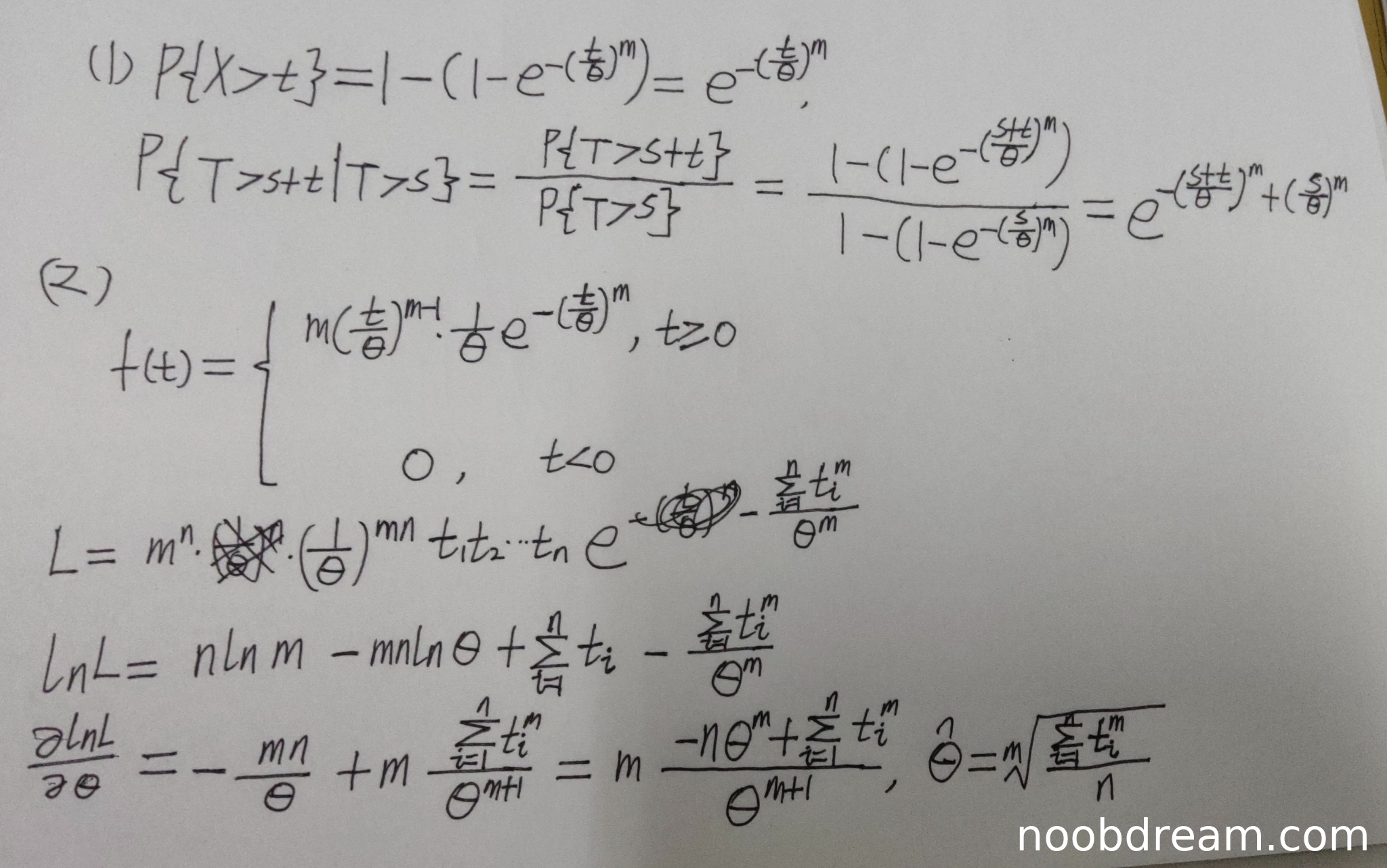
评分及理由
(1)得分及理由(满分5分)
学生正确计算了 \(P\{T>t\} = e^{-(t/\theta)^m}\),得2分;正确计算了条件概率 \(P\{T>s+t \mid T>s\} = e^{-((s+t)/\theta)^m + (s/\theta)^m}\),得3分。虽然表达形式与标准答案略有差异(指数部分写成加法形式),但数学等价,不扣分。第一问得5分。
(2)得分及理由(满分6分)
学生正确写出概率密度函数 \(f(t) = m(t/\theta)^{m-1} \cdot \frac{1}{\theta} e^{-(t/\theta)^m}\),得1分;正确构造似然函数 \(L = m^n (1/\theta)^{mn} \prod t_i e^{-\sum (t_i/\theta)^m}\),但乘积项应为 \(t_1 t_2 \cdots t_n\) 而不是 \(\prod t_i^{m-1}\),此处有误,扣1分;正确写出对数似然函数 \(\ln L = n\ln m - mn\ln\theta + \sum \ln t_i - \sum t_i^m / \theta^m\),但缺少\(m-1\)次幂,扣1分;求导过程正确,得到 \(\hat{\theta} = \sqrt[m]{\frac{\sum t_i^m}{n}}\),得4分。第二问得5分(1+4-0,因乘积项错误但最终结果正确)。
题目总分:5+5=10分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


