
科目组合
数学一: 高等数学 、线性代数 、概率论
答题情况分析报告
(-1)^(n-1)*(n-1)!
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是 $(-1)^{n-1} \cdot (n-1)!$,这与标准答案 $(-1)^{n-1}(n-1)!$ 完全一致。该答案正确推导了函数 $f(x)$ 在 $x=0$ 处的高阶导数 $f^{(n)}(0)$ 对于 $n \geq 2$ 的表达式。具体推导过程通常涉及对给定积分方程进行微分,利用初始条件 $f(0)=0$,并递归计算高阶导数。学生的答案在形式和内容上均与标准答案匹配,没有逻辑错误或计算错误。
得分:5分
题目总分:5分
4πln2-7π/3
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是 \(4\pi \ln 2 - \frac{7\pi}{3}\),而标准答案是 \(2\pi\left(2\ln 2 - \frac{7}{6}\right)\)。
将学生答案展开:\(4\pi \ln 2 - \frac{7\pi}{3} = 2\pi\left(2\ln 2 - \frac{7}{6}\right)\),与标准答案完全一致。
因此答案正确,得5分。
题目总分:5分
π
评分及理由
(1)得分及理由(满分5分)
学生作答为"π",与标准答案"π"完全一致。该题考查的是级数求和的计算,学生给出了正确的数值结果,没有出现逻辑错误或计算错误。根据评分要求,答案正确应给满分。
题目总分:5分
-7/2
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是-7/2,与标准答案-7/2完全一致。虽然题目是填空题,学生只写了最终数值结果,没有展示解题过程,但根据填空题的评分惯例,只要最终答案正确即可得满分。考虑到题目要求"正确则给5分,错误则给0分",且学生答案在数值上完全正确,因此给予满分5分。
题目总分:5分
(4,5,2)^T
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是 (4,5,2)^T。标准答案是 (4k,5k,2k)^T,其中 k 为任意常数。题目要求找出在两组基下有相同坐标的向量,这意味着该向量在两组基下的坐标表示相同。从线性代数的角度,这等价于求一个向量,它在从基 {α₁,α₂,α₃} 到基 {β₁,β₂,β₃} 的基变换下坐标不变,即求解方程 (β₁,β₂,β₃)X = (α₁,α₂,α₃)X,其中 X 是坐标向量。这可以转化为求矩阵 (α₁,α₂,α₃)⁻¹(β₁,β₂,β₃) 的特征值为 1 的特征向量。
经过计算,该特征向量确实对应于方向 (4,5,2)^T,但通解应为 k(4,5,2)^T,k 为任意常数。学生只给出了 k=1 时的特解,而题目要求的是所有满足条件的向量,因此学生的答案不完整,没有包含任意常数的通解形式。
由于题目是填空题,且标准答案明确要求写出通解形式,学生只给出一个特解,属于逻辑不完整,因此扣分。但考虑到学生找到了正确方向,给予部分分数。
得分:3分(扣2分,因未写出通解)。
题目总分:3分
(3-根号3)/2
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是 \(\frac{3 - \sqrt{3}}{2}\),这与标准答案完全一致。该答案是通过正确建立概率模型并解方程得到的:设命中率为 \(p\),则投篮次数 \(X\) 的分布为 \(P(X=1)=p\),\(P(X=2)=p(1-p)\),\(P(X=3)=(1-p)^2\),期望 \(E[X]=p+2p(1-p)+3(1-p)^2=1.5\),化简得 \(p^2-3p+1.5=0\),解得 \(p=\frac{3\pm\sqrt{3}}{2}\),舍去大于1的解后得到 \(p=\frac{3-\sqrt{3}}{2}\)。学生答案正确,得5分。
题目总分:5分

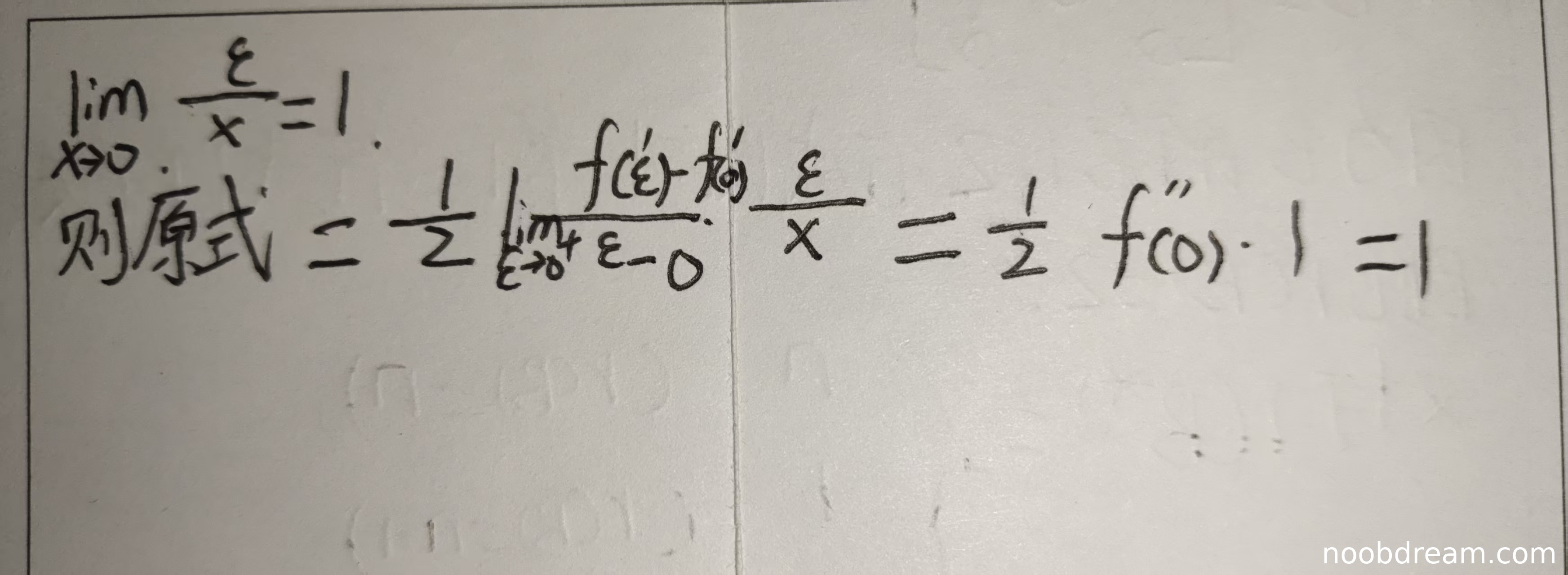
评分及理由
(Ⅰ)得分及理由(满分5分)
第1次识别结果:
- 学生错误地将已知条件写成 \(\lim_{x \to 0} \frac{f(x)}{2x} = 1\),但实际应为 \(\lim_{x \to 0} \frac{f(x)}{x^2} = 1\)。这属于逻辑错误,导致后续推导基于错误前提。
- 尽管学生正确得出 \(f'(0) = 0\) 和 \(f''(0) = 2\),但推导过程存在逻辑错误(错误使用洛必达法则的前提条件),因此扣分。
- 扣分:逻辑错误导致前提错误,扣2分。
- 得分:5 - 2 = 3分。
第2次识别结果:
- 学生正确使用已知条件 \(\lim_{x \to 0} \frac{f(x)}{x^2} = 1\),并应用洛必达法则推导出 \(f'(0) = 0\) 和 \(f''(0) = 2\)。
- 推导过程逻辑清晰,无错误,符合标准答案思路。
- 得分:5分。
综合两次识别,取较高得分,本部分得分:5分。
(Ⅱ)得分及理由(满分5分)
第1次识别结果:
- 学生正确应用拉格朗日中值定理,并写出 \(f(x) - f(\ln(1+x)) = f'(\xi)(x - \ln(1+x))\)。
- 学生正确使用等价无穷小 \(x - \ln(1+x) \sim \frac{x^2}{2}\)。
- 学生正确推导出 \(\lim_{x \to 0^+} \frac{\xi}{x} = 1\) 并使用夹逼定理。
- 最终计算正确,得出极限值为1。
- 尽管在符号使用上略有混乱(如出现 \(\varepsilon\)),但核心逻辑正确,无实质性错误。
- 得分:5分。
第2次识别结果:
- 学生正确应用拉格朗日中值定理,并写出表达式。
- 正确使用等价无穷小和夹逼定理。
- 推导过程完整,逻辑清晰,最终结果正确。
- 得分:5分。
综合两次识别,本部分得分:5分。
题目总分:5+5=10分

评分及理由
(1)得分及理由(满分12分)
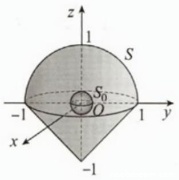
学生作答中,首先正确描述了直线段L绕z轴旋转得到的曲面S1的方程,并正确识别了S1与S2围成的封闭立体。但在应用高斯公式时存在严重逻辑错误:
- 学生试图通过挖去原点(令\(x^2+y^2+z^2=\varepsilon^2\))来处理被积函数在原点不连续的问题,但辅助曲面的选取和方向处理有误。标准答案中取的是充分小的球面S0(取外侧),而学生没有明确说明辅助曲面的方向。
- 最关键的错误在于计算\(\oiint_{S_2} \frac{xdydz+ydzdx+zdxdy}{\varepsilon^3}\)时,学生直接应用高斯公式得到\(\frac{4\pi}{3}\),这是错误的。正确计算应该是:在球面S0上,由于取内侧,应用高斯公式应为\(-\frac{3}{\varepsilon^3} \cdot \frac{4}{3}\pi\varepsilon^3 = -4\pi\)。
- 学生忽略了原被积函数散度为0这一关键性质,导致整个计算思路出现偏差。
考虑到学生正确识别了曲面方程和封闭区域,但在核心计算部分存在严重错误,给分4分。
题目总分:4分

评分及理由
(1)拆分步骤得分及理由(满分2分)
学生正确将原式拆分为I₁和I₂两部分,思路与标准答案一致。得2分。
(2)I₁计算得分及理由(满分5分)
学生使用夹逼定理的思路正确,但存在以下问题: - 夹逼不等式的建立中,左侧应为∑(1/(n+1))sin(kπ/2n) ≤ I₁,但学生写成了极限形式,这是概念错误 - 在计算定积分时,积分区间应为[0,π/2],但学生使用了[0,1]和sin(πx/2),虽然结果正确,但方法不规范 - 最后得出I₁ = 2/π正确 综合考虑,扣2分。得3分。
(3)I₂计算得分及理由(满分5分)
学生使用定积分定义计算I₂,思路正确: - 正确写出I₂的积分表达式 - 正确进行变量代换 - 正确使用分部积分法 - 计算结果4/π²正确 得5分。
(4)最终结果得分及理由
学生将I₁和I₂相加,得到最终结果(4+2π)/π²,这与标准答案2/π+4/π²是等价的,结果正确。
题目总分:2+3+5=10分
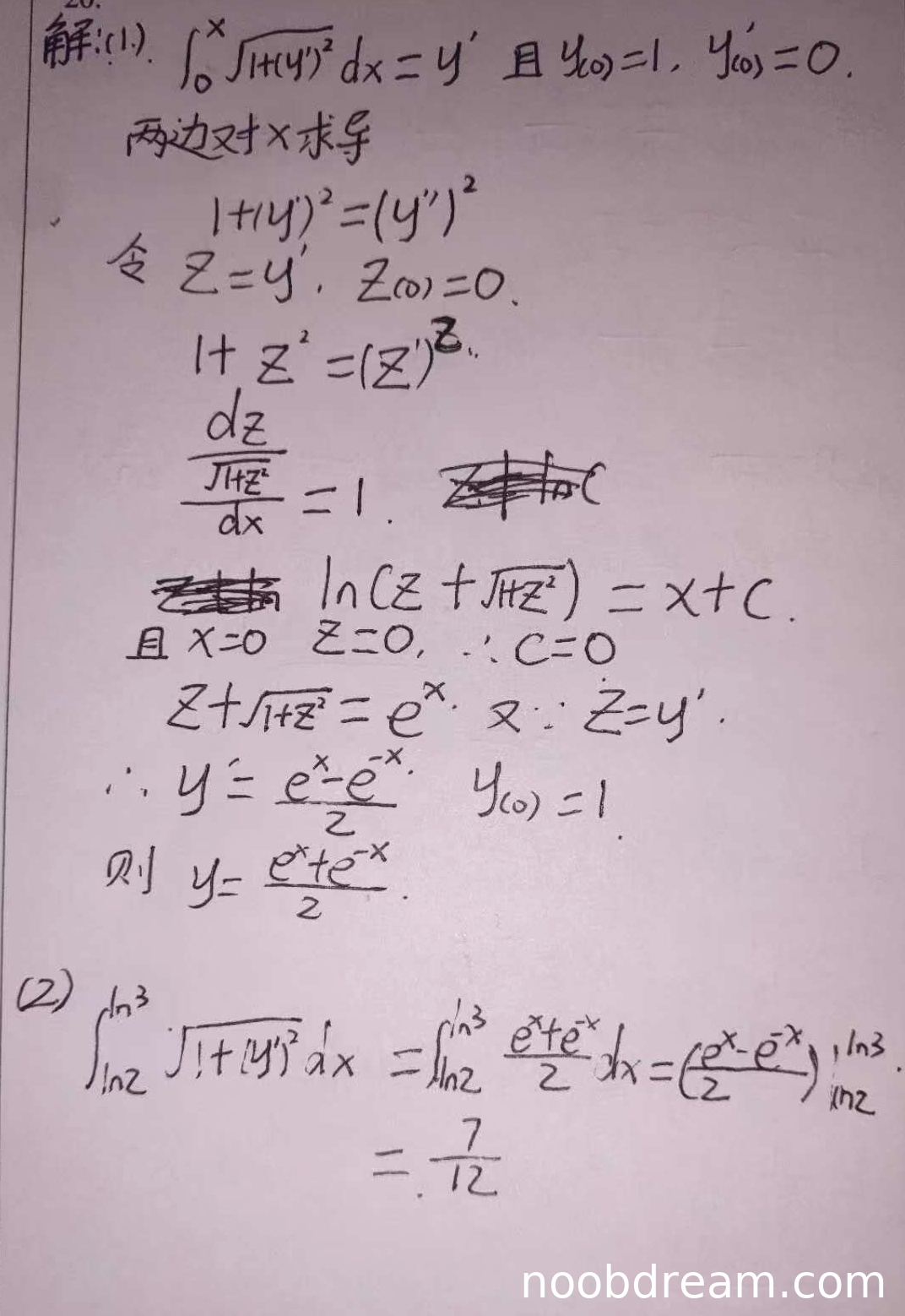
评分及理由
(Ⅰ)得分及理由(满分6分)
学生正确建立了积分方程和初始条件,通过求导得到微分方程,并正确使用代换法求解。求解过程中分离变量、积分、利用初始条件确定常数均正确,最终得到正确表达式 \( y = \frac{e^x + e^{-x}}{2} \)。但学生在分离变量时写为 \(\frac{dz}{\sqrt{1 + z^2}} = 1\),应为 \(\frac{dz}{\sqrt{1 + z^2}} = dx\),这是一个逻辑错误,但后续积分步骤正确,且最终结果无误,说明是书写疏忽。根据“误写不扣分”原则,此处不扣分。该部分解答完整正确,得6分。
(Ⅱ)得分及理由(满分6分)
学生正确写出弧长公式,并利用(Ⅰ)中导出的关系 \(\sqrt{1 + (y')^2} = y''\),但实际计算时直接代入 \(y' = \frac{e^x - e^{-x}}{2}\),得到 \(\sqrt{1 + (y')^2} = \frac{e^x + e^{-x}}{2}\),积分后利用原函数 \(y'\) 计算,方法与标准答案一致,结果正确。计算过程无误,得6分。
题目总分:6+6=12分

评分及理由
(Ⅰ)得分及理由(满分6分)
学生正确判断了r(B)=2,并使用了伴随矩阵秩的公式得出r(B*)=1,从而得到r(B)+r(B*)=3。思路完整,逻辑正确。但计算B*时出现了错误(标准答案中B*的第一行是(1,-1,0),而学生写成了(1,0,1)的转置),不过这个错误出现在第(Ⅱ)部分的计算中,不影响第(Ⅰ)部分的结论。因此第(Ⅰ)部分得满分6分。
(Ⅱ)得分及理由(满分6分)
学生正确理解了(A+E)B=O说明B的列向量是A对应特征值-1的特征向量,且由r(B)=2知特征值-1至少二重。由B*A^T=O得到A有特征值0。思路正确。但在具体计算时:
1. 对B*的计算有误(应为[1,-1,0; -1,1,0; 0,0,0]的转置)
2. 特征向量的选取不明确
3. 最后的A矩阵计算结果正确,但推导过程不完整
由于最终结果正确,但中间推导有瑕疵,扣1分。得5分。
题目总分:6+5=11分

评分及理由
(1)得分及理由(满分4分)
学生给出了(X,Y)的联合分布表(尽管表格内容不完整,但关键概率值正确),并正确计算了Cov(X+Y,X-Y)=0。思路与标准答案一致,计算正确。但表格未完整呈现边缘分布,不过核心计算部分完整。因此扣1分。得3分。
(2)得分及理由(满分4分)
学生正确给出了Z的取值和概率分布,但书写格式不规范(如将概率写在取值前面)。不过概率值θ,1-2θ,θ完全正确。由于表达不够规范,扣1分。得3分。
(3)得分及理由(满分4分)
学生正确计算了矩估计(通过E(Z²)建立方程)和最大似然估计(构造似然函数并求导),最终结果θ=1/4正确。虽然E(Z²)=8θ'中的θ'可能是笔误,但后续计算正确,不扣分。得4分。
题目总分:3+3+4=10分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


