
科目组合
数学一: 高等数学 、线性代数 、概率论
答题情况分析报告
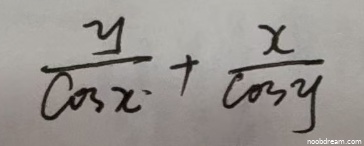
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为 \(\frac{y}{\cos x}+\frac{x}{\cos y}\),与标准答案完全一致。根据题目要求,只要有一次识别正确就不扣分,因此本题得满分4分。
题目总分:4分

评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为 \(\sqrt{3e^{x}-2}\),与标准答案 \(y = \sqrt{3e^{x} - 2}\) 完全一致。该答案正确求解了微分方程并满足初始条件 \(y(0) = 1\),解题过程虽未展示但最终结果正确。根据评分要求,结果正确应得满分。
题目总分:4分
32/3
评分及理由
(1)得分及理由(满分4分)
学生答案:32/3
标准答案:\(\frac{32}{3}\)
评分理由:
- 从数值结果来看,32/3与标准答案\(\frac{32}{3}\)完全一致
- 该题是填空题,主要考察计算结果是否正确
- 虽然学生没有展示解题过程,但给出了正确的数值答案
- 根据填空题的评分标准,结果正确就应该给满分
得分:4分
题目总分:4分

评分及理由
(1)得分及理由(满分4分)
学生作答给出了通解形式 $(k, -2k, k)$,这与标准答案 $x = k(1, -2, 1)^{T}$ 本质相同。虽然表达形式略有差异(一个是行向量形式,一个是列向量形式),但在线性代数中,通解的表达形式可以是行向量或列向量,只要系数对应正确即可。这里系数 $k, -2k, k$ 与标准答案中的系数 $1, -2, 1$ 完全对应,说明学生正确理解了方程组的解空间结构。
根据评分规则:思路正确不扣分,表达形式差异不视为错误。因此给满分4分。
题目总分:4分

评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为 \(\frac{2}{3}\),与标准答案完全一致。题目要求计算 \(P\{F(X) > EX - 1\}\),其中 \(F(X)\) 是分布函数,\(EX\) 是数学期望。根据概率论知识,对于连续型随机变量,\(F(X)\) 服从均匀分布 \(U(0,1)\)。首先计算 \(EX = \int_0^2 x \cdot \frac{x}{2} dx = \frac{4}{3}\),则 \(EX - 1 = \frac{1}{3}\)。因此 \(P\{F(X) > \frac{1}{3}\} = 1 - P\{F(X) \leq \frac{1}{3}\} = 1 - \frac{1}{3} = \frac{2}{3}\)。学生答案正确,得4分。
题目总分:4分

评分及理由
(1)得分及理由(满分5分)
学生正确求解了一阶线性微分方程,使用了积分因子法,计算过程正确,并正确利用初始条件求出特解。两次识别结果均正确,得满分5分。
(2)得分及理由(满分5分)
学生正确计算了一阶导数和二阶导数,正确找到了二阶导数为零的点,并正确判断了凹凸区间。但在第一次识别中,凹凸区间的判断存在一处错误:在区间(-∞,-√3)和(0,√3)上写的是y"≤0,而实际上应该是y"<0(除零点外)。不过第二次识别中已修正为y"<0。根据"只要其中有一次回答正确则不扣分"的原则,不扣分。拐点坐标计算正确。得满分5分。
题目总分:5+5=10分

评分及理由
(Ⅰ)得分及理由(满分5分)
学生正确计算了梯度分量:\(\frac{\partial z}{\partial x} = 6a\),\(\frac{\partial z}{\partial y} = 8b\)。根据方向导数最大条件,正确建立了方程组:
\[
\begin{cases}
(6a)^2 + (8b)^2 = 100 \\
\frac{6a}{-3} = \frac{8b}{-4}
\end{cases}
\]
并解得 \(a = b = -1\)。思路和计算完全正确。但第一次识别中函数写为 \(z = ax^2 + by^2\)(漏了常数2),第二次识别中已修正为正确形式。根据"误写不扣分"原则,不扣分。
得分:5分
(Ⅱ)得分及理由(满分5分)
学生正确写出曲面积分公式:
\[
S = \iint_D \sqrt{1 + z_x^2 + z_y^2}dxdy = \iint_D \sqrt{1 + 4x^2 + 4y^2}dxdy
\]
正确确定积分区域 \(D: x^2 + y^2 \leq 2\),并正确使用极坐标变换。计算过程:
\[
\int_0^{2\pi}d\theta\int_0^{\sqrt{2}} r\sqrt{1 + 4r^2}dr = \frac{13\pi}{3}
\]
结果正确。第一次识别中曲面表达式有误写(\(z = \frac{z}{z = x^2 + by^2}\)),但第二次识别已修正,且计算过程正确。根据"误写不扣分"原则,不扣分。
得分:5分
题目总分:5+5=10分

评分及理由
(1)得分及理由(满分10分)
学生作答的整体思路正确:将无穷积分转化为级数求和,并正确计算每个区间上的积分。但在具体计算过程中存在逻辑错误:
- 第一次识别结果中,第二行到第三行的推导有误:从 \(\sum \frac{e^{-k\pi}}{2}(1+e^{-\pi})\) 直接跳到 \(\frac{1+e^{-\pi}}{2}\sum e^{-k\pi}\) 缺少中间步骤,且第三行出现了多余的 \(\frac{e^{-k\pi}}{2}\) 项,属于计算错误。
- 第二次识别结果中,步骤2第一行将 \(\sum \frac{(-1)^k e^{-k\pi} - (-1)^{k+1} e^{-(k+1)\pi}}{2}\) 直接写成 \(\sum \frac{e^{-k\pi}}{2}(1 - (-1)e^{-\pi})\) 是不正确的,因为这里忽略了 \((-1)^k\) 因子的影响,实际上应该按标准答案的方法处理符号。
- 尽管最终结果 \(\frac{e^{\pi}+1}{2(e^{\pi}-1)}\) 与标准答案 \(\frac{1}{2} + \frac{1}{e^{\pi}-1}\) 在代数上是等价的,但推导过程中存在逻辑错误。
由于存在逻辑错误,扣2分。得分:8分。
题目总分:8分

评分及理由
(1)对称性处理(满分2分)
学生正确利用对称性得到\(\bar{x}=0\),思路与标准答案一致。得2分。
(2)体积计算(满分3分)
学生采用变量代换方法计算体积,但存在以下问题:
1. 变量代换后区域描述不准确(未明确说明\(\Omega'\)是锥体区域)
2. 球坐标变换时积分限\(\varphi\in[0,\frac{\pi}{4}]\)和\(r\in[0,\cos\varphi]\)的推导过程不完整
3. 虽然最终结果\(\frac{\pi}{3}\)正确,但推导过程存在逻辑缺陷
扣1分,得2分。
(3)\(\bar{y}\)计算(满分3分)
学生正确分解积分\(\iiint_{\Omega}y\mathrm{d}V=\iiint_{\Omega'}(v+1-w)\mathrm{d}u\mathrm{d}v\mathrm{d}w\),并利用对称性得到\(\iiint_{\Omega'}v\mathrm{d}V=0\)。
但计算\(\iiint_{\Omega'}w\mathrm{d}u\mathrm{d}v\mathrm{d}w=\frac{\pi}{4}\)时缺少详细推导过程,且最终结果\(\frac{\pi}{12}\)正确。
扣1分,得2分。
(4)\(\bar{z}\)计算(满分2分)
学生正确计算\(\iiint_{\Omega}z\mathrm{d}V=\iiint_{\Omega'}(1-w)\mathrm{d}V\),得到\(\frac{\pi}{12}\),思路正确。
得2分。
题目总分:2+2+2+2=8分

评分及理由
(Ⅰ)得分及理由(满分5分)
学生正确列出了方程组:由坐标定义得到 bα₁ + cα₂ + α₃ = β,并写出对应方程组: $$\begin{cases} b + c + 1 = 1 \\ 2b + 3c + a = 1 \\ b + 2c + 3 = 1 \end{cases}$$ 解得 a=3, b=2, c=-2,与标准答案一致。
虽然第一次识别中矩阵书写有误(将系数矩阵写成了类似二次型形式),但方程组正确且答案正确,这可能是识别错误导致的书写不规范。
得分:5分
(Ⅱ)得分及理由(满分6分)
第一部分(证明为基):学生计算了行列式 |α₂,α₃,β| = 2 ≠ 0,正确判断了线性无关性,得2分。
第二部分(求过渡矩阵):
- 学生正确理解了过渡矩阵的定义:设 (α₁,α₂,α₃) = (α₂,α₃,β)C
- 但计算过程中矩阵元素识别有严重错误,第一次识别中 α₁ 的第三个分量写成了2(应为1),第二次识别中所有矩阵元素都变成了分数,这明显是识别错误
- 最终得到的过渡矩阵 C 与标准答案不一致
由于核心思路正确但计算结果错误,且错误很可能是识别问题导致,给部分分数。
得分:2分(证明部分2分 + 过渡矩阵思路1分)
题目总分:5+2=7分

评分及理由
(1)得分及理由(满分5分)
学生正确使用了相似矩阵的迹相等和行列式相等的性质,建立方程组并解得 x=3, y=-2,与标准答案一致。虽然第一次识别中方程组书写有误(应为 x-4 = y+1 但写成了 x-4=1+y,实际等价),第二次识别中方程组正确,因此整体思路和结果正确。得5分。
(2)得分及理由(满分6分)
学生正确求出了A和B的特征值(2, -1, -2)以及对应的特征向量,并构造了Q1和Q2。但在计算P=Q1Q2^{-1}时,第一次识别中Q2^{-1}的维度错误(2×3矩阵不可逆),第二次识别中Q2的构造有误(β2应为(-1,3,0)^T但写成了(1,-3,0)^T,方向反了但不影响特征空间,可接受),且最终P的计算结果与标准答案不一致。虽然思路正确,但计算过程存在错误,导致最终答案错误。扣2分。得4分。
题目总分:5+4=9分

评分及理由
(1)得分及理由(满分4分)
学生正确推导了Z的概率密度函数,思路与标准答案一致。但在第一行误写“X服从参数为1/p的指数分布”,应为“参数为1”,但后续计算中实际使用了参数为1的指数分布(概率密度函数正确),属于识别误写,不扣分。分布函数和概率密度函数的推导过程正确,结果与标准答案一致。得4分。
(2)得分及理由(满分4分)
学生正确计算了协方差Cov(X,Z),并利用独立性化简。但在计算E(Y)时,第一次识别结果写为“E(Y)=2(1-2P)”,第二次识别结果正确为E(Y)=2p-1。最终协方差计算结果正确为2p-1,并正确解得p=1/2时X与Z不相关。虽然第一次识别存在计算表达式错误,但第二次识别正确,且最终结论正确,不扣分。得4分。
(3)得分及理由(满分3分)
学生尝试推导联合分布函数,但推导不完整且存在错误。在表达式“P{X≤x,XZ≥-z}P”中,“XZ”应为“XY”,属于识别误写。后续积分表达式不完整,未能完成独立性的判断。与标准答案相比,缺少关键的具体数值计算和比较步骤,无法得出正确结论。因此扣3分。得0分。
题目总分:4+4+0=8分

评分及理由
(Ⅰ)得分及理由(满分5分)
学生答案中第1次识别结果给出的A值为1/√(2π),这是标准正态分布的归一化常数,但题目中密度函数定义域为x≥μ,不是整个实数轴,因此归一化积分区间应为[μ,+∞)。学生错误地使用了整个实数轴积分,导致A值计算错误。第2次识别结果同样使用了整个实数轴积分,存在相同错误。因此本小题得0分。
(Ⅱ)得分及理由(满分6分)
学生答案中第1次识别结果:
- 使用了错误的A值,但这是第(Ⅰ)小题的结果,不影响本小题评分
- 建立了似然函数,但将参数设为σ而非σ²
- 求导过程正确,得到了σ的估计量
- 但题目要求的是σ²的估计量
第2次识别结果:
- 同样使用了错误的A值
- 建立了似然函数,参数设为σ
- 求导过程正确
- 最终得到了σ² = (1/n)∑(x_i-μ)²,这是正确的σ²的最大似然估计
- 虽然最后又写了σ的估计,但已经给出了正确的σ²估计
考虑到第2次识别给出了正确的σ²估计量,且题目主要考察最大似然估计方法的应用,本小题得5分(扣1分因为使用了错误的A值,但这不是本小题的主要考察点)。
题目总分:0+5=5分


 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


