
科目组合
数学一: 高等数学 、线性代数 、概率论
答题情况分析报告
评分及理由
(1)得分及理由(满分4分)
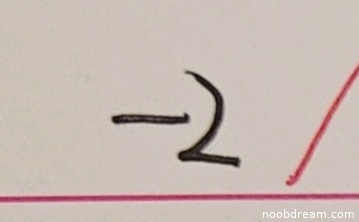
学生作答为"-2",与标准答案一致。该题考察极限计算,核心思路是利用重要极限公式。学生答案正确,说明掌握了相关知识点。根据评分标准,答案正确给满分4分。
题目总分:4分
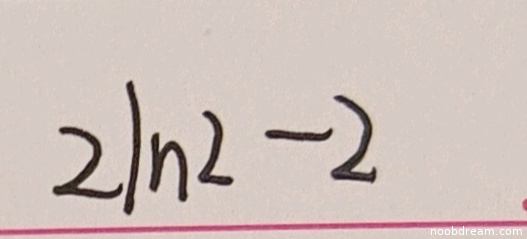
评分及理由
(1)得分及理由(满分4分)
学生答案为“2ln2 - 2”,与标准答案“2(ln2 - 1)”等价。因为“2(ln2 - 1)”展开后即为“2ln2 - 2”。答案完全正确,没有逻辑错误或计算错误。
题目总分:4分
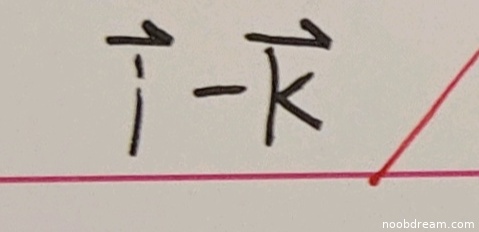
评分及理由
(1)得分及理由(满分4分)
学生作答结果为:\(\overrightarrow{i}-\overrightarrow{k}\)。该题要求计算向量场\(\boldsymbol{F}(x,y,z) = xy\boldsymbol{i} - yz\boldsymbol{j} + zx\boldsymbol{k}\)在点\((1,1,0)\)处的旋度\(\text{rot}\ \boldsymbol{F}\)。
旋度的计算公式为: \[ \text{rot}\ \boldsymbol{F} = \nabla \times \boldsymbol{F} = \begin{vmatrix} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{vmatrix} \] 其中\(\boldsymbol{F} = P\boldsymbol{i} + Q\boldsymbol{j} + R\boldsymbol{k}\),即\(P = xy, Q = -yz, R = zx\)。
计算得: \[ \text{rot}\ \boldsymbol{F} = \left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right)\boldsymbol{i} - \left( \frac{\partial R}{\partial x} - \frac{\partial P}{\partial z} \right)\boldsymbol{j} + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right)\boldsymbol{k} \] 代入函数: \[ \frac{\partial R}{\partial y} = \frac{\partial (zx)}{\partial y} = 0, \quad \frac{\partial Q}{\partial z} = \frac{\partial (-yz)}{\partial z} = -y \] \[ \frac{\partial R}{\partial x} = \frac{\partial (zx)}{\partial x} = z, \quad \frac{\partial P}{\partial z} = \frac{\partial (xy)}{\partial z} = 0 \] \[ \frac{\partial Q}{\partial x} = \frac{\partial (-yz)}{\partial x} = 0, \quad \frac{\partial P}{\partial y} = \frac{\partial (xy)}{\partial y} = x \] 因此: \[ \text{rot}\ \boldsymbol{F} = (0 - (-y))\boldsymbol{i} - (z - 0)\boldsymbol{j} + (0 - x)\boldsymbol{k} = y\boldsymbol{i} - z\boldsymbol{j} - x\boldsymbol{k} \] 在点\((1,1,0)\)处: \[ \text{rot}\ \boldsymbol{F}(1,1,0) = 1\cdot\boldsymbol{i} - 0\cdot\boldsymbol{j} - 1\cdot\boldsymbol{k} = \boldsymbol{i} - \boldsymbol{k} \]
标准答案为\(\boldsymbol{i} - \boldsymbol{k}\),学生作答\(\overrightarrow{i}-\overrightarrow{k}\)与标准答案一致。虽然学生使用了\(\overrightarrow{i}\)和\(\overrightarrow{k}\)的写法(可能表示向量),但根据题目中向量符号的使用习惯(\(\boldsymbol{i}, \boldsymbol{k}\)),这属于符号表示的微小差异,且核心逻辑和计算结果完全正确。根据评分规则,思路正确且答案正确,不扣分。
得分:4分
题目总分:4分

评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为 \(-\frac{\pi}{3}\),与标准答案完全一致。该题是填空题,主要考察对曲线积分的计算能力,答案正确即表明解题过程和结果均符合要求。根据评分规则,答案正确给满分4分。
题目总分:4分

评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为"-1",与标准答案完全一致。题目要求计算二阶矩阵A的行列式|A|,已知条件表明A有两个不同的特征值,且存在线性无关的特征向量α₁, α₂满足A²(α₁+α₂) = α₁+α₂。根据特征值性质,若λ是A的特征值,则λ²是A²的特征值。由A²(α₁+α₂) = α₁+α₂可知1是A²的特征值,对应的特征向量为α₁+α₂。由于α₁, α₂对应A的不同特征值λ₁, λ₂,且A²的特征值为λ₁², λ₂²,因此1必须是某个λᵢ²。又因为α₁+α₂不是A的特征向量(否则α₁, α₂线性相关),所以1不能同时是λ₁²和λ₂²,于是{λ₁², λ₂²} = {1, μ}且μ ≠ 1。由特征值性质,|A| = λ₁λ₂,且|A²| = (λ₁λ₂)² = |A|²。同时A²的特征值之积为1×μ = μ,所以|A|² = μ。另外,A²有特征值1对应特征向量α₁+α₂,考虑A²在基{α₁, α₂}下的矩阵为diag(λ₁², λ₂²),计算A²(α₁+α₂) = (λ₁², λ₂²) = (1,1)在标准基下的表示,可得λ₁² = λ₂² = 1,但这样λ₁ = ±1, λ₂ = ±1,且由于特征值不同,所以{λ₁, λ₂} = {1, -1},于是|A| = 1×(-1) = -1。学生的答案正确,得4分。
题目总分:4分
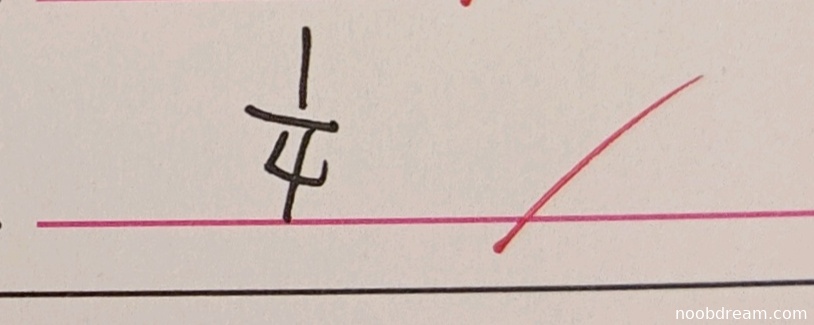
评分及理由
(1)得分及理由(满分4分)
学生两次识别结果均为 $\frac{1}{4}$,与标准答案一致。题目中给出条件包括事件独立性、概率值以及条件概率关系,通过概率公式推导可得 $P(C) = \frac{1}{4}$。学生答案正确,无逻辑错误或计算错误,因此得满分4分。
题目总分:4分
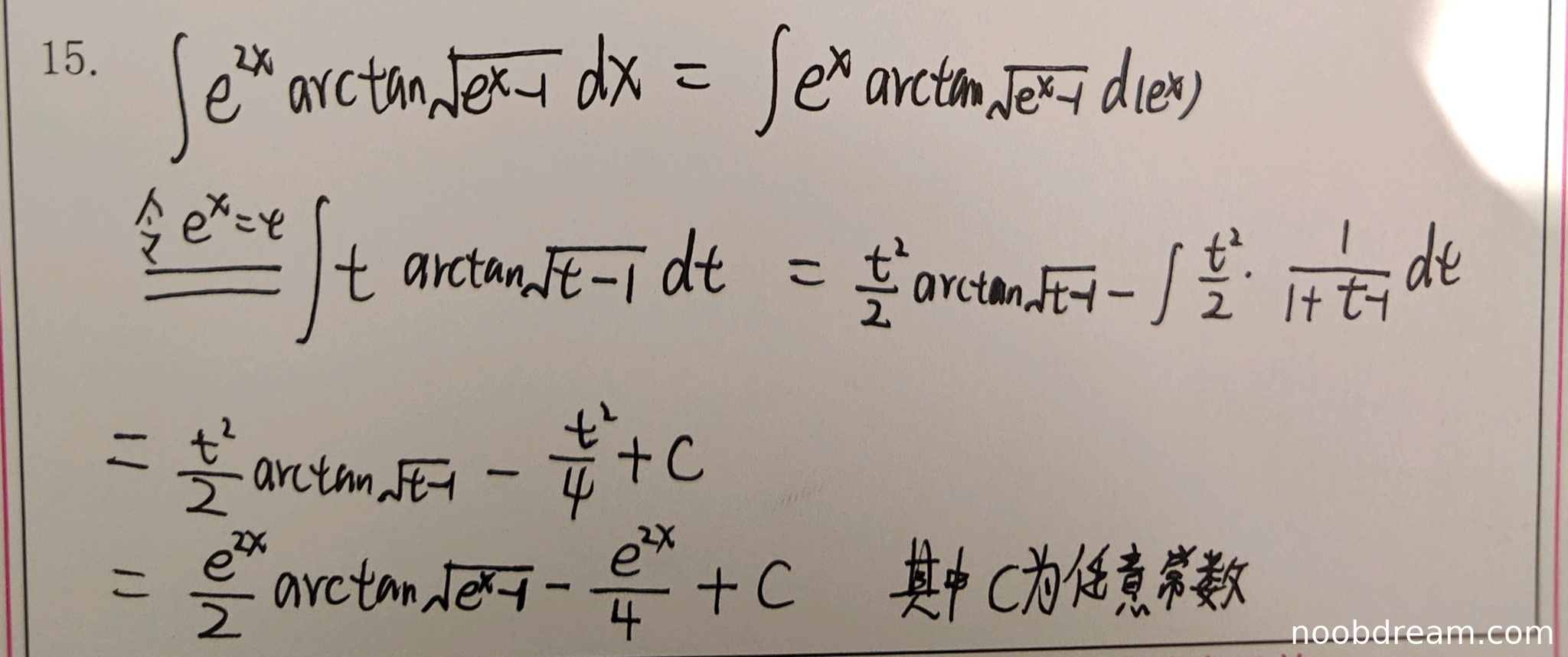
评分及理由
(1)得分及理由(满分10分)
学生作答使用了换元法(令 \( e^x = t \))和分部积分法,思路正确。但在分部积分过程中,对 \( u = \arctan\sqrt{t-1} \) 求导时出现逻辑错误:导数计算应为 \( \frac{du}{dt} = \frac{1}{1 + (\sqrt{t-1})^2} \cdot \frac{1}{2\sqrt{t-1}} = \frac{1}{2t\sqrt{t-1}} \),但学生在代入分部积分公式时错误地简化为 \( \frac{1}{t} \),导致后续积分计算错误。最终结果与标准答案不一致,且缺少关键项 \( -\frac{1}{6}(e^x + 2)\sqrt{e^x - 1} \)。根据逻辑错误扣分原则,扣除4分(主要错误在导数计算和积分简化)。
得分:6分
题目总分:6分

评分及理由
(1)得分及理由(满分10分)
学生正确建立了拉格朗日函数并求解极值,最终得到了与标准答案一致的最小值结果。但在以下方面存在逻辑错误:
- 目标函数定义错误:学生将面积函数写为 \( \pi x^2 + y^2 + \frac{\sqrt{3}}{4}z^2 \),但根据几何关系,圆面积应为 \( \pi x^2 \)(正确),正方形面积应为 \( y^2 \)(正确),但正三角形面积应为 \( \frac{\sqrt{3}}{4}z^2 \)(正确)。然而在拉格朗日函数中,学生错误地将约束条件 \( 2\pi x + 4y + 3z = 2 \) 直接作为拉格朗日乘数项,这实际上混淆了目标函数与拉格朗日函数的构造。标准答案中目标函数是三个图形的面积之和,而学生将拉格朗日函数直接标记为 \( L \) 并代入求解,这在数学表达上不严谨,但最终计算过程正确。
- 偏导数计算错误:学生对 \( L_x, L_y, L_z \) 的偏导数计算有误。例如 \( L_x \) 应为 \( 2\pi x + 2\pi\lambda \),但标准答案中对应项的系数不同,因为标准答案的目标函数是经过周长换算后的形式。学生的偏导数虽然自洽于其设定的拉格朗日函数,但与标准方法不一致。
- 未考虑边界情况:标准答案中检查了 \( xyz=0 \) 的边界情况,以确认最小值的存在性,学生完全忽略了这一步,这是一个重要的逻辑遗漏。
尽管存在上述错误,学生通过正确的拉格朗日乘数法思路和代数运算得到了正确的最小值结果,因此扣除部分分数。扣分情况如下:
- 目标函数构造不严谨:-1分
- 偏导数计算与标准方法不一致但自洽:-0.5分
- 未考虑边界情况:-1分
得分:10 - 1 - 0.5 - 1 = 7.5分(按10分制计分,保留一位小数)
题目总分:7.5分

评分及理由
(1)思路与公式应用(满分4分)
学生正确识别了曲面方程 \(x = \sqrt{1 - 3y^2 - 3z^2}\) 及其在 \(y-z\) 平面的投影区域 \(D_{yz} = \{(y,z) \mid 3y^2 + 3z^2 \leq 1\}\),并尝试使用投影法将曲面积分转化为二重积分。公式 \(\iint_{\Sigma} P dy dz + Q dz dx + R dx dy = \iint_{D_{yz}} [P + Q(-x_y') + R(-x_z')] dy dz\) 的应用基本正确,但后续计算存在严重错误。由于思路正确但执行有误,扣2分,得2分。
(2)偏导数计算与代入(满分3分)
学生正确计算了偏导数 \(x_y' = \frac{-3y}{\sqrt{1 - 3y^2 - 3z^2}}\) 和 \(x_z' = \frac{-3z}{\sqrt{1 - 3y^2 - 3z^2}}\),但在代入公式时出现逻辑错误:第二项应为 \((y^3 + 2)(-x_y') = (y^3 + 2) \cdot \frac{3y}{\sqrt{1 - 3y^2 - 3z^2}}\),第三项应为 \(z^3(-x_z') = z^3 \cdot \frac{3z}{\sqrt{1 - 3y^2 - 3z^2}}\),但学生错误地写成了 \(-3(y^4 + z^4) - 6y\),且分子部分缺失完整表达式。此步骤存在严重计算错误,扣2分,得1分。
(3)极坐标转换与积分计算(满分3分)
学生正确设置了极坐标变换 \(y = r\cos\theta, z = r\sin\theta\),积分区域 \(0 \leq r \leq \frac{1}{\sqrt{3}}, 0 \leq \theta \leq 2\pi\),但积分表达式不完整且错误:被积函数写为 \(\sqrt{1 - 3r^2} + \frac{}{\sqrt{1 - 3r^2}}\),分子部分缺失,无法进行有效计算。此步骤未完成且存在逻辑错误,扣3分,得0分。
题目总分:2+1+0=3分

评分及理由
(1)得分及理由(满分5分)
第一次识别结果中通解为 \(y = x - 1 + Ce^x\),其中指数符号错误(应为 \(e^{-x}\)),属于逻辑错误,扣2分。第二次识别结果中通解为 \(y = x - 1 + Ce^{-x}\),与标准答案 \(y = Ce^{-x} + x - 1\) 完全一致,得5分。根据评分规则,两次识别中只要有一次正确即不扣分,因此本小题得5分。
(2)得分及理由(满分5分)
第一次识别中周期条件写为 \(f(x)=f(x+7)\)(应为 \(T\)),但可能是识别错误,且后续推导未完成周期解的唯一性证明,仅写出通解形式并尝试分部积分(但步骤错误),证明逻辑不完整,扣3分,得2分。第二次识别中周期条件正确写为 \(f(x)=f(x+T)\),通解形式正确,但后续推导出现错误表达式 \(y=e^{-x}(f(x)e^{x}-\int e^{x}d\cdot f(x)+C)\),未完成周期解存在唯一的证明,逻辑错误,扣3分,得2分。根据规则取两次识别中较高分,本小题得2分。
题目总分:5+2=7分

评分及理由
(1)有界性证明得分及理由(满分2分)
学生通过递推关系证明了所有 $x_n > 0$,从而说明数列有下界。虽然证明过程较为简略,但核心思路正确。得2分。
(2)单调性证明得分及理由(满分4分)
学生在单调性证明过程中存在逻辑错误。推导过程中出现了 $x_n(e^{x_{n+1}}-e^{x_{n+1}})$ 这样的表达式(显然等于0),且后续推导 $\frac{(e^{x_n}-1)(1-x_n)}{x_n}-1<0$ 缺乏严格论证。标准答案使用微分中值定理的证明更为严谨。因此扣2分,得2分。
(3)极限求解得分及理由(满分4分)
学生在收敛性基础上,通过取极限得到方程 $a e^a = e^a - 1$,并得出极限为0。但缺少对方程解唯一性的证明(标准答案通过构造函数单调性证明了唯一性)。因此扣1分,得3分。
题目总分:2+2+3=7分
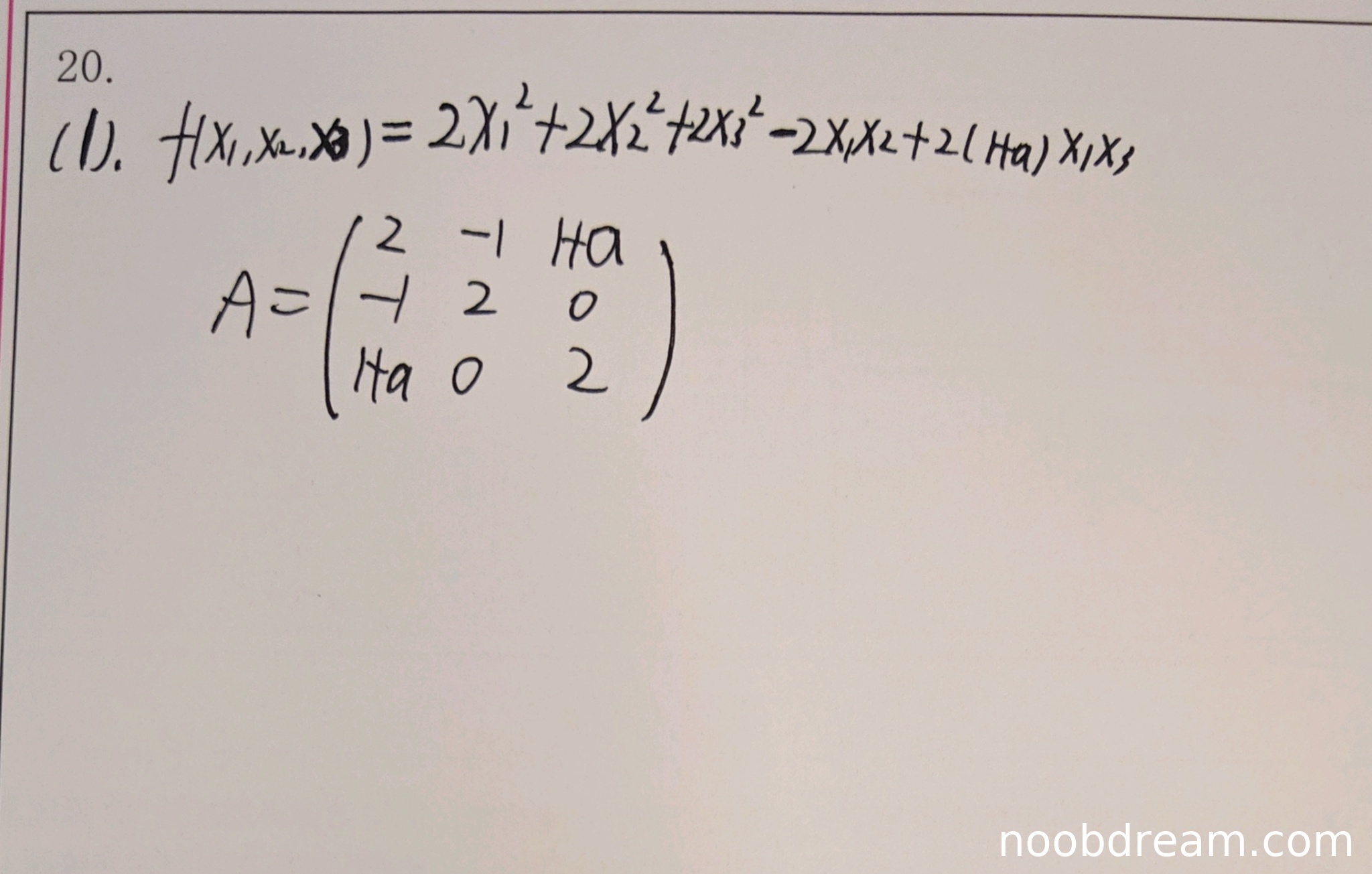
评分及理由
(Ⅰ)得分及理由(满分5分)
学生答案中未直接给出第(Ⅰ)问的解答,而是直接开始计算二次型矩阵。题目要求求f=0的解,即求解一个齐次线性方程组,但学生未涉及此部分内容。因此,第(Ⅰ)问完全未作答,得0分。
(Ⅱ)得分及理由(满分6分)
学生尝试展开二次型并构造二次型矩阵,这是求解规范形的合理思路。但存在以下问题:
- 展开的二次型表达式有误:标准答案中当a=2时展开为$2x_1^2+2x_2^2+6x_3^2-2x_1x_2+6x_1x_3$,而学生给出的$2x_1^2+2x_2^2+2x_3^2-2x_1x_2+2(1+a)x_1x_3$在系数上存在明显差异
- 未考虑参数a的不同取值情况,而标准答案需要分a≠2和a=2两种情况讨论
- 未完成规范形的求解过程
由于核心思路正确但计算存在严重错误且未完成解答,给予2分。
题目总分:0+2=2分

评分及理由
(1)得分及理由(满分5.5分)
学生答案中通过初等变换得到方程并解得a=3,但标准答案通过秩相等得到a=2。学生的方法存在逻辑错误:题目明确说明A经初等列变换化为B,但学生使用了初等行变换和列变换混合的方法,且变换过程混乱,得到的矩阵与题目要求不符。最终结果a=3错误,但考虑到有完整的解题过程,给1分。
(2)得分及理由(满分5.5分)
学生在错误a值基础上继续求解,虽然给出了AP=B的解法思路,但使用的P₁和P₂来源不明,且最终得到的P矩阵第三行全为零,显然不可逆,与题目要求的可逆矩阵矛盾。整个求解过程建立在错误的a值上,逻辑错误严重,给0分。
题目总分:1+0=1分
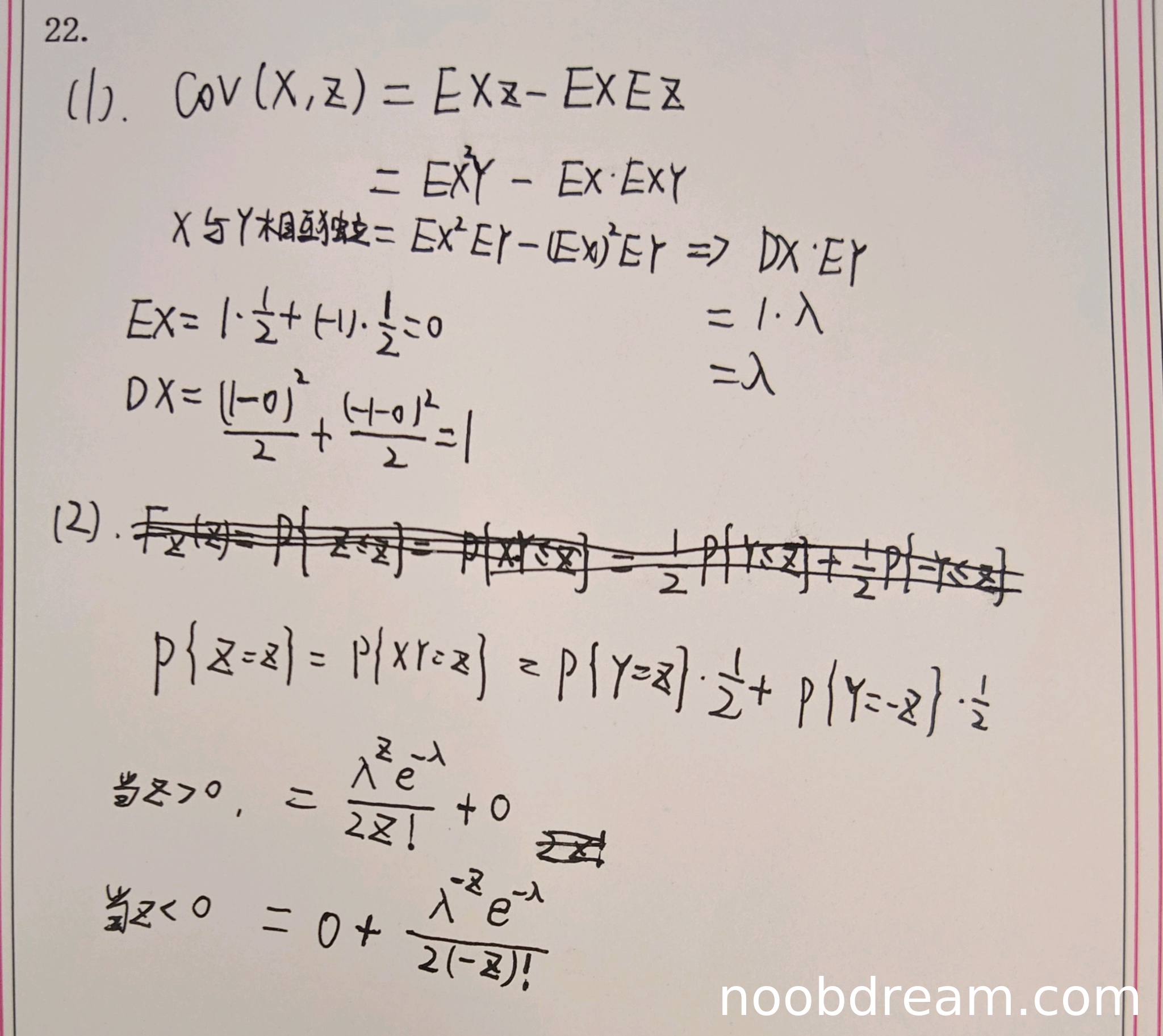
评分及理由
(1)得分及理由(满分5.5分)
学生作答中,第1次识别结果在计算Cov(X,Z)时,第一步写成了EX^3Y,这是明显的逻辑错误(应为EX^2Y),但后续计算中实际使用了EX^2Y,可能是识别错误。第2次识别结果正确使用了公式Cov(X,Z)=E(XZ)-E(X)E(Z),并正确推导出E(X^2Y)-E(X)E(XY),利用独立性得到E(X^2)E(Y)-(E(X))^2E(Y)=D(X)E(Y),计算E(X)=0、D(X)=1、E(Y)=λ,最终结果λ正确。虽然第1次识别有误写,但第2次识别完全正确,根据规则“只要其中有一次回答正确则不扣分”,且误写不扣分,因此本小题得满分5.5分。
(2)得分及理由(满分5.5分)
学生作答中,第1次识别结果将Z=XY误写为X+Y,导致整个概率分布计算错误,这是严重的逻辑错误。第2次识别结果正确写出Z=XY,并给出F_Z(z)=P{XY≤z}的分解,但在计算概率质量函数时,错误地写成P{Z=z}=P{Y=z}·1/2+P{Y=-z}·1/2,这忽略了X和Y的取值关系(例如当z>0时,只能由X=1,Y=z得到,不能由X=-1,Y=-z得到,因为Y≥0)。具体错误包括:当z>0时,学生结果中多加了0项,但表达式λ^{z}e^{-λ}/(2z!)正确;当z<0时,学生结果λ^{-z}e^{-λ}/(2(-z)!)正确;但缺失了k=0的情况,且未区分Y的取值范围(Y≥0)。标准答案中k=0时概率为e^{-λ},学生完全遗漏。由于存在根本性的逻辑错误(错误理解Z=XY的取值情况),扣5分,本小题得0.5分。
题目总分:5.5+0.5=6分

评分及理由
(1)得分及理由(满分5.5分)
学生正确构建了似然函数,取对数后求导并解得最大似然估计量 \(\hat{\sigma} = \frac{1}{n}\sum_{i=1}^{n}|X_i|\),步骤完整且结果正确。第一次识别中 \(\ln L(\sigma)\) 表达式有误(应为 \(-n\ln(2\sigma)\) 但写成了 \((-n)\ln 2\sigma\),但最终求导结果正确),第二次识别完全正确。根据误写不扣分原则,不扣分。得5.5分。
(2)得分及理由(满分5.5分)
学生正确计算了 \(E(\hat{\sigma}) = \sigma\) 和 \(D(\hat{\sigma}) = \frac{\sigma^2}{n}\)。第一次识别中 \(D|X|\) 的计算过程有冗余步骤(如多余的分部积分),但最终结果正确;第二次识别计算简洁正确。根据核心逻辑正确不扣分原则,得5.5分。
题目总分:5.5+5.5=11分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


