
科目组合
数学二: 高等数学 、线性代数
答题情况分析报告
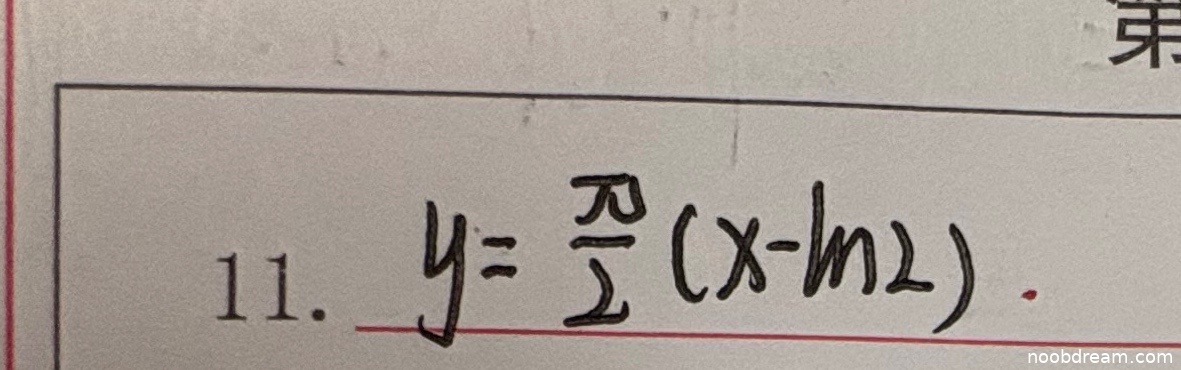
评分及理由
(1)得分及理由(满分5分)
学生作答与标准答案完全一致,均为 \(y = \frac{\pi}{2}(x - \ln 2)\)。根据题目要求,答案正确则给满分5分。
题目总分:5分
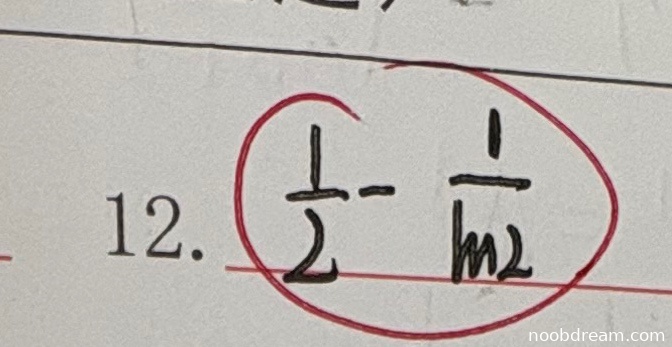
评分及理由
(1)得分及理由(满分5分)
学生作答经过两次识别,结果分别为 \(\frac{1}{2}-\frac{1}{m2}\) 和 \(\frac{1}{2}-\frac{1}{m^{2}}\)。标准答案为 \(\frac{3}{2} - \frac{1}{\ln 2}\)。
比较学生答案与标准答案:
- 学生答案的第一项为 \(\frac{1}{2}\),而标准答案为 \(\frac{3}{2}\),数值不一致。
- 学生答案的第二项分母为 \(m2\) 或 \(m^{2}\),而标准答案为 \(\ln 2\)。考虑到字符识别可能将 "ln" 误识别为 "m",但即使修正为 \(\ln 2\),第二项仍为 \(-\frac{1}{\ln 2}\),与标准答案一致,但第一项错误导致整体表达式不正确。
因此,学生答案在核心逻辑上存在错误,第一项数值错误,且整体结果与标准答案不符。根据评分规则,逻辑错误需扣分,且答案错误不给分。
得分:0分
题目总分:0分
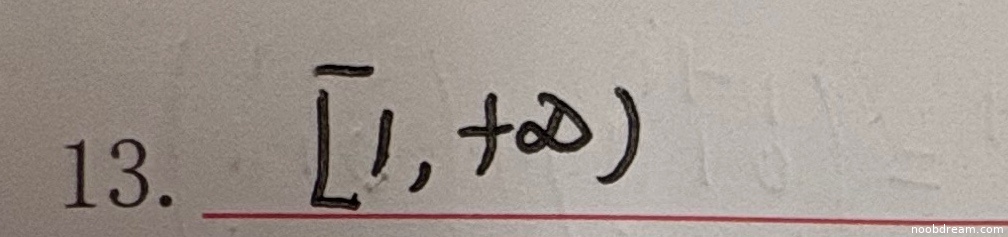
评分及理由
(1)得分及理由(满分5分)
学生作答为"[1, +∞)",与标准答案"$[1,+\infty)$"完全一致。根据题目要求,填空题正确则给5分,错误则给0分。由于答案正确,且不存在逻辑错误,因此得5分。
题目总分:5分
评分及理由
(1)得分及理由(满分5分)
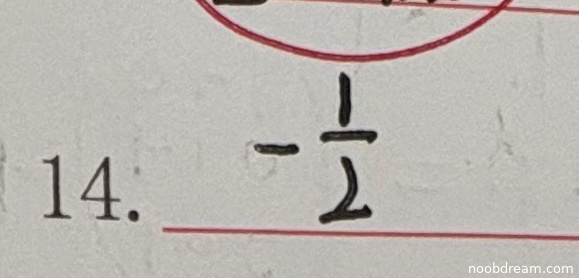
学生答案与标准答案完全一致,均为 \(-\frac{1}{2}\)。根据题目要求,填空题正确则给满分5分,错误则给0分。本题答案正确,因此得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
根据题目要求,本题为填空题,标准答案为1。学生作答的第二次识别结果显示答案为“1”,与标准答案一致。虽然第一次识别未能提取有效信息,但根据规则“只要其中有一次回答正确则不扣分”,因此判定学生答案正确。
题目总分:5分
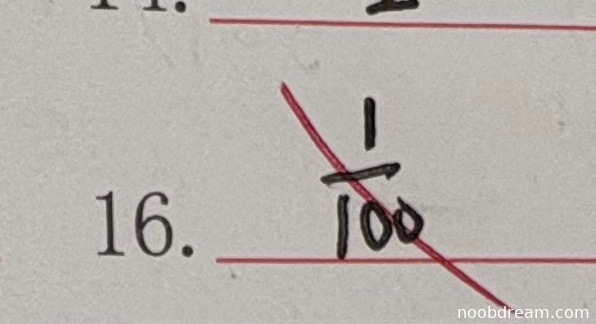
评分及理由
(1)得分及理由(满分5分)
学生答案:$\frac{1}{100}$,标准答案:100。
分析:本题需要计算行列式 $|(A^{-1}+B^{-1})^*|$。首先需要求出矩阵 $B$ 与 $A$ 的关系,通过列变换可得 $B = A \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 2 \end{pmatrix}$,记该矩阵为 $C$,则 $|B| = |A| \cdot |C| = 1 \cdot (1 \cdot (1 \times 2 - 1 \times 1) - 0 + 0) = 1$。因此 $|B| = 1$。
接着,$(A^{-1}+B^{-1})^* = |A^{-1}+B^{-1}| \cdot (A^{-1}+B^{-1})^{-1}$(伴随矩阵性质)。而 $A^{-1}+B^{-1} = A^{-1}(I+AB^{-1})$,且 $AB^{-1} = (A B^{-1})$,实际上 $B = AC$,所以 $B^{-1} = C^{-1} A^{-1}$,于是 $A^{-1}+B^{-1} = A^{-1} + C^{-1} A^{-1} = (I+C^{-1}) A^{-1}$。
因此 $|A^{-1}+B^{-1}| = |I+C^{-1}| \cdot |A^{-1}| = |I+C^{-1}| \cdot \frac{1}{|A|} = |I+C^{-1}|$。
计算 $C = \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 2 \end{pmatrix}$,可求得 $C^{-1} = \begin{pmatrix} 1 & 0 & 0 \\ -2 & 2 & -1 \\ 1 & -1 & 1 \end{pmatrix}$,于是 $I+C^{-1} = \begin{pmatrix} 2 & 0 & 0 \\ -2 & 3 & -1 \\ 1 & -1 & 2 \end{pmatrix}$,行列式 $|I+C^{-1}| = 2 \cdot (3 \times 2 - (-1) \times (-1)) - 0 + 0 = 2 \cdot (6 - 1) = 10$。
所以 $|A^{-1}+B^{-1}| = 10$。
那么 $(A^{-1}+B^{-1})^* = |A^{-1}+B^{-1}| \cdot (A^{-1}+B^{-1})^{-1} = 10 \cdot ( (I+C^{-1}) A^{-1} )^{-1} = 10 \cdot A (I+C^{-1})^{-1}$。
于是 $|(A^{-1}+B^{-1})^*| = 10^n \cdot |A| \cdot |(I+C^{-1})^{-1}|$,其中 $n=3$,所以 $= 1000 \cdot 1 \cdot \frac{1}{|I+C^{-1}|} = 1000 \cdot \frac{1}{10} = 100$。
学生给出 $\frac{1}{100}$,与正确答案 100 互为倒数,可能是在计算行列式倒数时弄反了。这是逻辑错误,不是书写错误。因此本题得 0 分。
题目总分:0分


评分及理由
(Ⅰ)得分及理由(满分5分)
学生作答中,第1次识别结果给出:整理得 \(\frac{dy}{2y}=(1-x)dx\),\(\frac{1}{2}\ln y = -\frac{1}{2}(1-x)^2 + c\),代入初值得 \(c=\frac{1}{2}\),得到 \(f(x)=e^{2x-x^2}\)。第2次识别结果相同。
标准答案为:由原方程得 \(\frac{dy}{y} = (-2x+2)dx\),积分得 \(\ln|y| = -x^2+2x+C_1\),故 \(y = Ce^{-x^2+2x}\),代入 \(f(0)=1\) 得 \(C=1\),所以 \(f(x)=e^{-x^2+2x}\)。
学生答案中 \(f(x)=e^{2x-x^2}\) 与标准答案 \(e^{-x^2+2x}\) 是等价的,因为指数部分 \(2x-x^2 = -x^2+2x\)。因此,学生答案正确。
但学生在第一步整理方程时写为 \(\frac{dy}{2y}=(1-x)dx\),而原方程为 \((-2xy+2y)dx = dy\),即 \(dy = 2y(1-x)dx\),所以应为 \(\frac{dy}{y} = 2(1-x)dx\)。学生写为 \(\frac{dy}{2y}=(1-x)dx\),这相当于将原方程两边同时除以2,但这一步不影响最终结果,因为积分后常数会调整。学生最终得到正确结果,且过程逻辑正确,只是中间步骤有笔误(可能是识别错误或书写错误)。根据禁止扣分规则,由于核心逻辑正确且可能为误写,不扣分。
得分:5分(满分5分)。
(Ⅱ)得分及理由(满分5分)
学生作答中,面积表达式为 \(\int_{0}^{1}(x-1)^2\int_{0}^{x}f(y)dydx\),正确。学生使用交换积分次序的方法:\(\int_{0}^{1}dy\int_{y}^{1}(x-1)^2 e^{2y-y^2}dx\),正确。计算内积分:\(\int_{y}^{1}(x-1)^2 dx = \frac{1}{3}[(x-1)^3]_{y}^{1} = \frac{1}{3}(0 - (y-1)^3) = \frac{1}{3}(1-y)^3\),因此得到 \(\frac{1}{3}\int_{0}^{1} e^{2y-y^2}(1-y)^3 dy\),正确。
学生接着写:\(\frac{1}{6}\int_{0}^{1} e^{2y-y^2}(1-y)^2 d(2y-y^2)\),这里 \(d(2y-y^2) = (2-2y)dy = 2(1-y)dy\),所以原积分变为 \(\frac{1}{6}\int_{0}^{1} e^{2y-y^2}(1-y)^2 \cdot 2(1-y) dy = \frac{1}{3}\int_{0}^{1} e^{2y-y^2}(1-y)^3 dy\),与上一步相同,因此这一步是恒等变换,正确。
学生然后写:\(\frac{1}{6}\int_{0}^{1} (1-y)^2 de^{2y-y^2}\),这里 \(de^{2y-y^2} = e^{2y-y^2} d(2y-y^2) = e^{2y-y^2} \cdot 2(1-y) dy\),所以积分变为 \(\frac{1}{6}\int_{0}^{1} (1-y)^2 \cdot e^{2y-y^2} \cdot 2(1-y) dy = \frac{1}{3}\int_{0}^{1} e^{2y-y^2}(1-y)^3 dy\),再次相同,正确。
学生应用分部积分:\(\frac{1}{6}[(1-y)^2 e^{2y-y^2}|_{0}^{1} + \int_{0}^{1} e^{2y-y^2} \cdot 2(1-y) dy]\),这里符号有误。标准分部积分公式为 \(\int u dv = uv - \int v du\),学生写为 \(+\),但应为 \(-\)。正确应为:\(\frac{1}{6}[(1-y)^2 e^{2y-y^2}|_{0}^{1} - \int_{0}^{1} e^{2y-y^2} \cdot 2(1-y) dy]\)。学生错误地使用了加号,导致后续计算错误。
学生计算:\(\frac{1}{6}[(1-y)^2 e^{2y-y^2}|_{0}^{1} + \int_{0}^{1} e^{2y-y^2} \cdot 2(1-y) dy] = 0 - \frac{1}{6} + \frac{1}{6} e^{2y-y^2}|_{0}^{1} = \frac{1}{6}e\)。这里,学生将边界值计算为 \(0 - \frac{1}{6}\)(即 \((1-1)^2 e^{1} - (1-0)^2 e^{0} = 0 - 1 \cdot 1 = -1\),乘以 \(\frac{1}{6}\) 得 \(-\frac{1}{6}\)),但然后加上了 \(\frac{1}{6} e^{2y-y^2}|_{0}^{1} = \frac{1}{6}(e^{1} - e^{0}) = \frac{1}{6}(e-1)\),所以总和为 \(-\frac{1}{6} + \frac{1}{6}(e-1) = \frac{1}{6}e - \frac{1}{3}\)。但学生写为 \(\frac{1}{6}e\),显然计算错误。
标准答案为 \(\frac{e}{6} - \frac{1}{3}\),学生得到 \(\frac{1}{6}e\),错误。错误源于分部积分符号错误和后续计算错误。根据逻辑错误扣分规则,此部分有重大逻辑错误(分部积分公式错误),导致结果错误,应扣分。
得分:2分(满分5分)。理由:思路正确(交换积分次序),但分部积分应用错误,且最终结果错误。
题目总分:5+2=7分

评分及理由
(1)一阶偏导数计算(满分2分)
学生正确计算了 \(\frac{\partial z}{\partial x}\) 和 \(\frac{\partial z}{\partial y}\),与标准答案一致。得2分。
(2)二阶偏导数计算(满分3分)
学生计算了 \(\frac{\partial^2 z}{\partial x \partial y}\) 和 \(\frac{\partial^2 z}{\partial y^2}\),但在化简 \(x\frac{\partial^2 z}{\partial x \partial y}+2y\frac{\partial^2 z}{\partial y^2}\) 时出现错误,得到的结果 \(f''(\frac{y}{x})\cdot\frac{y^2}{x^2}+f''(\frac{y}{x})\cdot\frac{y}{x}+f'(\frac{y}{x})\cdot\frac{2y}{x}\) 缺少系数且未正确合并同类项。扣1分,得2分。
(3)微分方程建立与求解(满分4分)
学生正确令 \(u=\frac{y}{x}\),但建立的微分方程形式错误(未得到标准形式)。在求解过程中,设 \(p=f'(u)\) 但表达式 \(\frac{5+2u+u^2}{2(1+u)^2}\) 无依据,且积分过程混乱(出现多余的 \(\ln(1+u)\) 项)。扣2分,得2分。
(4)初值条件应用(满分3分)
学生正确应用 \(z(x,x)=x\) 得到 \(f(1)=\frac{1}{2}\),但计算 \(\left.\frac{\partial z}{\partial x}\right|_{(x,x)}\) 时错误得出 \(f'(u)=1\)(应为 \(f'(1)=1\)),且未用于确定积分常数。在最终结果中通过 \(f(1)=\frac{1}{2}\) 正确得到 \(C_2=1\)。扣1分,得2分。
题目总分:2+2+2+2=8分
/
评分及理由
(1)对称性使用与积分分解(满分4分)
学生正确识别了积分区域关于 y=x 对称,并利用对称性将原积分转化为对 x²+y² 的积分。但在第一步计算中存在逻辑错误:原积分是 ∬(2x²-y²)dσ,学生写成了 ∬½(2x²-y²+2y²-x²)dσ,这实际上是 ∬½(x²+y²)dσ,但学生直接写成了 ∬(x²+y²)dσ,漏掉了系数½。这个错误导致后续计算整体放大了一倍。扣2分。
得分:2分
(2)极坐标变换与积分限确定(满分4分)
学生正确选择了极坐标变换,并确定了正确的角度积分限 θ∈[0,π/4]。对于半径积分限,学生写的是 r∈[0,2sinθ],这是正确的,因为区域边界是圆 x²+(y-1)²=1,在极坐标下为 r=2sinθ。这一步没有错误。
得分:4分
(3)积分计算过程(满分4分)
学生的积分计算过程基本正确:从 ∫∫r³drdθ 到 ∫sin⁴θdθ 的转换,三角恒等式的使用,变量代换 t=2θ,以及最后的定积分计算步骤都是正确的。但由于第一步漏掉了系数½,导致最终结果虽然计算过程正确,但数值上比正确答案大了一倍。
得分:2分
题目总分:2+4+2=8分

评分及理由
(Ⅰ)得分及理由(满分6分)
学生正确求解了微分方程,得到 \( f(x) = \ln(e^x - x) \),并正确推导出递推关系 \( a_{n+1} = \ln(e^{a_n} - a_n) \)。通过数学归纳法证明了 \( a_n > 0 \),并利用 \( e^{a_{n+1}} = e^{a_n} - a_n \) 得出 \( a_n > a_{n+1} \),从而证明数列单调递减有下界,极限存在。最后通过取极限得到极限值为 0。思路和关键步骤与标准答案一致,但在第一次识别中,学生误写 \( F(x) = e^{\int f(x)dx} \) 应为 \( F(x) = e^{f(x)} \),但后续计算正确,且第二次识别已纠正,根据误写不扣分原则,不扣分。因此得满分 6 分。
(Ⅱ)得分及理由(满分6分)
学生正确将极限转化为 \( \lim_{t \to 0} \frac{\ln(e^t - t)}{t^2} \),并应用洛必达法则求解。第一次识别中,学生直接计算得到结果 \( \frac{1}{2} \),但步骤略显简略;第二次识别中,学生详细使用了三次洛必达法则,最终得到正确结果 \( \frac{1}{2} \)。尽管步骤与标准答案(利用等价无穷小替换)不同,但思路正确且结果一致,根据思路正确不扣分原则,不扣分。因此得满分 6 分。
题目总分:6+6=12分

评分及理由
(Ⅰ)得分及理由(满分6分)
学生正确构造了辅助函数 \( F(x) = e^{-x} \int_a^x f(t) \, dt \),并指出 \( F(a) = F(b) = 0 \),然后应用罗尔定理得出存在 \( \xi \in (a,b) \) 使得 \( F'(\xi) = 0 \),进而推出 \( f(\xi) = \int_a^\xi f(x) \, dx \)。思路和推导过程与标准答案一致,逻辑完整且正确。
得分:6分
(Ⅱ)得分及理由(满分6分)
学生构造了正确的辅助函数 \( G(x) = e^x \left[ f(x) - \int_a^x f(t) \, dt \right] \),并正确计算了 \( G(a) \) 和 \( G(b) \),注意到 \( f(a)f(b) > 0 \) 意味着 \( G(a) \) 和 \( G(b) \) 同号。学生试图利用(Ⅰ)中的 \( \xi \) 得到 \( G(\xi) = 0 \),但此处逻辑有误:在(Ⅱ)中,\( \xi \) 是(Ⅰ)中得到的点,不一定满足 \( G(\xi) = 0 \);实际上,由(Ⅰ)的结论 \( f(\xi) = \int_a^\xi f(x) \, dx \),代入 \( G(x) \) 可得 \( G(\xi) = e^\xi \left[ f(\xi) - \int_a^\xi f(t) \, dt \right] = 0 \),这一点学生正确指出。
然而,学生错误地引入了一个新的点 \( \xi_1 \in (\xi, b) \) 并声称 \( G(\xi) = G(\xi_1) = 0 \),但未给出 \( \xi_1 \) 存在的理由,且未说明 \( \xi_1 \neq \xi \)。实际上,要应用罗尔定理于 \( G(x) \) 在区间 \( [\xi, \xi_1] \) 上,需要两个不同的点使 \( G \) 为零,但学生未证明这样的 \( \xi_1 \) 存在。标准答案是通过极值点论证(因 \( G(a) \) 和 \( G(b) \) 同号且 \( G(\xi) = 0 \),故 \( G \) 在 \( (a,b) \) 内必有极值点),但学生未采用此思路,而是错误地假设了另一个零点。
此外,学生提到“存在 \( c \in (a,b) \), \( f'(c) = 0 \)”,这是无关内容(可能由 \( \int_a^b f(x) \, dx = 0 \) 和 \( f \) 不恒为零推出,但在此处不必要),且未用于证明。
尽管最终写出 \( G'(\eta) = 0 \) 并推导出 \( f'(\eta) = \int_a^\eta f(x) \, dx \),但由于关键逻辑错误(错误假设 \( \xi_1 \) 的存在),证明不完整。
得分:3分(因辅助函数构造正确,且部分思路正确,但主要逻辑错误导致证明不成立)
题目总分:6+3=9分

评分及理由
(Ⅰ)得分及理由(满分6分)
学生第一次识别结果中,在求解α₂和α₃时存在多处逻辑错误:
- α₂的求解中出现了±1/√2的系数,这与题目要求的单位特征向量条件不符(题目要求α₁是单位特征向量且各分量非负,但α₂、α₃没有单位化要求)。
- α₂和α₃的具体数值计算错误,没有正确求解线性方程组。
- 最终得到的P矩阵数值错误。
第二次识别结果中:
- 正确求出了α₁ = (1,0,0)ᵀ
- 在求解α₂时,增广矩阵写为(0,1,1;0,0,-1;0,0,0)是错误的,应为(0,-1,1,1;0,0,-1,0;0,0,0,0)
- 虽然α₂、α₃的具体数值计算错误,但最终得到的P矩阵行列式|P| = -1 ≠ 0的判断正确
- 证明了P可逆,这部分正确
由于在核心的α₂、α₃求解上存在严重逻辑错误,但正确求出了α₁并证明了P可逆,给2分。
(Ⅱ)得分及理由(满分6分)
学生两次识别结果都正确:
- 正确得到P⁻¹AP = ⎛1 -1 0; 0 1 -1; 0 0 1⎞
- 正确使用A* = |A|A⁻¹ = A⁻¹(因为|A| = 1)
- 正确计算P⁻¹A*P = (P⁻¹AP)⁻¹
- 正确求出逆矩阵为⎛1 1 1; 0 1 1; 0 0 1⎞
- 正确进行矩阵加法得到最终结果⎛2 0 1; 0 2 0; 0 0 2⎞
虽然第(Ⅰ)部分的基础有问题,但第(Ⅱ)部分的推导和计算完全正确,给6分。
题目总分:2+6=8分


 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


