
科目组合
数学一: 高等数学 、线性代数 、概率论
答题情况分析报告
4
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是"4",与标准答案一致。函数$f(x,y)=x^{2}+2y^{2}$在点$(0,1)$处的梯度为$\nabla f=(2x,4y)$,在$(0,1)$处为$(0,4)$。最大方向导数为梯度的模,即$\sqrt{0^2+4^2}=4$。学生答案正确且计算无误,根据评分规则应得满分5分。
题目总分:5分
4
评分及理由
(1)得分及理由(满分5分)
学生答案:4
标准答案:4
理由:学生答案与标准答案完全一致。根据评分规则,填空题正确则给满分5分,错误则给0分。本题答案正确,因此得5分。
题目总分:5分
-1
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是-1,与标准答案完全一致。该题是填空题,直接考察对级数收敛域边界的计算,学生答案正确且无任何逻辑错误或计算过程错误。根据评分规则,正确则给满分5分。
题目总分:5分
-E
评分及理由
(1)得分及理由(满分5分)
学生作答为"-E",与标准答案"-E"完全一致。该答案表明学生正确推导出B - A的结果等于负单位矩阵。虽然题目没有要求写出推导过程,但最终结果正确,符合填空题的评分标准。根据规则"正确则给5分",本题得5分。
题目总分:5分
5/8
评分及理由
(1)得分及理由(满分5分)
学生答案:5/8
标准答案:5/8
评分理由:学生答案与标准答案完全一致。虽然学生没有展示解题过程,但根据题目要求这是填空题,只需给出最终结果。答案正确,符合评分标准中"正确则给5分"的要求。
题目总分:5分
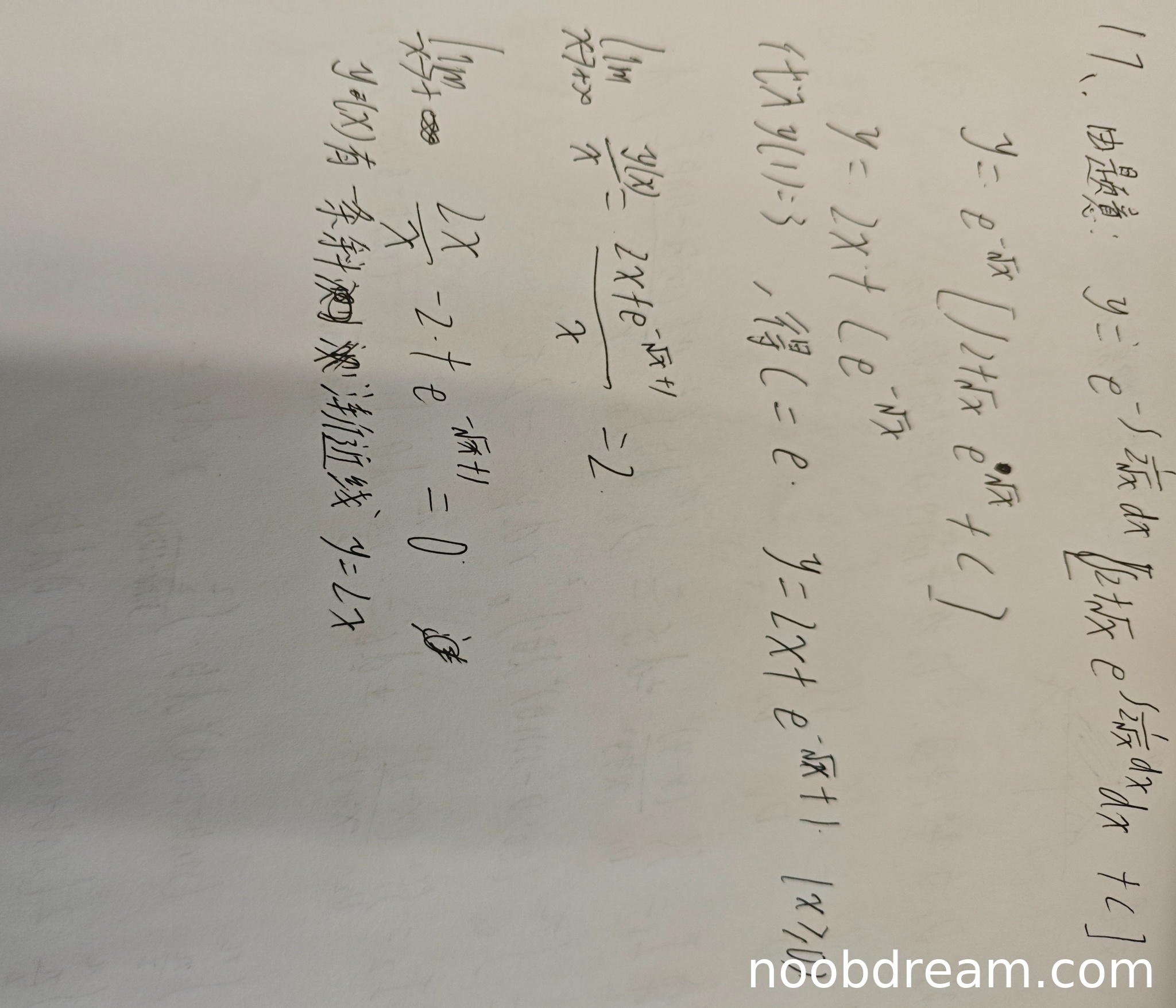
评分及理由
(1)第一次识别结果得分及理由(满分10分)
第一次识别结果中,学生正确求解了微分方程,得到通解形式 \( y = 2x + C e^{-\sqrt{x}} \),并利用初值条件 \( y(1) = 3 \) 确定常数 \( C = e \),得到特解 \( y = 2x + e^{1 - \sqrt{x}} \)。随后正确计算了斜渐近线:斜率 \( k = \lim_{x \to +\infty} \frac{y}{x} = 2 \),截距 \( b = \lim_{x \to +\infty} (y - 2x) = 0 \),得出斜渐近线为 \( y = 2x \)。整个过程逻辑正确,计算无误。但未讨论铅直渐近线和水平渐近线,属于步骤不完整,扣1分。得分:9分。
(2)第二次识别结果得分及理由(满分10分)
第二次识别结果中,学生从错误的微分方程出发(误写为 \( y' = e^x \) 等),导致后续求解完全错误,与题目无关。虽然最后提到渐近线,但基于错误函数得出错误结论。整个解答逻辑错误,与标准答案无关。得分:0分。
题目总分:9+0=9分

评分及理由
(1)得分及理由(满分12分)
学生采用了两步识别结果,其中第一次识别结果存在多处逻辑错误:
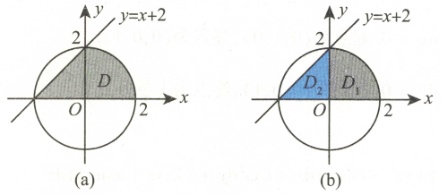
- 定义区域D₁和D₂不清晰,且D₂的积分限错误(直线边界应为r=2/(sinθ-cosθ),但学生写成了r=0到2)
- 计算过程中出现错误表达式"2(cosθ-sinθ)²/(sinθ-cosθ)",这不符合积分运算规则
- 最后的计算步骤混乱,缺乏清晰的逻辑链条
第二次识别结果有明显改进:
- 正确采用了"整个半圆减去部分区域"的思路
- 对D₁(整个半圆)的计算基本正确,得到2π
- 但对D₂的区域定义和积分限设置错误(θ范围应为π/2到π,r范围应为0到2/(sinθ-cosθ))
- D₂的计算过程中积分限和表达式均错误
- 最终结果π+2与正确答案2π-2不符
考虑到学生:
- 正确识别了极坐标变换
- 采用了合理的解题思路(整体减部分)
- 对D₁的计算基本正确
- 但关键的区域划分和D₂的计算存在严重错误
给予6分(满分12分)
题目总分:6分

评分及理由
(1)思路分析
学生采用了与标准答案法一相似的思路,将曲线L分解为三个坐标平面上的线段L₁、L₂、L₃分别计算。这种思路是正确的,符合题目要求。
(2)具体计算过程
在L₁的计算中:学生得出I₁ = -1/2,这与标准答案中L₁的积分结果1/2在数值上相等但符号相反,说明学生可能对积分方向理解有误。标准答案中从(1/2,0,0)到(0,1,0)的积分结果为1/2,而学生计算为-1/2,这是方向错误导致的。
在L₂的计算中:学生得出I₂ = 0,这与标准答案一致,正确。
在L₃的计算中:学生的计算过程较为混乱,出现了路径无关性的分析,但最终未能正确计算出I₃的值。标准答案中I₃ = -1/2,而学生未能得出正确结果。
(3)最终结果
学生最终得出I = 1,而正确答案应为0。这说明虽然思路基本正确,但在具体计算和方向判断上存在多处错误。
扣分点:
- L₁积分方向错误,导致符号错误
- L₃计算过程混乱且结果错误
- 最终结果错误
考虑到本题满分12分,学生基本思路正确但计算存在较多错误,给予部分分数。
题目总分:4分

评分及理由
(1)得分及理由(满分4分)
学生第一次识别给出的矩阵为 $\begin{pmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{pmatrix}$,与标准答案一致;第二次识别给出的矩阵为 $\begin{pmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 4 \end{pmatrix}$,其中最后一个元素应为9但误写为4,但根据上下文和第一次识别结果,可判断为识别错误。由于至少有一次正确,且核心逻辑正确,不扣分。得4分。
(2)得分及理由(满分6分)
学生正确判断出矩阵的秩为1,特征值为0,0,14。但在计算特征向量时存在多处错误:
- 对于特征值0,学生给出的基础解系 $\xi_1=(1,-1,1)^T$ 和 $\xi_2=(5,-4,1)^T$ 不满足方程 $x_1+2x_2+3x_3=0$(例如 $\xi_1$ 代入得 $1-2+3=2\neq0$),因此特征向量计算错误。
- 对于特征值14,学生给出的 $\xi_3=(1,1,1)^T$ 不满足 $(14E-A)X=0$(例如第一行:$13-2-3=8\neq0$),因此特征向量计算错误。
- 正交化和单位化过程基于错误的特征向量,因此整个正交变换矩阵 $Q$ 错误,最终对角矩阵的顺序(0,0,14)与标准答案(14,0,0)不一致,但考虑到特征值正确,且正交变换思路正确,部分步骤可得分。
由于特征值正确(得2分),但特征向量全部错误,正交变换结果错误,扣4分。得2分。
(3)得分及理由(满分2分)
学生未作答第(Ⅲ)问,得0分。
题目总分:4+2+0=6分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


