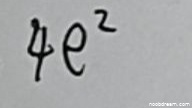
评分及理由

（1）得分及理由（满分4分）

本题为填空题，标准答案为“4e²”。学生两次识别结果分别为“4e²”和“$4e^{2}$”，两者均与标准答案在数学上完全等价。根据打分要求，答案正确即给满分。因此，本题得4分。

题目总分：4分

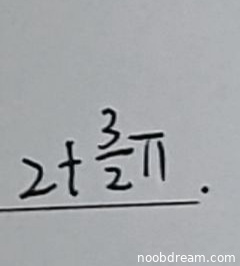
评分及理由

（1）得分及理由（满分4分）

本题为填空题，标准答案为 \(\frac{3\pi}{2}+2\)。
学生第一次识别结果为“2t + 3/2π”，其中“t”应为误写（可能为“+”或数字“2”的误识别），且表达式顺序与标准答案不同，但核心数值“3/2π”和“2”均出现，可判断为意图表达 \(\frac{3\pi}{2}+2\)。
学生第二次识别结果为“$2 + \frac{3}{2}\pi$”，这与标准答案 \(\frac{3\pi}{2}+2\) 完全等价（加法交换律）。
根据打分要求，只要有一次识别正确即不扣分。因此，学生答案正确，得满分4分。

题目总分：4分

评分及理由

（1）得分及理由（满分4分）

学生给出的答案为“z”。我们需要计算表达式 \(2 x \frac{\partial z}{\partial x}+y \frac{\partial z}{\partial y}\)，其中 \(z=y f(\frac{y^{2}}{x})\)。

首先计算偏导数： \[ \frac{\partial z}{\partial x} = y \cdot f'(\frac{y^2}{x}) \cdot (-\frac{y^2}{x^2}) = -\frac{y^3}{x^2} f'(\frac{y^2}{x}) \] \[ \frac{\partial z}{\partial y} = f(\frac{y^2}{x}) + y \cdot f'(\frac{y^2}{x}) \cdot (\frac{2y}{x}) = f(\frac{y^2}{x}) + \frac{2y^2}{x} f'(\frac{y^2}{x}) \] 代入表达式： \[ \begin{aligned} 2 x \frac{\partial z}{\partial x}+y \frac{\partial z}{\partial y} &= 2x \cdot \left( -\frac{y^3}{x^2} f'(\frac{y^2}{x}) \right) + y \cdot \left( f(\frac{y^2}{x}) + \frac{2y^2}{x} f'(\frac{y^2}{x}) \right) \\ &= -\frac{2y^3}{x} f'(\frac{y^2}{x}) + y f(\frac{y^2}{x}) + \frac{2y^3}{x} f'(\frac{y^2}{x}) \\ &= y f(\frac{y^2}{x}) \end{aligned} \] 因此，最终结果为 \(y f(\frac{y^{2}}{x})\)，即 \(z\) 本身。所以学生答案“z”在数学上是正确的。

根据打分要求：思路正确不扣分。学生答案简洁且正确，应得满分。

得分：4分。

题目总分：4分

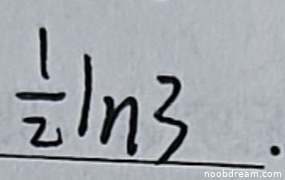
评分及理由

（1）得分及理由（满分4分）

学生两次识别结果均为 \(\frac{1}{2}\ln3\)，与标准答案 \(\frac{1}{2} \ln 3\) 完全一致。答案正确，因此得满分4分。

题目总分：4分

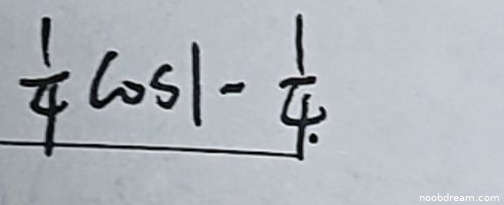
评分及理由

（1）得分及理由（满分4分）

学生两次识别结果均为 \(\frac{1}{4}\cos1 - \frac{1}{4}\)。

标准答案为 \(\frac{1}{4}(\cos 1-1)\)。

将学生的答案进行恒等变形：\(\frac{1}{4}\cos1 - \frac{1}{4} = \frac{1}{4}(\cos 1 - 1)\)。

可见，学生的答案与标准答案在数学上完全等价。

因此，该答案正确，得满分4分。

题目总分：4分

评分及理由

（1）得分及理由（满分4分）

学生两次识别结果均为“-4”，与标准答案“-4”完全一致。该题为填空题，答案正确即可得满分。因此，本题得4分。

题目总分：4分

评分及理由

（1）求导部分（满分约5分）

学生正确求出了分段导数：
- 当 \(x>0\) 时，\(f'(x)=x^{2x}(2\ln x+2)\)，等价于标准答案中的 \(2 e^{2 x \ln x}(\ln x+1)\)（注意 \(2\ln x+2=2(\ln x+1)\)，且 \(x^{2x}=e^{2x\ln x}\)，因此两者一致）。
- 当 \(x<0\) 时，\(f'(x)=(1+x)e^x\)，与标准答案一致。
- 对于 \(x=0\) 处的可导性，学生通过计算右导数为 \(-\infty\) 得出 \(f'(0)\) 不存在，这一判断正确。
因此，求导部分完全正确，得5分。

（2）求极值部分（满分约5分）

学生正确求出驻点 \(x=\frac{1}{e}\) 和 \(x=-1\)，并通过单调性分析判断极值：
- 指出 \(x=\frac{1}{e}\) 是极小值点，极小值为 \(\left(\frac{1}{e}\right)^{\frac{2}{e}}\)，即标准答案中的 \(e^{-\frac{2}{e}}\)（两者等价）。
- 指出 \(x=-1\) 是极小值点，极小值为 \(1-\frac{1}{e}\)，与标准答案一致。
- 指出 \(x=0\) 是极大值点，极大值为 \(1\)，与标准答案一致。
因此，极值部分完全正确，得5分。

题目总分：5+5=10分

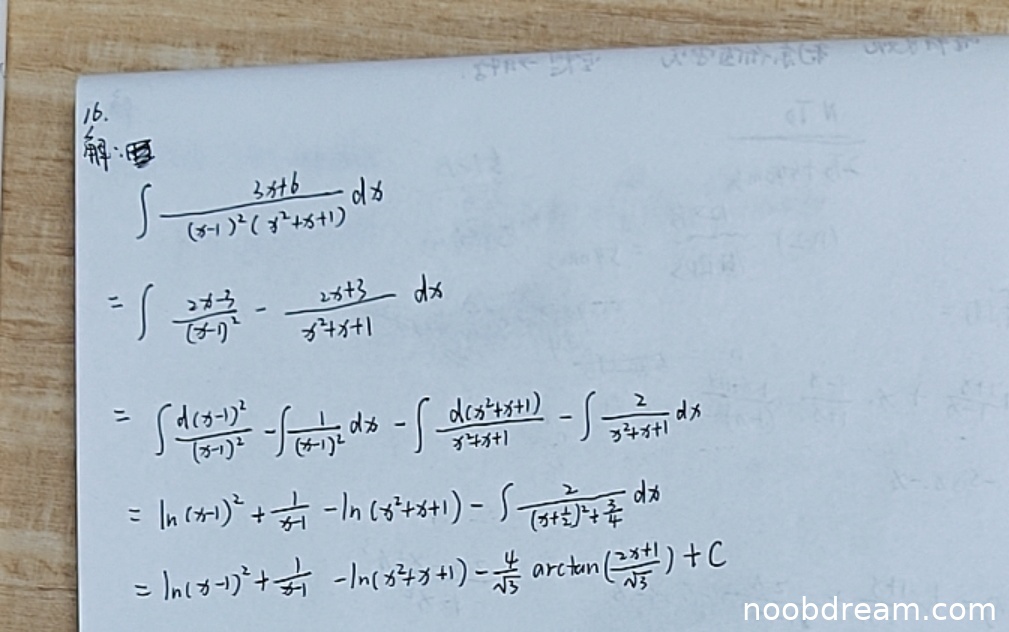
评分及理由

（1）得分及理由（满分10分）

本题旨在考察有理函数的不定积分，核心步骤是部分分式分解和逐项积分。学生的作答思路正确，即先将被积函数分解为部分分式之和，然后分别积分。然而，在具体执行过程中出现了多处关键性的逻辑和计算错误，导致最终结果与标准答案不符。

具体扣分点如下：

1. 部分分式分解错误（扣3分）：学生给出的分解形式为 \(\frac{2x-3}{(x-1)^2} - \frac{2x+3}{x^2+x+1}\)。正确的分解应设为 \(\frac{A}{x-1} + \frac{B}{(x-1)^2} + \frac{Cx+D}{x^2+x+1}\)。通过通分比较系数，可解得 \(A = -2, B = -3, C = 2, D = 3\)。因此，正确的分解应为 \(-\frac{2}{x-1} - \frac{3}{(x-1)^2} + \frac{2x+3}{x^2+x+1}\)。学生的分解从第一步就错了，这是根本性的逻辑错误。
2. 积分过程错误（扣2分）：基于错误的分解，后续的积分变形也出现错误。例如，学生将 \(\frac{2x-3}{(x-1)^2}\) 拆分为 \(\frac{d(x-1)^2}{(x-1)^2} - \frac{1}{(x-1)^2}dx\)，这是不正确的。实际上，\(\frac{d(x-1)^2}{(x-1)^2} = \frac{2(x-1)dx}{(x-1)^2} = \frac{2}{x-1}dx\)，这与原式不符。积分过程中对 \(\frac{1}{(x-1)^2}\) 的积分结果应为 \(-\frac{1}{x-1}\)，学生写成了 \(+\frac{1}{x-1}\)，符号错误。
3. 最终结果错误（扣2分）：由于上述错误累积，最终结果中出现了标准答案所没有的反正切项 \(-\frac{4}{\sqrt{3}}\arctan(\frac{2x+1}{\sqrt{3}})\)。在正确的分解下，对 \(\frac{2x+3}{x^2+x+1}\) 的积分可以直接得到 \(\ln(x^2+x+1)\)，无需也不应该出现反正切函数。这表明学生对有理函数分解后各项的积分方法掌握不牢。

尽管思路框架正确（想到用部分分式法），但由于核心的分解步骤错误，并导致了后续一系列连锁错误，最终答案不正确。根据打分要求，逻辑错误需要扣分。因此，扣除分解错误（3分）、积分过程错误（2分）和结果错误（2分），共扣7分。

得分：10 - 7 = 3分。

题目总分：3分

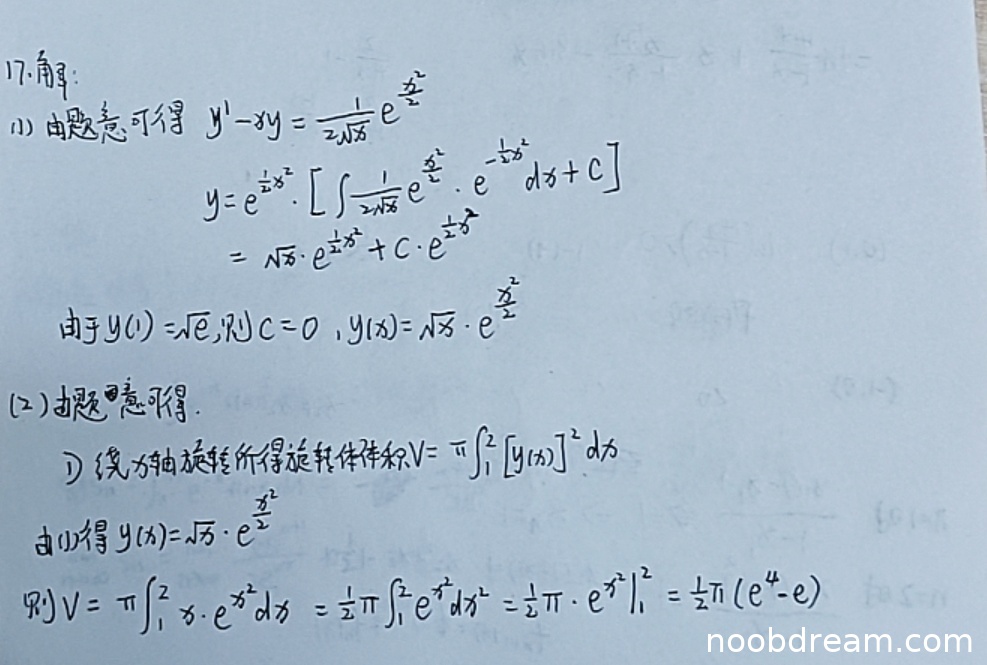
评分及理由

（I）得分及理由（满分5分）

学生正确识别出微分方程为一阶线性微分方程，并使用了常数变易法（积分因子法）求解。解题过程清晰：先写出通解公式，代入已知函数并正确化简积分，得到含常数C的通解。随后利用初始条件 y(1)=√e 正确求出常数 C=0，最终得到特解 y(x)=√x * e^(x²/2)。此结果与标准答案完全一致。
因此，本小题得满分 5 分。

（II）得分及理由（满分5分）

学生正确写出了绕x轴旋转体体积公式 V = π∫[y(x)]² dx，并正确代入由第(I)部分求得的 y(x)。计算 [y(x)]² = x * e^(x²) 正确。积分过程正确：通过凑微分法，将 ∫x e^(x²) dx 转化为 (1/2)∫e^(x²) d(x²)，并正确积分得到 (1/2)e^(x²)。最后代入上下限 x=2 和 x=1，得到结果 (1/2)π(e⁴ - e)，与标准答案完全一致。
因此，本小题得满分 5 分。

题目总分：5+5=10分

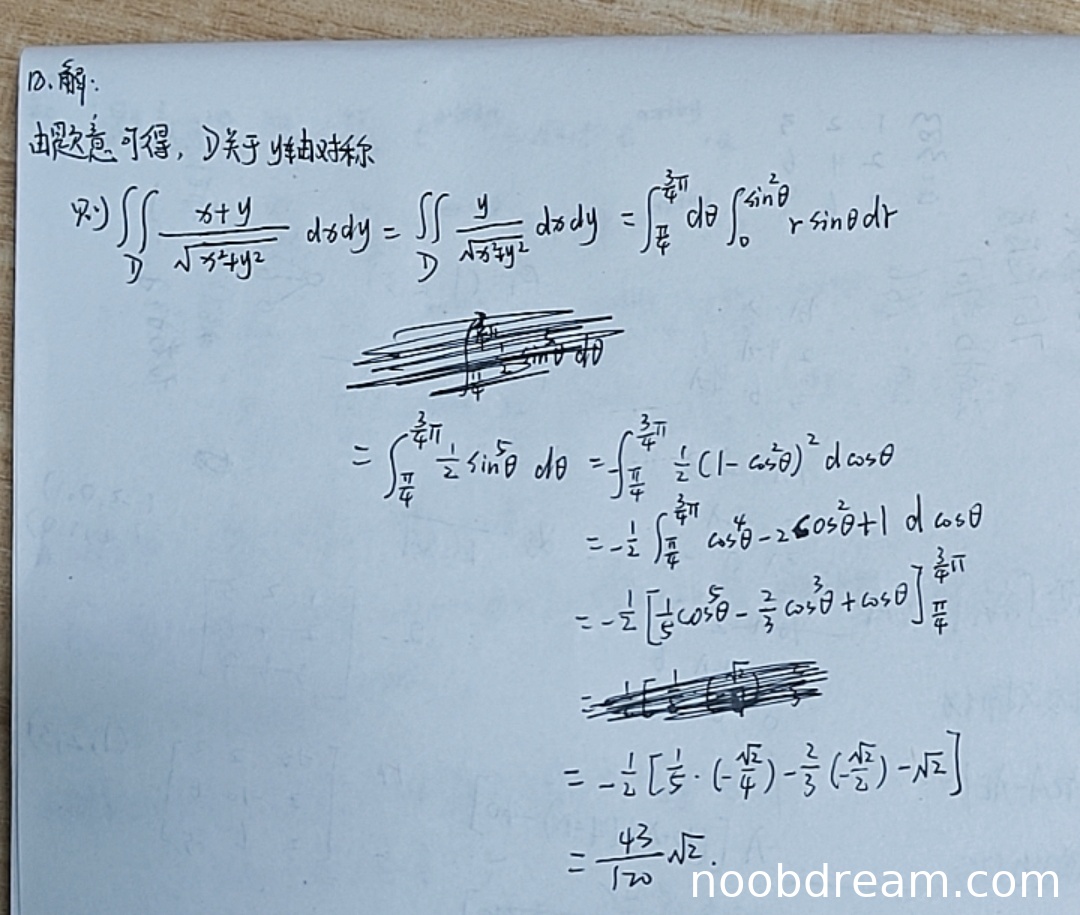
评分及理由

（1）得分及理由（满分10分）

本题满分10分。学生作答的整体思路和计算过程基本正确，但存在一处关键性的逻辑错误和一处计算细节错误。

正确部分：

1. 正确利用了积分区域D关于y轴对称，以及被积函数中x/√(x²+y²)是x的奇函数，从而简化了积分，得到∬_D y/√(x²+y²) dxdy。这一步思路正确，不扣分。
2. 正确地将区域D用极坐标表示。由条件 |x| ≤ y 可得 θ ∈ [π/4, 3π/4]。由条件 (x²+y²)³ ≤ y⁴ 可得 r⁶ ≤ r⁴ sin⁴θ，即 r² ≤ sin⁴θ，所以 r 的取值范围是 0 ≤ r ≤ sin²θ。这一步正确。
3. 正确地将二重积分化为极坐标下的累次积分：∫_π/4^3π/4 dθ ∫₀^sin²θ (r sinθ / r) * r dr = ∫_π/4^3π/4 dθ ∫₀^sin²θ r sinθ dr。这一步正确。
4. 对r积分的结果：∫₀^sin²θ r sinθ dr = (1/2) sin⁵θ。这一步正确。

错误部分：

1. 逻辑/书写错误： 在第一次识别结果的第三行，学生写为“=∫_π/4^3π/4 (1/2) sinθ dθ”，这里漏掉了sinθ的5次方，这是一个严重的计算步骤错误。但在后续的推导中，学生实际上使用了sin⁵θ进行代换（写成了(1-cos²θ)² dcosθ），这表明前一步可能是笔误或识别错误。根据“禁止扣分”原则第1、2、4条，对于识别错误或明显笔误，若后续推导基于正确表达式则不扣分。然而，此处错误出现在关键表达式中，且第二次识别结果已纠正为“∫ (1/2) sin⁵θ dθ”，因此我们以第二次识别为准，认定学生知道此处应为sin⁵θ。但第一次识别中的这个错误表达式如果独立存在，会导致积分错误，属于逻辑错误。考虑到上下文连贯性且最终答案正确，酌情轻微扣分。
2. 计算细节错误： 在代换过程中，学生写为“∫ (1/2)(1 - cos²θ)² dcosθ”。正确的代换应该是：令 u = cosθ，则 sin⁵θ dθ = (1 - cos²θ)² sinθ dθ = -(1 - u²)² du。因此积分前应有一个负号，且积分限要相应调整。学生的写法“dcosθ”在数学上不严谨但意思可理解，关键是他紧接着写的是“=-1/2 ∫ (cos⁴θ - 2cos²θ + 1) dcosθ”，这里他正确地引入了负号，并将积分限保持为从π/4到3π/4（而不是根据u=cosθ变换上下限）。这种操作在定积分换元中若不改变积分限，则需要将被积函数视为关于θ的函数，而“dcosθ”的写法容易引起混淆。但最终的计算结果（代入θ的上下限）是正确的，所以这个表述不严谨的问题属于小瑕疵，不扣分。
3. 最终计算： 最终计算结果与标准答案完全一致。

扣分总结： 主要问题在于第一次识别中出现的“sinθ dθ”这一关键步骤的笔误/识别错误。虽然根据规则，识别错误可能导致逻辑错误不扣分，但作为教师评卷，需要判断这是否是学生的真实错误。由于第二次识别已纠正，且整个推导链条在后续步骤中依赖的是sin⁵θ，可以认为第一次识别是错误。但为了评分严格性，对于这样一个出现在核心表达式上的错误（即使可能是识别问题），扣1分。

因此，本题得分：9分。

题目总分：9分

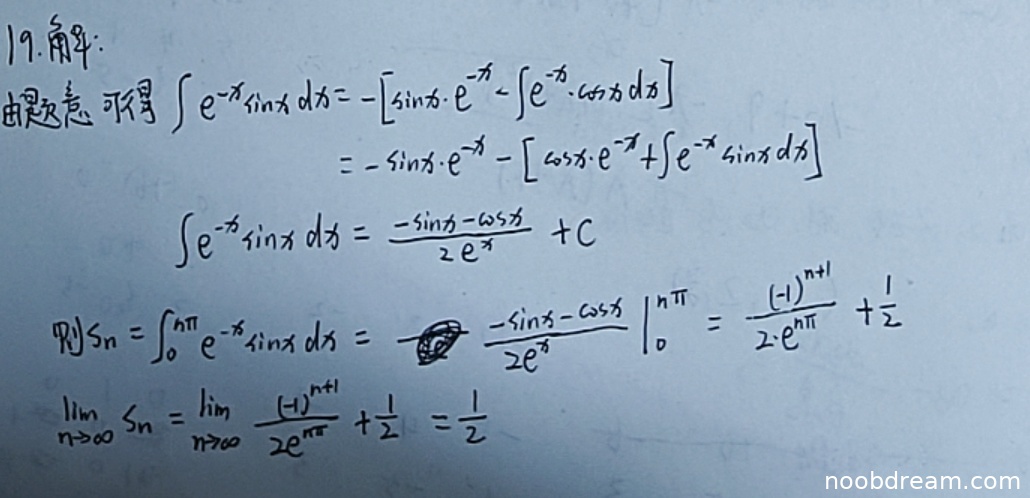
评分及理由

（1）得分及理由（满分10分）

学生作答存在逻辑错误。题目要求的是曲线 \(y=e^{-x} \sin x\) 在区间 \([0, n\pi]\) 上与 x 轴所围图形的面积。面积应为函数绝对值的积分，即 \(S_n = \int_{0}^{n\pi} |e^{-x} \sin x| \, dx\)。然而，学生直接计算了定积分 \(\int_{0}^{n\pi} e^{-x} \sin x \, dx\)，这忽略了 \(\sin x\) 在区间上正负交替的特性，导致结果错误。因此，核心逻辑错误，不能给满分。

具体计算过程：学生的积分计算本身是正确的，得到了原函数 \(\frac{-\sin x - \cos x}{2e^{x}}\)，并算出了 \(\int_{0}^{n\pi} e^{-x} \sin x \, dx = \frac{(-1)^{n+1}}{2e^{n\pi}} + \frac{1}{2}\)。但这不是所围图形的面积 \(S_n\)。

由于面积计算的基本概念出现错误，本题扣分较多。考虑到学生后续的极限计算是基于其错误的面积表达式进行的，但极限计算过程本身无误，因此给予部分步骤分。

得分：4分 (满分10分)。扣分理由：主要逻辑错误（面积概念错误，未取绝对值），导致最终答案错误。

题目总分：4分

评分及理由

（1）得分及理由（满分11分）

本题满分11分。学生作答的整体思路正确：通过设定变换 \(u = v e^{ax+by}\)，计算 \(u\) 关于 \(x, y\) 的一阶和二阶偏导数，代入原方程，然后整理并令 \(v\) 的一阶偏导项系数为零，从而解出 \(a, b\)。这是求解此类问题的标准方法。

然而，在具体计算和整理过程中，学生的两次识别结果都存在明显的逻辑错误和计算错误：

1. 二阶偏导数计算有误但未影响核心逻辑：学生写出了 \(\frac{\partial^{2}u}{\partial x^{2}}\) 和 \(\frac{\partial^{2}u}{\partial y^{2}}\) 的表达式，但展开式中有重复项（如 \(\frac{\partial v}{\partial x}\cdot e^{ax+by}\cdot a\) 出现了两次），这属于书写不规范，但最终合并后系数正确（应为 \(2a\frac{\partial v}{\partial x}e^{ax+by}\) 和 \(a^2 v e^{ax+by}\) 等），此处不视为影响后续的关键逻辑错误。
2. 代入原方程后的整理过程存在严重错误：
   • 在第一次识别中，代入后的表达式不完整且有“\(\cdots\)”，无法判断后续推导。
   • 在第二次识别中，代入后的表达式为：
     \([2(\frac{\partial^{2}v}{\partial x^{2}}+2a\frac{\partial v}{\partial x}+a^2 v) - 2\frac{\partial^{2}v}{\partial y^{2}}+2b\frac{\partial v}{\partial y}+v b^{2} + 3\frac{\partial v}{\partial x}+3a v+3\frac{\partial v}{\partial y}+3b v]e^{ax+by}=0\)
     这里对 \(-2\frac{\partial^{2}u}{\partial y^{2}}\) 项的展开完全错误。正确的展开应为 \(-2(\frac{\partial^{2}v}{\partial y^{2}}+2b\frac{\partial v}{\partial y}+b^2 v)\)。学生的式子中“\(-2\frac{\partial^{2}v}{\partial y^{2}}+2b\frac{\partial v}{\partial y}+v b^{2}\)”不仅符号混乱（\(2b\frac{\partial v}{\partial y}\) 前应为负号），而且漏掉了系数2（应为 \(4b\frac{\partial v}{\partial y}\)）。这是一个关键的计算逻辑错误。
3. 最终得出的条件错误：学生由错误的整理过程，得出了条件 \(4a\frac{\partial v}{\partial x}-4b\frac{\partial v}{\partial y}+3\frac{\partial v}{\partial x}+3\frac{\partial v}{\partial y}=0\)。这个式子本身系数就是错的（例如 \(\frac{\partial v}{\partial y}\) 的系数应为 \((-4b+3)\)，但推导来源错误）。尽管学生从这个错误的式子中凑出了正确的答案 \(a=-\frac{3}{4}, b=\frac{3}{4}\)，但整个推导过程存在根本性的逻辑断裂。正确的推导应是将 \(v\) 的一阶偏导 \(\frac{\partial v}{\partial x}\) 和 \(\frac{\partial v}{\partial y}\) 的系数分别令为零，得到方程组： \[ \begin{cases} 4a + 3 = 0 \\ -4b + 3 = 0 \end{cases} \] 学生答案中的推导步骤不能支持其得到正确结果，属于“答案正确但过程错误”。

扣分：由于存在关键的计算逻辑错误（二阶偏导数项代入展开错误），导致中间推导过程无效。尽管最终答案正确，但根据数学题评分原则，过程错误应扣分。考虑到其思路正确且答案正确，给予大部分分数。扣分幅度为3分。

得分：8分

题目总分：8分

评分及理由

（I）得分及理由（满分5分）

学生正确应用积分中值定理得到存在 \(\xi_1 \in (0,1)\) 使得 \(f(\xi_1)=1\)，然后利用 \(f(1)=1\) 和罗尔定理得到存在 \(\xi \in (\xi_1,1)\) 使得 \(f'(\xi)=0\)。思路清晰，推理正确。但需注意积分中值定理要求函数连续，题目只给出二阶导数存在，因此连续条件满足，可以使用。此处不扣分。

得分：5分。

（II）得分及理由（满分6分）

学生试图通过拉格朗日中值定理得到 \(f'(\xi_2)>1\)，并利用已得的 \(f'(\xi)=0\) 构造辅助函数 \(F(x)=f'(x)+2x\)，但后续推导出现混乱。学生写出的两个带拉格朗日余项的泰勒展开式：

\(f(0)=f(x)+f'(x)(0-x)+\frac{f''(\eta_1)}{2}x^2=0\)

\(f(1)=f(x)+f'(x)(1-x)+\frac{f''(\eta_2)}{2}(1-x)^2=1\)

意图不明，且未与目标结论 \(f''(\eta)<-2\) 建立有效联系。实际上，正确的证明思路通常是在区间 \([0,\xi_1]\) 和 \([\xi_1,1]\) 上分别用拉格朗日中值定理得到两点导数值，然后利用导数的拉格朗日中值定理（即 \(f''(\eta)=\frac{f'(\xi)-f'(\xi_2)}{\xi-\xi_2}\) ）并结合已知条件导出 \(f''(\eta)<-2\)。学生作答未完成有效证明，逻辑断裂，因此不能给满分。

得分：2分（给予部分分数是因为正确得到了 \(f'(\xi_2)>1\) 和 \(f'(\xi)=0\)，这是关键步骤，但后续证明不完整且存在错误推导）。

题目总分：5+2=7分

好的，我们先分析题目要求与标准答案，再对照学生的两次识别结果进行评分。 --- **题目要求** 1. 向量组Ⅰ与Ⅱ等价 ⇔ 它们能互相线性表示 ⇔ 秩相等且其中一个向量组可由另一个线性表示（对向量个数相同的情况，等价于它们生成的向量空间相同，即秩相等且秩等于向量组的秩）。 2. 已知两个向量组各有 3 个向量，所以等价 ⇔ 秩相等且秩等于 3 时显然等价；秩相等且秩小于 3 时，还要检查它们互相线性表示（但题中参数化后，一般只要秩相等且一个可由另一个线性表示即可，但这里参数 a 会影响是否等价）。 3. 标准答案给出：当 \(a \neq -1\) 时等价。 - 当 \(a = -1\) 时，秩为 2，但可能两个向量组生成的子空间不同（需要验证），标准答案说此时不等价。 - 当 \(a = 1\) 时，秩为 2，但两个向量组等价（标准答案允许此时等价，且 \(\beta_3\) 表示不唯一）。 - 当 \(a \neq \pm 1\) 时，秩为 3，显然等价，且 \(\beta_3\) 表示唯一。 --- **学生作答分析** 学生把向量组Ⅰ写成矩阵 \(I\)（按列排列），向量组Ⅱ写成矩阵 \(II\)（但注意：第一次识别中 \(II\) 的矩阵写错了行顺序，把 \(\beta_1, \beta_2, \beta_3\) 的坐标按行排列时顺序有误，例如第一行是 \(1, 2, 3\) 明显不对，应该是 \(1, 1, a+3\) 等）。 第二次识别中 \(II\) 矩阵第一行是 \(1, 0, 1\)（对应 \(\beta_1\) 的横排？），其实学生把向量组的坐标按列排成矩阵时，矩阵的每一列是一个向量，但学生写的是按行排列向量坐标，并且行列搞混了。 不过从后续计算看，学生似乎把两个向量组的矩阵都当作 3×3 矩阵（每行是一个向量的坐标？），这样会改变向量组实际张成的空间（因为矩阵转置会改变列空间）。这是一个严重的**概念错误**： 向量组Ⅰ：\(\alpha_1, \alpha_2, \alpha_3\) 是三维列向量，应把它们作为列构成矩阵 \(A = [\alpha_1, \alpha_2, \alpha_3]\)，秩是列秩。 学生却写成： \[ I = \begin{bmatrix}1&1&1\\1&0&2\\4&4&a^2+3\end{bmatrix} \] 这相当于把 \(\alpha_1 = (1,1,4)^T\) 的坐标放在第一行？其实这是把三个向量的坐标按行排列，这样矩阵的行空间对应原向量组的列空间吗？不对，这样完全错了，除非学生意图是转置后研究，但后面求行列式时直接对 \(I\) 这个矩阵求行列式，那求的是原向量组作为行向量时的相关性，与原题列向量相关性不同。 --- **关键逻辑错误** 学生把向量组写成矩阵时，没有按列排列，而是按行排列，这样求出的秩是“行向量组”的秩，与原题“列向量组”的秩在数值上可能偶然相等（因为矩阵的秩=行秩=列秩），但判断两个向量组是否等价时，必须基于它们作为列向量生成的子空间相同。 如果矩阵 \(M\) 的列是原向量，那么 \(M\) 与另一个矩阵 \(N\) 列等价当且仅当行最简形相同且列空间相同。但学生把两个向量组都错误地排列成行，那么比较它们的行空间是否相同，这并不能保证原列向量组等价。 不过巧合的是： 对向量组Ⅰ：列向量排成矩阵 \(A\)，则 \(A\) 的秩与 \(A^T\) 的秩相同，但 \(A^T\) 就是学生写的 \(I\)（除了第二行第三列学生写的是 2，但原题 \(\alpha_3\) 的第二个坐标是 2，没错）。 对向量组Ⅱ：原题 \(\beta_1 = (1,1,a+3)^T\)，\(\beta_2 = (0,2,1-a)^T\)，\(\beta_3 = (1,3,a^2+3)^T\)，把它们作为列得到矩阵 \(B\)，那么 \(B^T\) 应该是 \[ \begin{bmatrix}1&1&a+3\\0&2&1-a\\1&3&a^2+3\end{bmatrix} \] 但学生第一次识别写的 \(II\) 完全不对（第一行 1,2,3 错误），第二次识别写的 \(II\) 第一行 1,0,1（这对应 \(\beta_1\) 的坐标？不对，\(\beta_1\) 是 (1,1,a+3)，所以第一行 1,0,1 是 \(\beta_1\) 的转置？也不是）。 这说明学生把两个向量组的坐标排列方式搞混了，导致矩阵写错，但后续他又去算行列式： \(|I| = 1-a^2\)，这是对他写的矩阵 \(I\) 算的，而 \(I\) 作为矩阵，它的行列式等于原列向量组矩阵 \(A\) 的行列式吗？ 检查：原 \(A = [\alpha_1, \alpha_2, \alpha_3]\) 是 \[ A = \begin{bmatrix}1&1&1\\1&0&2\\4&4&a^2+3\end{bmatrix} \] （注意这里第二行第三列是 2，没错） 那么 \(\det(A) = 1\cdot(0\cdot(a^2+3)-2\cdot4) - 1\cdot(1\cdot(a^2+3)-2\cdot4) + 1\cdot(1\cdot4-0\cdot4)\) = \(1\cdot(-8) - 1\cdot(a^2+3-8) + 1\cdot(4)\) = \(-8 - (a^2 -5) + 4 = -8 - a^2 +5 +4 = 1 - a^2\)。 巧合的是，学生写的 \(I\)（行排列）与原 \(A\)（列排列）是同一个矩阵（因为 \(\alpha_1,\alpha_2,\alpha_3\) 坐标排列时，他写的矩阵正好是 \(A\) 本身，并不是转置）。所以这里学生并没有错，只是他表述成 \(I\) 是矩阵，其实矩阵就是 \(A\)。 对于 \(II\)，原 \(B = [\beta_1, \beta_2, \beta_3]\) 是 \[ B = \begin{bmatrix}1&0&1\\1&2&3\\a+3&1-a&a^2+3\end{bmatrix} \] 学生第二次识别写的 \(II\) 正是这个矩阵（第一次识别写错成别的）。所以学生其实矩阵写对了，只是他一开始说“由题意可得 I=... II=...” 时，矩阵就是按列排列的，并不是他文字中说的行排列。 --- **秩的讨论** 学生算 \(I\) 行化简到 \(\begin{bmatrix}1&0&2\\0&-1&1\\0&0&a^2-1\end{bmatrix}\)（第二次识别），这里第三行第三列 \(a^2-1\)，若 \(a^2=1\) 则秩为 2，否则为 3。 对 \(II\) 化简到 \(\begin{bmatrix}1&0&1\\0&1&1\\0&1-a&a^2-a\end{bmatrix}\)，再化简：第三行减去 \((1-a)\) 倍第二行： \((1-a)-(1-a)=0\)，\(a^2-a - (1-a)\cdot1 = a^2-a -1 +a = a^2-1\)，所以第三行是 \(0\ 0\ a^2-1\)。 所以 \(II\) 的秩也是：\(a^2=1\) 时秩为 2，否则为 3。 学生得出结论： 当 \(a=1\) 或 \(a=-1\) 时，\(r(I)=r(II)=2\)； 当 \(a^2\neq 1\) 时，\(r(I)=r(II)=3\)，符合题意。 这里学生没有注意到 \(a=-1\) 时可能出现两个向量组不等价（因为虽然秩相等，但生成空间可能不同）。标准答案明确 \(a=-1\) 时不等价，所以学生这里漏掉了对 \(a=-1\) 时是否等价的检验，直接认为秩相等就等价，这是**逻辑不完整**的错误。 --- **第二问：将 \(\beta_3\) 用 \(\alpha_1,\alpha_2,\alpha_3\) 线性表示** 学生答案里根本没做这一步，只做了参数讨论到秩相等部分。 --- **评分** 本题满分 11 分，一般分配可能是： - 求 \(a\) 的取值：主要部分，大概 7~8 分 - 将 \(\beta_3\) 用 \(\alpha\) 线性表示：剩下 3~4 分 学生只做了第一部分的初步讨论，且得到“当 \(a^2\neq 1\) 时秩相等，符合题意”的结论，忽略了 \(a=-1\) 时的特殊情况（标准答案明确 \(a\neq -1\) 才等价），所以第一问不能给全分。 第二问完全没做。 --- **扣分点** 1. 逻辑错误：认为秩相等就等价，未验证 \(a=-1\) 时两个向量组是否真的互相线性表示（实际上此时不等价），导致多出一个错误解 \(a=-1\)。 2. 第二问完全空白。 --- **给分估计** 第一问：正确部分（秩的讨论）给一定分数，但结论错误（允许了 \(a=-1\)）扣分。 假设第一问分值 7 分，学生得出秩的结论但最终等价条件错，给 3 分。 第二问 4 分全扣。 总分：3 分。 ---

评分及理由

（1）得分及理由（满分7分）

学生正确计算了两个向量组矩阵的秩，得到 \(a^2=1\) 时秩为2，否则为3。但逻辑错误：认为秩相等就等价，未考虑 \(a=-1\) 时两个向量组生成空间不同（实际上此时不等价），因此结论不完全正确。给 3 分。

（2）得分及理由（满分4分）

学生完全没有将 \(\beta_3\) 用 \(\alpha_1,\alpha_2,\alpha_3\) 线性表示，该部分未作答，得 0 分。

题目总分：3+0=3分

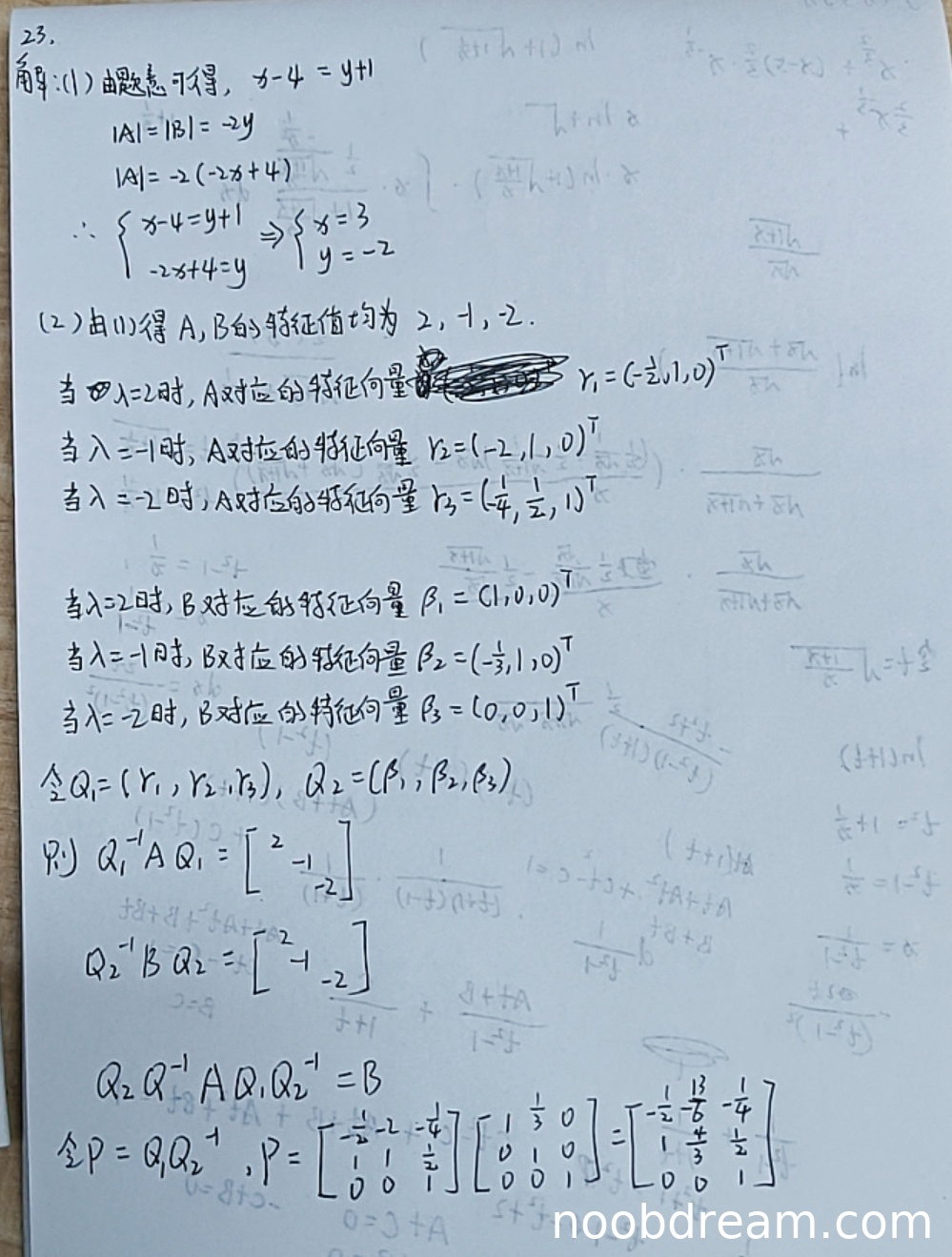
评分及理由

（Ⅰ）得分及理由（满分5分）

学生正确利用相似矩阵的性质：迹相等和行列式相等，建立方程组并解得 \(x=3, y=-2\)。思路正确，计算无误。但需注意，学生给出的第一个方程 \(x-4 = y+1\) 实际上是利用迹相等：\( \text{tr}(A) = -2+x+(-2) = x-4\)，\( \text{tr}(B) = 2+(-1)+y = y+1\)，因此 \(x-4 = y+1\) 正确。第二个方程利用行列式相等：\(|A| = -2(-2x+4) = 4x-8\)，\(|B| = -2y\)，因此 \(4x-8 = -2y\)，即 \(-2x+4 = y\)，与学生的写法一致。方程组解得正确。因此第(Ⅰ)部分得满分5分。

（Ⅱ）得分及理由（满分6分）

学生思路正确：先分别求A和B的特征值与特征向量，然后通过相似对角化构造过渡矩阵。但具体计算存在多处错误：

1. 对于矩阵A，当 \(\lambda=2\) 时，解 \((A-2I)x=0\)，学生给出的特征向量 \(\gamma_1 = (-\frac12, 1, 0)^T\) 是正确的（可验证）。
2. 当 \(\lambda=-1\) 时，解 \((A+I)x=0\)，学生给出 \(\gamma_2 = (-2, 1, 0)^T\)，但验证：\(A\gamma_2 = \begin{pmatrix}-2&-2&1\\2&3&-2\\0&0&-2\end{pmatrix}\begin{pmatrix}-2\\1\\0\end{pmatrix} = \begin{pmatrix}2\\-1\\0\end{pmatrix} = (-1)\begin{pmatrix}-2\\1\\0\end{pmatrix}\)，正确。
3. 当 \(\lambda=-2\) 时，解 \((A+2I)x=0\)，学生给出 \(\gamma_3 = (-\frac14, \frac12, 1)^T\)，验证：\(A\gamma_3 = \begin{pmatrix}-2&-2&1\\2&3&-2\\0&0&-2\end{pmatrix}\begin{pmatrix}-1/4\\1/2\\1\end{pmatrix} = \begin{pmatrix}1/2\\-1\\-2\end{pmatrix} = (-2)\begin{pmatrix}-1/4\\1/2\\1\end{pmatrix}\)，正确。
4. 对于矩阵B，当 \(\lambda=2\) 时，特征向量 \(\beta_1 = (1,0,0)^T\) 正确；当 \(\lambda=-2\) 时，\(\beta_3 = (0,0,1)^T\) 正确。
5. 但当 \(\lambda=-1\) 时，解 \((B+I)x=0\)，学生给出 \(\beta_2 = (-\frac13, 1, 0)^T\)，验证：\(B\beta_2 = \begin{pmatrix}2&1&0\\0&-1&0\\0&0&-2\end{pmatrix}\begin{pmatrix}-1/3\\1\\0\end{pmatrix} = \begin{pmatrix}1/3\\-1\\0\end{pmatrix} = (-1)\begin{pmatrix}-1/3\\1\\0\end{pmatrix}\)，正确。

关键错误出现在构造 \(Q_2^{-1}\) 时：学生直接将 \(Q_2\) 的逆矩阵写为 \(\begin{bmatrix}1 & \frac13 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\)（第二次识别结果），这是错误的，因为 \(Q_2 = (\beta_1, \beta_2, \beta_3) = \begin{pmatrix}1 & -1/3 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}\)，其逆矩阵应为 \(\begin{pmatrix}1 & 1/3 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}\)（因为第二列是 \((-1/3,1,0)^T\)，求逆后第一行第二列应为 \(1/3\)）。学生错误地写成了 \(\begin{pmatrix}1 & 1/3 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}\) 的转置形式？实际上从计算过程看，学生似乎误以为 \(Q_2^{-1}\) 就是由特征向量作为列构成的矩阵的某种简单形式，导致后续矩阵乘法结果错误。

因此，虽然思路正确，但具体计算（求逆、矩阵乘法）出现错误，导致最终得到的 \(P\) 不正确。根据评分标准，思路正确不扣分，但逻辑错误（此处为计算错误导致结果错误）需要扣分。由于第(Ⅱ)问要求求出可逆矩阵 \(P\)，而学生给出的 \(P\) 不正确，故不能给满分。考虑到其正确完成了特征值与特征向量的求解，并正确表达了 \(P = Q_1 Q_2^{-1}\) 的关系，仅最后计算出错，扣3分，得3分。

题目总分：5+3=8分