
科目组合
数学二: 高等数学 、线性代数
答题情况分析报告

评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(\frac{1}{e}\),与标准答案完全一致。根据评分规则,答案正确即得满分。尽管题目要求禁止给步骤分,但本题为填空题,仅以最终答案为准。因此,本题得5分。
题目总分:5分
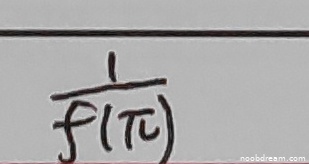
评分及理由
(1)得分及理由(满分5分)
学生两次识别给出的答案均为 \(\frac{1}{f(\pi)}\)。题目要求计算 \(f(x)\) 在 \([0, \pi]\) 上的平均值,即 \(\frac{1}{\pi} \int_{0}^{\pi} f(x) dx\)。学生的答案形式与所求量完全不同,且 \(\frac{1}{f(\pi)}\) 是一个与函数在单点值有关的表达式,并非所要求的积分平均值。这表明学生未能正确理解题意或解题过程存在根本性错误,没有得出与标准答案 \(\frac{\sqrt{6}}{4}\) 相关的任何正确中间结果或最终结果。因此,本题得分为0分。
题目总分:0分
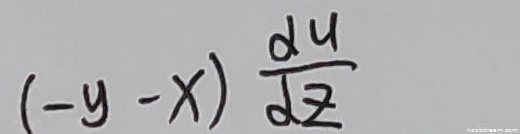
评分及理由
(1)得分及理由(满分5分)
学生答案为:\((-y - x)\frac{du}{dz}\)。
标准答案为:\(f_{1}'+f_{2}'-(x+y)f_{3}'\)。
分析:题目要求计算 \(\frac {\partial u}{\partial x}+\frac {\partial u}{\partial y}\)。学生答案的表达式 \((-y - x)\frac{du}{dz}\) 存在以下问题:
- 符号表示错误:学生使用了常微分符号 \(\frac{du}{dz}\),但 \(u\) 是 \(x, y, z\) 的函数,而 \(z\) 又是 \(x, y\) 的函数,因此这里应是偏导数 \(\frac{\partial u}{\partial z}\) 或 \(f_3'\)。使用 \(\frac{du}{dz}\) 在多元函数链式法则的上下文中是不规范的,且可能暗示对 \(z\) 的全导数,这与题意不符。
- 缺失关键项:根据链式法则,\(\frac{\partial u}{\partial x} = f_1' + f_3' \cdot \frac{\partial z}{\partial x}\),\(\frac{\partial u}{\partial y} = f_2' + f_3' \cdot \frac{\partial z}{\partial y}\)。因此,\(\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y} = f_1' + f_2' + f_3' \cdot (\frac{\partial z}{\partial x} + \frac{\partial z}{\partial y})\)。学生答案仅给出了 \(f_3'\) 乘以一个系数的形式,完全缺失了 \(f_1'\) 和 \(f_2'\) 项。
- 系数可能来源:学生答案中的系数 \((-y-x)\) 与标准答案中 \(-(x+y)\) 在数值上相等。这可能是学生正确地从隐函数方程 \(\int_{0}^{xy+z}e^{-t^{2}}dt=1\) 求出了 \(\frac{\partial z}{\partial x} = -y\) 和 \(\frac{\partial z}{\partial y} = -x\),从而得到 \(\frac{\partial z}{\partial x} + \frac{\partial z}{\partial y} = -(x+y)\)。这表明学生可能理解了隐函数求导的部分,但严重忽略了链式法则中关于 \(f\) 对第一个和第二个中间变量的偏导项,这是一个根本性的逻辑错误。
根据打分要求,对于逻辑错误需要扣分。学生的答案没有正确应用多元复合函数求导的链式法则,核心逻辑不完整且符号使用不当,因此不能得分。
得分:0分
题目总分:0分
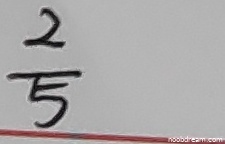
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(\frac{2}{5}\),与标准答案 \(\frac {2}{5}\) 完全一致。根据打分要求,答案正确即得满分。题目为填空题,无步骤分要求,因此直接根据最终答案评判。学生答案正确,得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
学生给出的答案为 \(\sqrt{x}\) 或 √x,两者均表示 \(y = \sqrt{x}\)。该答案与标准答案 \(\sqrt{x}\) 完全一致,且满足初始条件 \(y(1)=1\)。因此,本题答案正确,得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为“3”,与标准答案“3”完全一致。根据题目要求,本题为填空题,答案正确即得5分。学生的作答没有展示过程,仅给出最终结果,但结果正确,因此得满分5分。
题目总分:5分

评分及理由
(Ⅰ)得分及理由(满分4分)
学生正确证明了 \(F(t+T)=F(t)\),并指出 \(F(t)\) 是以 \(T\) 为周期的连续函数。证明过程与标准答案一致,逻辑清晰。因此得满分 4 分。
(Ⅱ)得分及理由(满分4分)
学生的思路是令 \(x=nT\) 并利用周期函数的积分性质,但证明不完整。在标准答案中,利用(Ⅰ)中构造的有界周期函数 \(F(t)\) 得到 \(\lim_{x\to+\infty}\frac{F(x)}{x}=0\),从而直接推出结论。学生试图用夹逼定理,但夹逼不等式的书写有误(例如“当 \(x \leq nT\) 时”应为考虑 \(nT \leq x < (n+1)T\) 的情形),且夹逼的左右极限计算不严谨。此外,学生未说明 \(f\) 连续且周期,因此积分可加性成立,但证明框架基本正确,主要思路正确但细节有瑕疵。扣 1 分。得 3 分。
(Ⅲ)得分及理由(满分4分)
学生直接写出 \(\lim_{x\to+\infty}\frac{\frac{x}{T}\int_0^T \frac{\sin^2 t}{1+\cos^4 t}dt}{\frac{x}{T}\int_0^T \frac{1}{1+\cos^4 t}dt}\),这隐含了将积分区间按周期分段并取平均的思想,但这里有两个问题:
1. 被积函数 \(\frac{\sin^2 t}{1+\cos^4 t}\) 和 \(\frac{1}{1+\cos^4 t}\) 的周期是 \(\pi\),不是任意 \(T\),学生未指出周期具体值,也未计算积分值。
2. 分母中误写为 \(\cos^4 t\)(应为 \(\cos^2 t\)),这可能是识别错误,但即使按 \(\cos^4 t\) 计算,未给出积分结果,也未完成极限值的计算。
因此,该部分解答不完整,没有最终结果,且关键步骤有误(被积函数写错)。扣 2 分。得 2 分。
题目总分:4+3+2=9分

评分及理由
(Ⅰ)得分及理由(满分6分)
第1次识别结果中,学生正确写出 \( f(x,y) = (x-y)^3 + C(y) \),并由 \( f'_y \) 得到 \( C'(y) = -3y^2 + 6 \),积分得 \( C(y) = -y^3 + 6y + C \),利用 \( f(0,0)=0 \) 得 \( C=0 \),最终得到 \( f(x,y) = (x-y)^3 - y^3 + 6y \)。过程完整,与标准答案一致,应得满分6分。
第2次识别结果中,在计算 \( C'(y) \) 时出现错误:将 \( C'(y) \) 写为 \( -3y^2 + b \)(b未确定),且后续未正确利用条件确定常数,导致表达式不完整。但根据“两次识别只要有一次正确则不扣分”的原则,以第1次识别为准,不扣分。
因此(Ⅰ)部分得6分。
(Ⅱ)得分及理由(满分6分)
第1次识别结果中:
- 求驻点:正确解出 \( (\sqrt{2},\sqrt{2}) \) 和 \( (-\sqrt{2},-\sqrt{2}) \),并指出只有前者在区域内。得1分(此步骤共1分)。
- 边界分析:学生只考虑了边界 \( y=3-x \)(即 \( L_3 \)),并代入得到 \( f(x,3-x) = x^3 - 5x^2 + 9x \),但此表达式化简有误(标准答案为 \( (2x-3)^3 - (3-x)^3 + 6(3-x) \)),导致后续导数、单调性分析均基于错误表达式,属于逻辑错误。此外,完全忽略了边界 \( L_1: x=0 \) 和 \( L_2: y=0 \) 上的分析(标准答案中需分别讨论),遗漏了关键的可能极值点(如 \( (0,1) \)、\( (0,0) \) 等)。此部分应扣分。
- 边界交点:列出了 \( (0,0)、(3,0)、(0,3) \),正确。
- 计算函数值:部分计算错误:
- \( f(\sqrt{2},\sqrt{2}) \) 计算为 \( -2\sqrt{2}+6\sqrt{2}=4\sqrt{2} \) 正确;
- \( f(0,3) \) 计算为 \( -27+27+18=18 \) 错误(正确应为 \( -36 \)),但最后结论中又写最小值为 \( -36 \),前后矛盾;
- \( f(3,0)=27 \) 正确;
- 遗漏了 \( (0,1) \) 和 \( (5/3,4/3) \) 等点的计算。
- 最值结论:虽然结论“最大值为27,最小值为-36”与标准答案一致,但分析过程存在上述严重遗漏和计算错误,不能给满分。
第2次识别结果中:边界分析同样只考虑了 \( y=3-x \),且函数表达式、导数分析均与第1次类似错误;函数值计算中 \( f(0,3) \) 写为-36正确,但 \( f(\sqrt{2},\sqrt{2}) \) 表达式中含未定常数b,逻辑不完整。
综合两次识别,学生在(Ⅱ)部分的主要问题是:边界分析不完整(缺失两条边界的讨论),边界 \( L_3 \) 上的函数表达式化简错误,导致后续分析无效;且函数值计算部分有矛盾。根据评分标准,逻辑错误需扣分。考虑到最终最值结论正确,但过程缺失严重,给予部分分数。
扣分点:驻点求解正确(1分),边界交点正确(1分),最值结论正确(1分)。但边界分析缺失两条边(扣2分),边界 \( L_3 \) 表达式错误及分析错误(扣1分),函数值计算有矛盾(扣1分)。
因此(Ⅱ)部分得3分。
题目总分:6+3=9分
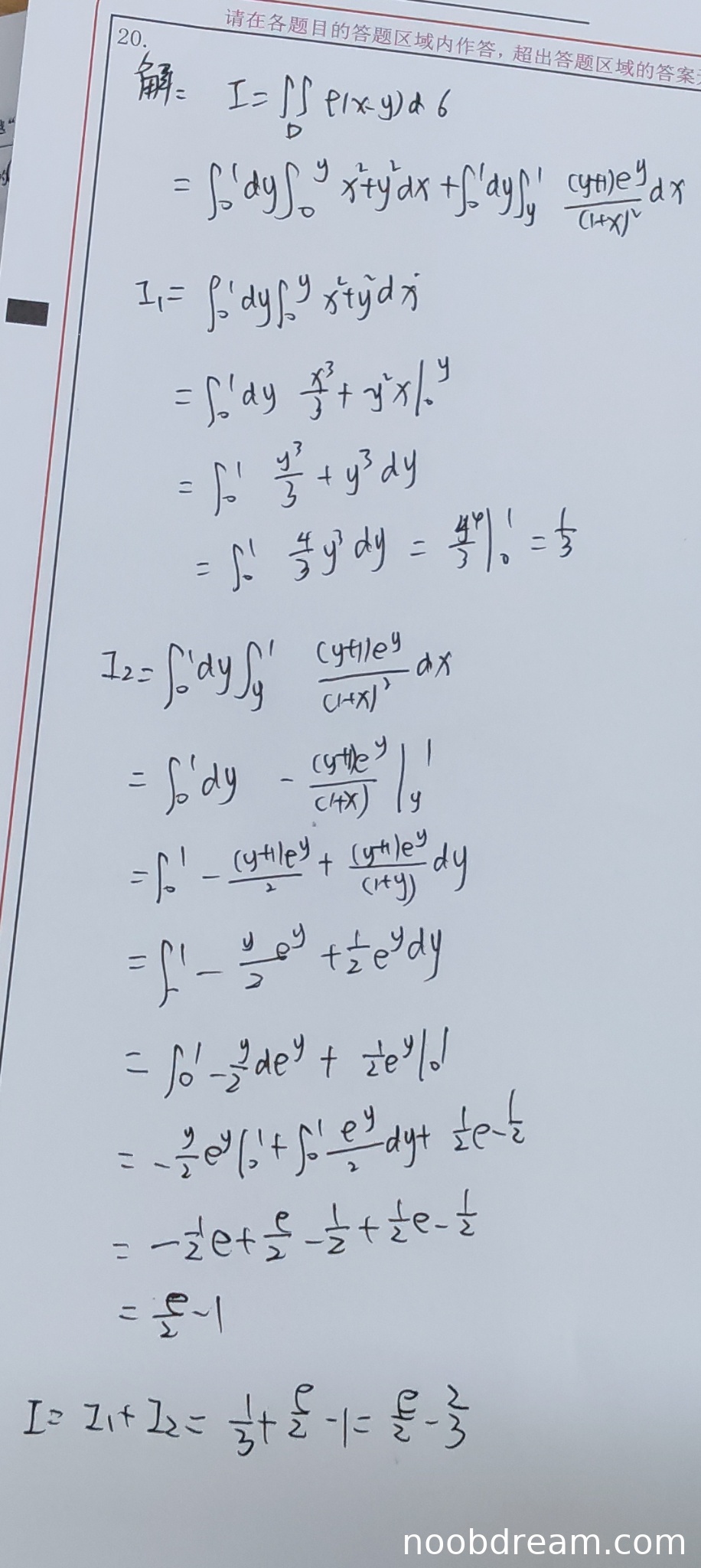
评分及理由
(1)得分及理由(满分12分)
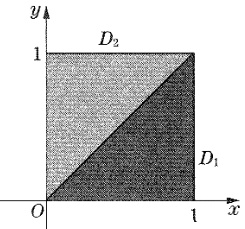
学生作答给出了两次识别结果,但核心内容一致。整体思路正确:将区域D按y=x分割为两部分,分别对应被积函数的不同表达式,然后化为二次积分计算。
具体步骤:
1. 正确写出积分区域的分割方式,并对应正确的被积函数。
2. 计算 \(I_1 = \iint_{D_2} (x^2+y^2)d\sigma\) 时,积分次序选择先x后y(x从0到y,y从0到1),计算过程正确,结果 \(\frac{1}{3}\) 正确。
3. 计算 \(I_2 = \iint_{D_1} \frac{(y+1)e^y}{(1+x)^2}d\sigma\) 时,积分次序选择先x后y(x从y到1,y从0到1)。这里需要注意,学生第一次识别结果中写的是 \(\int_{0}^{1}dy\int_{y}^{1} \frac{(y+1)e^{y}}{(1+x)^{2}}dx\),这对应的是区域 \(D_1\)(即y
尽管第二次识别结果中 \(I_1\) 的积分表达式出现了笔误(写成了 \(\int_{0}^{1}dy\int_{0}^{y}\frac{x^{2}}{x + y}dx\)),但根据上下文(后续计算步骤和结果)可以判断为识别错误,且第一次识别结果中该部分表达式正确。根据“禁止扣分”原则,此类识别错误不扣分。
因此,该解答逻辑清晰,计算正确,应得满分。
得分:12分
题目总分:12分

评分及理由
(Ⅰ)得分及理由(满分6分)
学生只证明了第(Ⅰ)问,但证明过程存在逻辑错误。学生试图利用奇函数性质和积分条件推导出 \( f(a)=0 \),进而得到 \( F(a)=0 \),然后应用罗尔定理。然而,从 \(\int_{-a}^{0} f(x) dx = \frac{1}{2}a^2 f(a)\) 和奇函数性质(\(\int_{-a}^{0} f(x) dx = -\int_{0}^{a} f(x) dx\))确实可以推出 \(\frac{1}{2}a^2 f(a) = -\frac{1}{2}a^2 f(a)\),从而 \(f(a)=0\)。但题目给出的条件是 \(\int_{0}^{a} f(x) dx = \frac{1}{2}a^2 f(a)\),学生将其错误地用于推导 \(\int_{-a}^{0} f(x) dx\),逻辑上不严谨且绕过了题目设定的辅助函数构造和积分中值定理的应用思路。虽然最终得到了 \(f(a)=0\) 和 \(F(a)=0\),并应用罗尔定理得出 \(f'(\xi)=f(a)=0\),这与结论 \(f'(\xi)=f(a)\) 在 \(f(a)=0\) 时形式上一致,但证明方法偏离了标准答案的核心思想(利用积分中值定理和 \(F(x)\) 的零点分布),且关键步骤(从给定积分条件推导 \(f(a)=0\))的推理链条存在跳跃和错误应用(错误地将条件用于对称区间)。因此,不能给满分。考虑到学生正确构造了 \(F(x)\),并试图应用罗尔定理,但主要逻辑推理有缺陷,扣3分。
得分:3分
(Ⅱ)得分及理由(满分6分)
学生没有对第(Ⅱ)问进行任何证明或讨论,因此得0分。
得分:0分
题目总分:3+0=3分

评分及理由
(Ⅰ)得分及理由(满分6分)
学生作答中,第一次识别结果对(Ⅰ)的解答表述混乱,符号识别错误较多(如“r(E)=r(\overline {ii})=r(\overline {iz})”),但最终得到了a=±1的结论。第二次识别结果思路基本正确:通过向量组等价推出秩相等,进而由|A|=0得到a²=1,从而a=±1。虽然矩阵化简过程与标准答案不完全一致,但核心逻辑正确,且最终结论正确。根据“思路正确不扣分”原则,以及考虑到识别可能带来的符号误写(如矩阵元素),本部分不扣分。
得分:6分
(Ⅱ)得分及理由(满分6分)
学生作答存在多处逻辑错误和计算错误:
1. 逻辑错误1(相似的必要条件):在a=1时,学生判断A与B不相似的理由是特征值不同(A: 1,0,2;B: -1,2,0 或 -1,0,0),这与标准答案中利用迹不同判断的思路一致,结论正确。但在a=-1时,学生给出的矩阵A和B的元素均有错误(例如A的(3,1)元素、B的多个元素),这导致后续计算基于错误的矩阵进行。
2. 逻辑错误2(特征值与特征向量计算):基于错误的矩阵A和B计算特征值和特征向量,虽然特征多项式结果碰巧与标准答案一致(特征值为1,-2,0),但求出的特征向量(如λ=1对应(-1,-3,1)^T)与标准答案不同,且未验证是否为对应矩阵的特征向量。
3. 逻辑错误3(矩阵P的求解):学生构造的P1和P2由错误的特征向量组成,且P2的构造直接使用了题目给出的B矩阵(但写错了元素)而非其特征向量,这是概念错误。后续计算P2^{-1}和P的过程也因此错误,最终得到的P=\begin{pmatrix}1&0&0\\0&-1&0\\0&0&1\end{pmatrix}是一个对角阵,这显然不能使A和B相似(除非A=B)。
4. 结论错误:学生最终给出的P不满足P^{-1}AP=B,因此整个(Ⅱ)的解答虽然尝试了相似对角化的方法,但核心步骤(矩阵写错、特征向量求错、P构造错误)存在根本性逻辑错误。
由于(Ⅱ)的解答过程存在严重的逻辑错误,且未得到正确结果,故不能给分。
得分:0分
题目总分:6+0=6分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


