
科目组合
数学二: 高等数学 、线性代数
答题情况分析报告
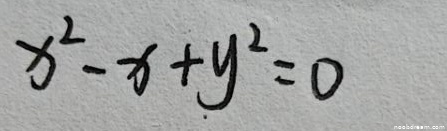
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(x^{2}-x+y^{2}=0\)。将此方程改写为标准形式:\((x^{2}-x) + y^{2} = 0\),配方得 \((x-\frac{1}{2})^{2} + y^{2} - \frac{1}{4} = 0\),即 \((x-\frac{1}{2})^{2}+y^{2}=\frac{1}{4}\)。这与标准答案完全一致。因此,学生答案正确,得5分。
题目总分:5分
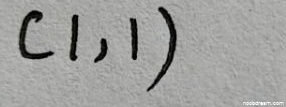
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为“(1,1)”,与标准答案“(1,1)”完全一致。根据题目要求,正确则给5分。因此本题得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(y = \arctan(x + y) - \frac{\pi}{4}\),这与标准答案 \(y=\arctan (x+y)-\frac{\pi}{4}\) 完全一致。
根据题目要求,正确则给5分。虽然答案是以隐函数形式给出,但这是微分方程 \(y'=\frac{1}{(x+y)^{2}}\) 满足 \(y(1)=0\) 的常见且正确的解。因此,本题得分为5分。
题目总分:5分
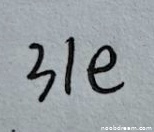
评分及理由
(1)得分及理由(满分5分)
学生作答的两次识别结果均为“31e”,这与标准答案“31e”完全一致。根据评分要求,答案正确则给满分。虽然识别结果中附带了一些说明性文字(如“由于不太明确具体语境...”),但根据规则“对于答案中包含多余的信息错误,是识别问题则不扣分”,这些文字不影响对核心答案“31e”的判断。因此,本题得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(\frac{3}{2}\pi\),这与标准答案 \(k=\frac{3\pi}{2}\) 完全一致。根据题目要求,填空题正确则给满分5分。因此,本题得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为“-1”。标准答案为“-4”。学生的答案与标准答案不符。题目要求向量组线性相关且其中任意两个向量线性无关,这等价于向量组的秩为2。通过分析向量组构成的矩阵的行列式或秩的条件,可以推导出参数a和b需满足的关系,最终得到ab = -4。学生的答案-1不符合推导出的条件,因此答案错误。根据评分规则,本题为填空题,正确得5分,错误得0分。故本题得分为0分。
题目总分:0=0分

评分及理由
(1)得分及理由(满分10分)
本题满分10分。学生的解答过程存在多处逻辑错误和计算错误,具体分析如下:
- 对称性使用错误:学生正确地指出了区域关于直线 \(y = x\) 对称,并写出了 \(\iint_{D}(1 + x - y)dxdy = \iint_{D}(1 + y - x)dxdy\)。这一步是正确的。
- 推导过程错误:学生接下来的推导 \(\iint_{D}(1 + x - y)dxdy = \frac{1}{2} \cdot \iint_{D}[2 + (x + y) - (x + y)]dxdy\) 存在逻辑错误。将两个对称的表达式相加,应为 \(\iint_{D}(1 + x - y)dxdy = \frac{1}{2} \iint_{D}[(1+x-y)+(1+y-x)] dxdy = \frac{1}{2} \iint_{D} 2 dxdy = \iint_{D} dxdy\)。学生的写法中括号内表达式为 \([2 + (x + y) - (x + y)]\),这等价于 \(2\),但前面的系数 \(\frac{1}{2}\) 和等号左边的表达式没有构成正确的等式关系,属于表述混乱。不过,最终他得到了 \(=\iint_{D}dxdy\) 这个关键结论(在第二次识别结果中,他漏写了前面的 \(\frac{1}{2}\),直接得到此结果,但过程跳跃)。鉴于核心结论“原积分等于区域面积”是正确的,且标准答案也利用了此结论,这一步的思路本质正确,但表述不严谨。此处不按逻辑错误扣分,因为最终目标正确。
- 面积计算严重错误:学生计算区域面积 \( \iint_{D} dxdy \) 的方法完全错误。他试图用定积分 \(\int_{0}^{1}3xdx+\int_{1}^{3}\frac{3}{x}dx-\int_{1}^{3}\frac{1}{3}xdx\) 来计算,这显然不是对所述曲线围成区域面积的正确表达。区域由曲线 \(xy=1/3, xy=3\) 和直线 \(y=x/3, y=3x\) 围成,是一个在极坐标或曲线坐标下更方便处理的区域,而不是简单的x型或y型区域。学生所用的积分上下限和表达式没有依据,属于对区域理解的根本性错误,并导致了错误的数值结果 \(\frac{1}{6}+3\ln3\)。
- 最终答案错误:标准答案为 \(\frac{8}{3}\ln3\),而学生答案为 \(\frac{1}{6}+3\ln3\),两者不符。
扣分说明:本题解答的核心步骤“利用对称性化简被积函数”正确,但后续计算区域面积的方法完全错误,导致最终答案错误。这是主要的逻辑与计算错误。由于面积计算是本题的主要计算部分,此错误导致无法得到正确结果。
给予部分分数以肯定其正确的解题思路(对称性应用)。扣除因面积计算完全错误导致的分数。
得分:3分(满分10分)。
题目总分:3分

评分及理由
(1)得分及理由(满分6分)
学生正确应用变换 \( x = e^t \) 将欧拉方程化为常系数线性微分方程,并正确求解得到通解 \( y = C_1 x^3 + C_2 x^{-3} \)。代入初始条件 \( y(1)=2, y'(1)=6 \) 后,正确解出 \( C_1=2, C_2=0 \),从而得到特解 \( y = 2x^3 \)。整个求解过程逻辑清晰,结果正确。虽然第一次识别结果中出现了“q”这样的疑似识别错误字符(应为“9”),但根据上下文和第二次识别结果,可以判断为误写,不影响核心逻辑。因此,本题得满分6分。
(2)得分及理由(满分6分)
学生正确代入 \( y = 2x^3 \),得到积分 \( \int_{1}^{2} 2x^3 \sqrt{4 - x^2} dx \)。并正确选择了三角代换 \( x = 2\sin t \) 进行处理,正确计算了积分上下限的变换(\( x=1 \) 时 \( t=\pi/6 \),\( x=2 \) 时 \( t=\pi/2 \)),并将被积函数正确化简为关于 \( t \) 的表达式。然而,学生的作答在化简过程中出现了错误:从 \( 2 \times (2\sin t)^3 \cdot 2\cos t \cdot 2\cos t dt \) 化简时,系数计算有误,应为 \( 2 \times 8 \sin^3 t \times 2\cos t \times 2\cos t = 64 \sin^3 t \cos^2 t \),但学生后续写成了 \( 64 \int \sin^3 t (1 - \sin^2 t) dt \),这本质上是 \( 64 \int \sin^3 t \cos^2 t dt \) 的等价写法,没有错误。但是,学生的解答在积分化简后并未完成最终的计算,没有得出如标准答案所示的数值结果 \( \frac{22}{5}\sqrt{3} \)。因此,解题过程不完整,扣2分。本题得4分。
题目总分:6+4=10分
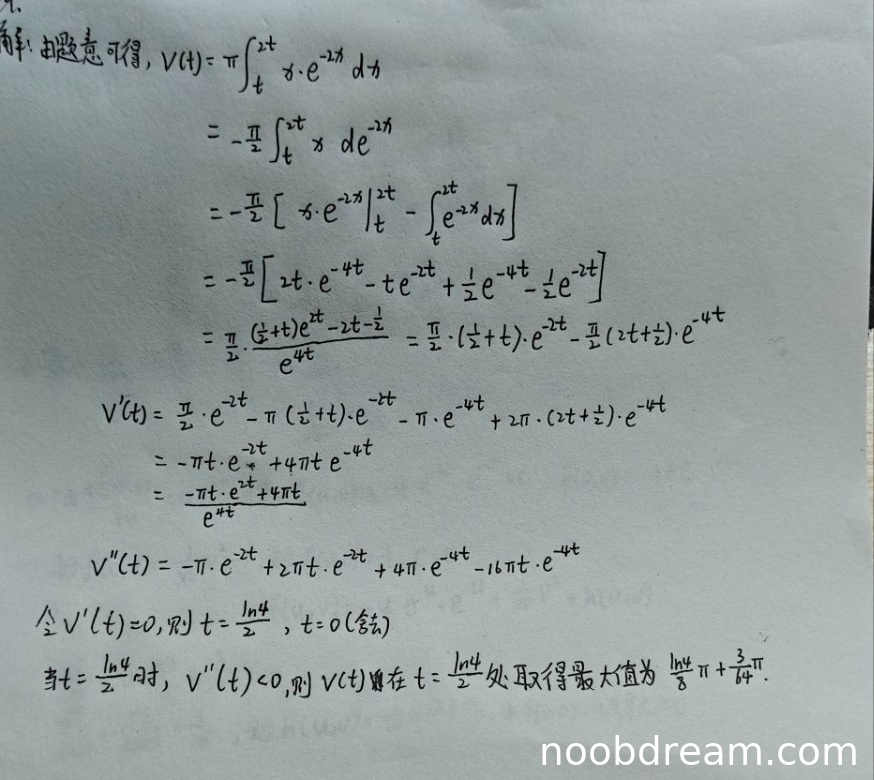
评分及理由
(1)得分及理由(满分12分)
学生作答给出了完整的解题过程:正确写出旋转体体积公式 \( V(t) = \pi \int_t^{2t} x e^{-2x} dx \),使用分部积分法求出 \( V(t) \) 的表达式(尽管化简形式与标准答案不同,但等价),然后对 \( V(t) \) 求导得到 \( V'(t) \),并令 \( V'(t) = 0 \) 解得临界点 \( t = \frac{\ln 4}{2} = \ln 2 \)(学生写为 \( \frac{\ln 4}{2} \),正确),通过二阶导数判断为极大值点,并计算出最大值 \( \frac{\ln 4}{8} \pi + \frac{3}{64} \pi \)。该结果与标准答案 \( \left( \frac{\ln 2}{16} + \frac{3}{64} \right) \pi \) 等价(因为 \( \frac{\ln 4}{8} = \frac{2\ln 2}{8} = \frac{\ln 2}{4} \),注意标准答案为 \( \frac{\ln 2}{16} \),这里学生计算有误,见下文扣分点)。
但存在以下问题:
- 在最终最大值表达式中,学生给出 \( \frac{\ln 4}{8} \pi + \frac{3}{64} \pi \),而标准答案为 \( \left( \frac{\ln 2}{16} + \frac{3}{64} \right) \pi \)。由于 \( \frac{\ln 4}{8} = \frac{2\ln 2}{8} = \frac{\ln 2}{4} \),不等于 \( \frac{\ln 2}{16} \),说明学生在计算定积分 \( V(\ln 2) \) 时出现算术错误。标准答案中 \( V(\ln 2) = \pi \int_{\ln 2}^{2\ln 2} x e^{-2x} dx \) 计算结果为 \( \left( \frac{\ln 2}{16} + \frac{3}{64} \right) \pi \),学生未展示该积分计算过程,直接给出错误系数,属于计算错误。
- 学生在求导过程中表达式较繁琐,但最终导函数化简为 \( V'(t) = -\pi t e^{-2t} + 4\pi t e^{-4t} = \pi t e^{-2t}(4e^{-2t} - 1) \),与标准答案一致(尽管学生写为 \( \frac{-\pi t e^{2t} + 4\pi t}{e^{4t}} \),但等价)。此处不扣分。
根据评分要求,思路正确不扣分,但最终答案计算错误应扣分。本题满分12分,由于核心步骤正确,仅最终数值结果错误,扣2分。
得分:10分。
题目总分:10分

评分及理由
(1)得分及理由(满分6分)
学生作答中,第一次识别结果在计算二阶偏导数时出现了明显的符号错误和展开错误,例如 \(\frac{\partial^2 g}{\partial x^2}\) 的表达式不正确,但最终通过代入方程化简得到了正确结果 \(\frac{\partial^2 f}{\partial u\partial v} = \frac{1}{25}\)。第二次识别结果中,复合函数设定有误(写成了 \(g(x,y)=f(2x + 3y,x - y)\)),但后续偏导计算和化简过程逻辑正确,且最终结果正确。根据“禁止扣分”原则,识别中的字符误写(如“s”代替“x”)和复合函数设定笔误不扣分,且核心逻辑(求偏导、代入方程、化简得结果)正确。因此,第(1)问得满分6分。
(2)得分及理由(满分6分)
学生作答中,利用已知条件 \(\frac{\partial f(u,0)}{\partial u} = ue^{-u}\) 积分得到 \(f(u,0) = -ue^{-u} - e^{-u} + C\),并结合 \(f(0,v)\) 确定常数,思路正确。在求解 \(f(u,v)\) 表达式时,通过设 \(f(u,v) = -ue^{-u} - e^{-u} + \frac{1}{50}v^2 + h(u,v)\),并利用 \(\frac{\partial^2 f}{\partial u\partial v} = \frac{1}{25}\) 求解 \(h(u,v)\),最终得到正确表达式 \(f(u,v) = -ue^{-u} - e^{-u} + \frac{1}{50}v^2 + \frac{1}{25}uv\)。虽然过程中对 \(h(u,v)\) 的积分常数处理略有跳跃,但整体逻辑与标准答案等价,且结果正确。因此,第(2)问得满分6分。
题目总分:6+6=12分
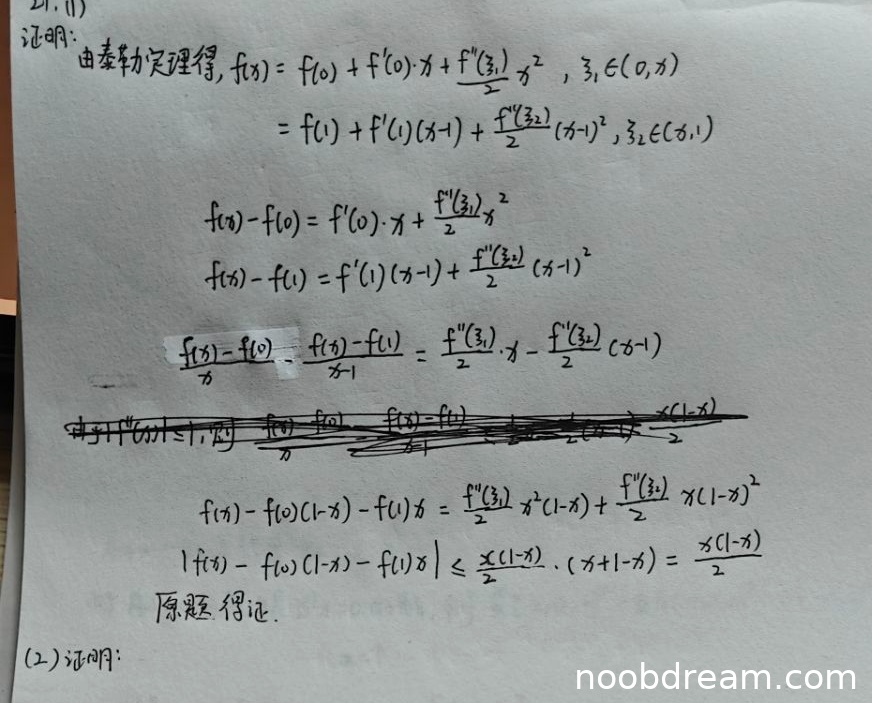
评分及理由
(1)得分及理由(满分6分)
学生尝试使用泰勒公式进行证明,思路与标准答案不同但方向正确。然而,在推导过程中存在多处逻辑错误和跳跃:
- 从两个泰勒展开式出发,得到 \(f(x)-f(0)=f'(0)x+\frac{f''(\xi_1)}{2}x^2\) 和 \(f(x)-f(1)=f'(1)(x-1)+\frac{f''(\xi_2)}{2}(x-1)^2\) 是正确的。
- 但后续构造 \(\frac{f(x)-f(0)}{x}-\frac{f(x)-f(1)}{x-1}\) 并声称它等于 \(\frac{f''(\xi_1)}{2}x-\frac{f''(\xi_2)}{2}(x-1)\) 是错误的。实际上,由两个泰勒式分别除以 \(x\) 和 \(x-1\) 后相减,会得到: \[ \frac{f(x)-f(0)}{x} = f'(0)+\frac{f''(\xi_1)}{2}x,\quad \frac{f(x)-f(1)}{x-1}=f'(1)+\frac{f''(\xi_2)}{2}(x-1) \] 相减后应为: \[ \frac{f(x)-f(0)}{x}-\frac{f(x)-f(1)}{x-1}=[f'(0)-f'(1)]+\frac{f''(\xi_1)}{2}x-\frac{f''(\xi_2)}{2}(x-1) \] 学生忽略了 \(f'(0)-f'(1)\) 项(已知 \(f'(0)=f'(1)\),所以该项为0,但推导中未说明直接舍去,逻辑不完整)。
- 接着,学生直接写出 \(f(x)-f(0)(1-x)-f(1)x=\frac{f''(\xi_1)}{2}x^2(1-x)+\frac{f''(\xi_2)}{2}x(1-x)^2\),这一步缺乏推导过程,是凭空出现的,与前面的式子没有直接代数关系,属于逻辑断裂。
- 最后利用 \(|f''|\le 1\) 得到不等式,虽然形式正确,但中间推导不严谨,关键等式未建立。
由于证明的核心步骤存在严重逻辑错误,不能给满分。考虑到学生知道使用泰勒公式并试图利用二阶导有界,有一定思路,但执行错误较多,扣分较多。给分:2分。
(2)得分及理由(满分6分)
学生只写了“(2)证明:”后无内容,没有给出第二部分证明。因此本题未作答,得0分。
题目总分:2+0=2分

评分及理由
(1)得分及理由(满分6分)
学生作答中,第一问的最终答案 a=1, b=2 是正确的。但解题过程存在多处逻辑错误和表述不严谨之处,需要扣分。
扣分点:
1. 由“方程组\(Ax = 0\)的解是\(B^Tx = 0\)的解,但两个方程组不同解”并不能直接推出“\(r(A)\neq r(B)\)”。实际上,\(B\)是3×2矩阵,\(B^T\)是2×3矩阵,秩的比较对象不直接。此处推理逻辑有误。
2. 学生直接断言“已知\(r(A)=2\)”,但并未给出计算或说明理由。在标准答案中,这是通过分析增广矩阵的秩推导出来的。此处属于关键步骤缺失。
3. 在计算\(B\)时,第一次识别结果中写成了\(B=\begin{bmatrix}1&1&1\\2&2&2\end{bmatrix}\),这明显是错误的(维度不对),但第二次识别结果正确。根据“禁止扣分”原则第3条,以正确的一次为准,不扣分。
4. 在利用通解建立关系时,逻辑表述混乱。学生试图说明\(Ax=0\)的解向量可以由\(B^Tx=0\)的基础解系线性表示,但写法“\(m(-2,0,1)^{T}+n(-1,1,0)^{T}=(-1,-a,1)^{T}\)”意味着存在一组确定的\(m, n\)使等式成立,这并不准确。更严谨的说法是\((-1,-a,1)^T\)与\((-2,0,1)^T\)和\((-1,1,0)^T\)线性相关。虽然最终得到了正确的a=1,但推理过程不严谨。
鉴于最终答案正确,但核心推理过程存在逻辑错误和关键步骤缺失,扣3分。
得分:6 - 3 = 3分。
(2)得分及理由(满分6分)
学生作答中,第二问的最终标准形(6y3^2)和特征值(0,0,6)是正确的,并正确求出了对应的特征向量。但正交变换矩阵\(Q\)未完整求出,过程存在严重错误。
扣分点:
1. 致命错误:在将特征向量正交化时,得出“\(\beta_2 = 0\)”。这是严重的计算或逻辑错误。零向量不能作为特征向量,也无法构成正交矩阵的列。这表明学生未能正确完成施密特正交化过程,导致最终的正交变换矩阵缺失。
2. 由于上述错误,学生没有给出最终的正交矩阵\(Q\),也没有写出完整的正交变换\(x=Qy\)。题目要求“求正交矩阵\(x = Qy\)将\(f\)化为标准形”,这是一个完整的任务,学生只完成了一半(求出了特征值和未正交化的特征向量)。
鉴于特征值和特征向量求对,但正交化过程完全错误,且未给出最终要求的正交矩阵和变换,扣4分。
得分:6 - 4 = 2分。
题目总分:3+2=5分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


