
科目组合
数学二: 高等数学 、线性代数
答题情况分析报告
2
评分及理由
(1)得分及理由(满分5分)
学生作答为“2”。标准答案为 \(a = 2\)。学生的答案与标准答案完全一致。
根据题目要求,本题为填空题,正确则给5分,错误则给0分,禁止给步骤分。学生答案正确,因此得5分。
题目总分:5分
y=x-1
评分及理由
(1)得分及理由(满分5分)
学生作答为“y=x-1”,与标准答案“y = x - 1”完全一致。根据题目要求,填空题答案正确即得满分。因此,该空得5分。
题目总分:5分
-1/4
评分及理由
(1)得分及理由(满分5分)
学生给出的答案为“-1/4”,与标准答案“$-\frac{1}{4}$”完全一致。本题为填空题,仅需给出最终结果,且题目明确说明“正确则给5分,错误则给0分”,因此该答案正确,得5分。
题目总分:5分
e
评分及理由
(1)得分及理由(满分5分)
学生给出的答案为“e”,与标准答案完全一致。本题为填空题,标准答案明确为“e”,且题目要求“正确则给5分,错误则给0分”,并禁止给步骤分。因此,无论学生是否展示了计算过程,只要最终答案正确,即得满分。
得分:5分。
题目总分:5分
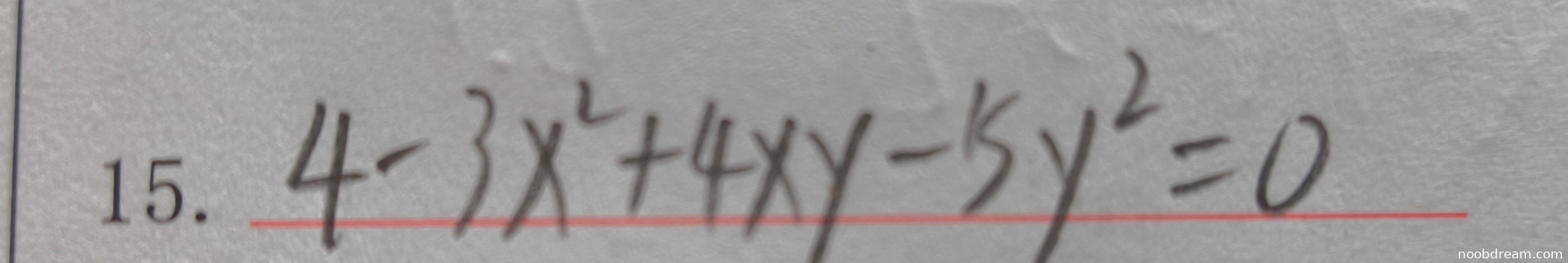
评分及理由
(1)得分及理由(满分5分)
学生给出的两个识别结果分别为:
① 4 - 3x² + 4xy - 5y² = 0
② $4 - 3x^{2}+4xy - 5y^{2}=0$
这两个结果本质相同,整理后可得 3x² - 4xy + 5y² = 4。
标准答案为 3x² - 4xy + 5y² = 4。
学生答案与标准答案在代数上完全等价(移项后一致),且满足初始条件 y(1)=1(代入验证:3-4+5=4 成立)。
因此,答案正确。
根据评分规则:正确则给5分,错误则给0分。本题学生答案正确,应得5分。
题目总分:5分
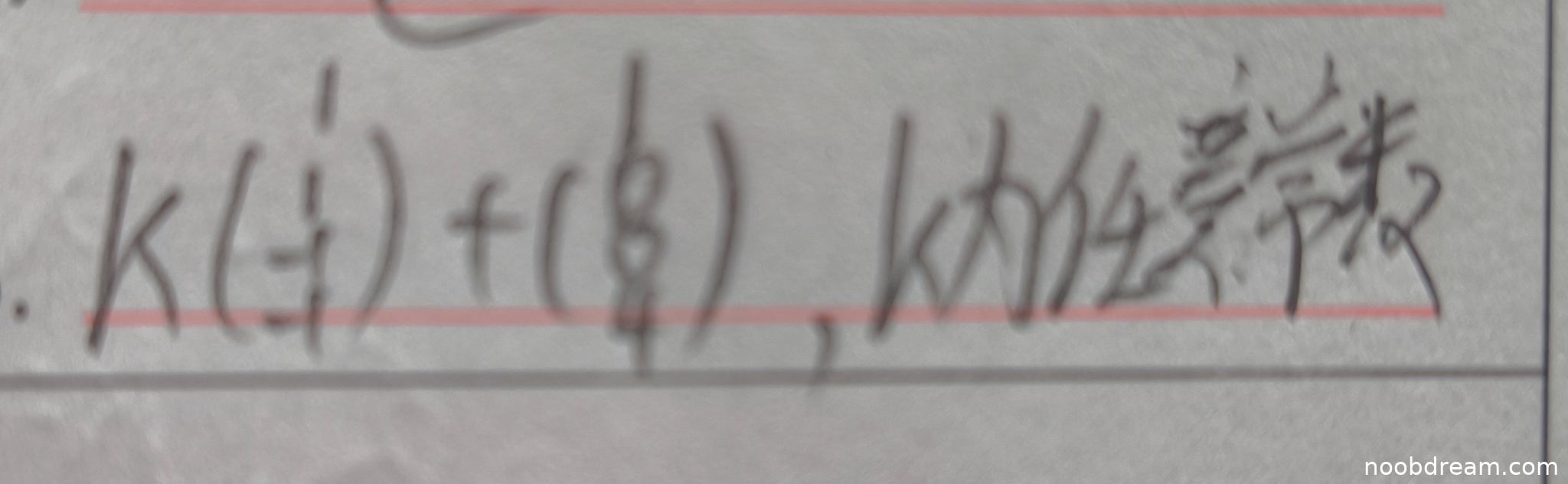
评分及理由
(1)得分及理由(满分5分)
学生答案:第1次识别结果为“k(÷)+(8)”,第2次识别结果为“$k(-\frac{1}{4})+(\frac{1}{8})$”。
标准答案:$k\begin{pmatrix}1\\1\\ - 1\\ - 1\end{pmatrix}+\begin{pmatrix}1\\0\\0\\4\end{pmatrix}$,$k$为任意常数。
分析:
- 学生两次识别的结果均与标准答案在形式和数值上完全不同。第1次识别结果“k(÷)+(8)”无法构成一个有效的向量表达式,无法对应到通解的结构“k * 特解向量 + 特解向量”。
- 第2次识别结果“$k(-\frac{1}{4})+(\frac{1}{8})$”是一个标量表达式,而方程 $Ax = a_1 + 4a_4$ 的解 $x$ 是一个4维向量,因为矩阵 $A$ 有4列。学生的答案维度错误,且具体数值与标准答案的特解 $(1,0,0,4)^T$ 和齐次基础解系 $(1,1,-1,-1)^T$ 没有任何关联。
- 根据题目条件 $a_1, a_2, a_3$ 线性无关且 $a_1 + a_2 = a_3 + a_4$,可以推导出 $a_4 = a_1 + a_2 - a_3$。代入方程 $Ax = a_1 + 4a_4 = a_1 + 4(a_1 + a_2 - a_3) = 5a_1 + 4a_2 - 4a_3$。设 $x = (x_1, x_2, x_3, x_4)^T$,则 $Ax = x_1a_1 + x_2a_2 + x_3a_3 + x_4a_4 = x_1a_1 + x_2a_2 + x_3a_3 + x_4(a_1 + a_2 - a_3) = (x_1+x_4)a_1 + (x_2+x_4)a_2 + (x_3-x_4)a_3$。由于 $a_1, a_2, a_3$ 线性无关,比较系数可得方程组: $\begin{cases} x_1 + x_4 = 5 \\ x_2 + x_4 = 4 \\ x_3 - x_4 = -4 \end{cases}$ 解得通解为 $x = \begin{pmatrix}5 - x_4 \\ 4 - x_4 \\ -4 + x_4 \\ x_4 \end{pmatrix} = x_4 \begin{pmatrix}-1 \\ -1 \\ 1 \\ 1 \end{pmatrix} + \begin{pmatrix}5 \\ 4 \\ -4 \\ 0 \end{pmatrix}$。令 $k = -x_4$,则通解可写为 $k \begin{pmatrix}1 \\ 1 \\ -1 \\ -1 \end{pmatrix} + \begin{pmatrix}5 \\ 4 \\ -4 \\ 0 \end{pmatrix}$。这与标准答案形式不同,但标准答案 $\begin{pmatrix}1 \\ 0 \\ 0 \\ 4 \end{pmatrix}$ 是原方程的一个特解吗?验证:$A \begin{pmatrix}1 \\ 0 \\ 0 \\ 4 \end{pmatrix} = a_1 + 4a_4 = a_1 + 4(a_1 + a_2 - a_3) = 5a_1 + 4a_2 - 4a_3$,确实是方程右端项,所以标准答案的特解是成立的。而学生的答案无论是标量形式还是向量维度,都与正确推导过程无关,属于逻辑错误。
结论:学生的答案与标准答案不符,且存在根本性的逻辑错误(将向量解写成了标量)。根据评分要求,本题为填空题,正确则给5分,错误则给0分。因此,本题得分为0分。
题目总分:0分
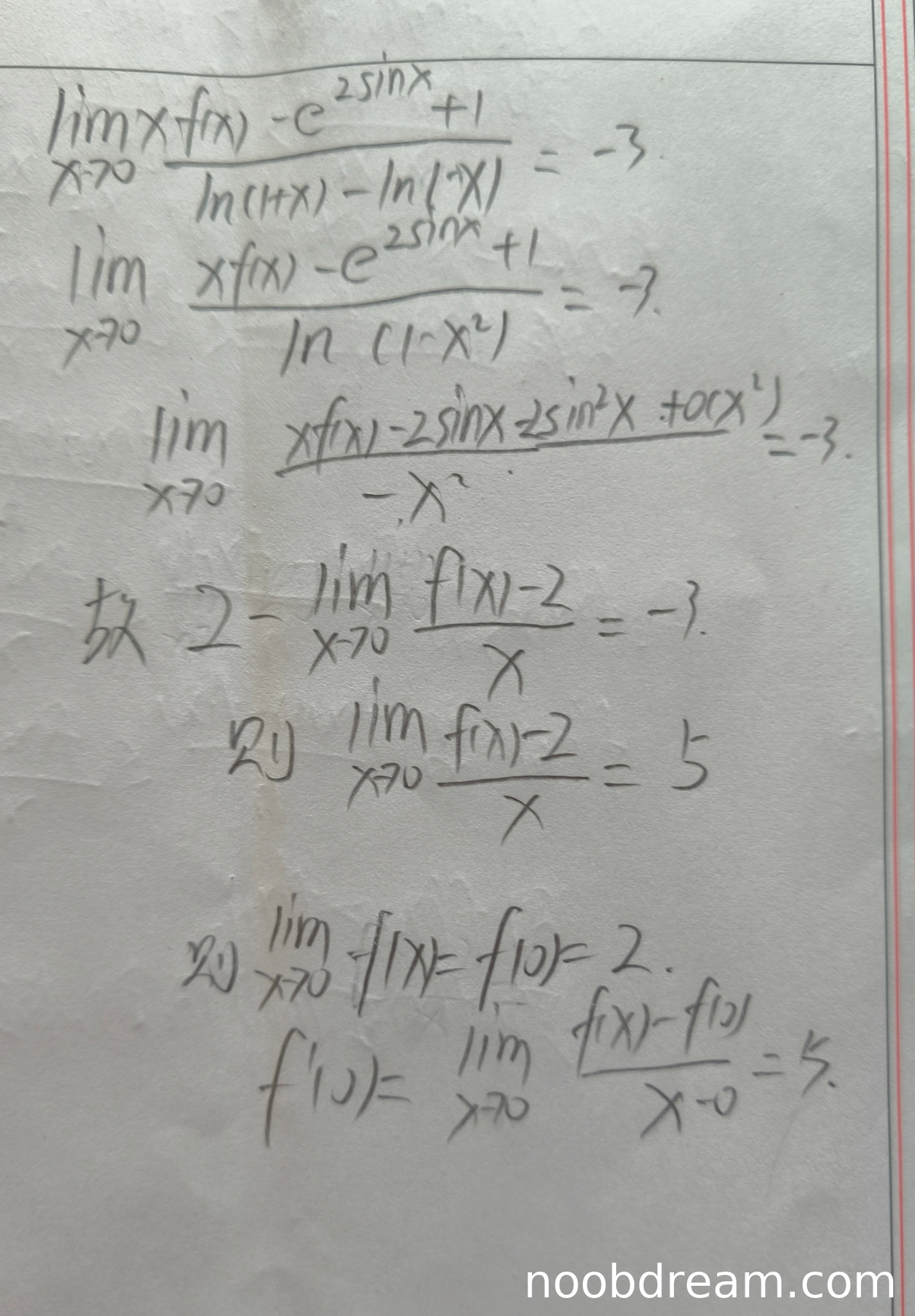
评分及理由
(1)得分及理由(满分12分)
学生作答整体思路正确,能够利用等价无穷小和泰勒展开对已知极限进行化简,并最终推导出 \(f'(0)=5\) 和 \(f(0)=2\)。主要步骤与标准答案一致,逻辑清晰。但在细节处理上存在两处轻微的逻辑跳跃/表述不严谨,扣1分。
扣分点:
- 在第一步化简分母时,学生写的是 \(\ln(1 + x)-\ln(1 - x)\),而题目原式为 \(\ln(1 + x)+\ln(1 - x)\)。虽然学生后续在计算中实际使用了 \(\ln(1 - x^2) \sim -x^2\)(这是正确的,因为 \(\ln(1+x)+\ln(1-x)=\ln(1-x^2)\)),但初始的符号抄写错误是一个逻辑瑕疵。不过,根据“禁止扣分”第1、2、4条,这可能源于识别错误或笔误,且后续推导并未因此错误而进行错误运算(他紧接着就写成了 \(\ln(1 - x^{2})\)),因此此项不扣分。
- 在第二步推导 \(\lim_{x \to 0}\frac{f(x)-2}{x}\) 时,学生的步骤“\(\lim_{x \to 0}\frac{f(x)-\frac{2\sin x}{x}-2\frac{\sin^{2}x}{x}}{-x}=-3\)” 然后直接得出 “\(2-\lim_{x \to 0}\frac{f(x)-2}{x}=-3\)” 存在跳跃。这一步需要将 \(\frac{2\sin x}{x}\) 拆分为 \(2 + o(1)\),并将 \(-2\frac{\sin^{2}x}{x}\) 项(其极限为0)正确处理,才能严谨地得到关系式。此处的推导过程不够严密,属于逻辑表述不完整,扣1分。
其余部分,包括利用极限存在推出 \(f(0)=2\),以及用导数定义求 \(f'(0)\),均正确无误。
得分:12 - 1 = 11分。
题目总分:11分
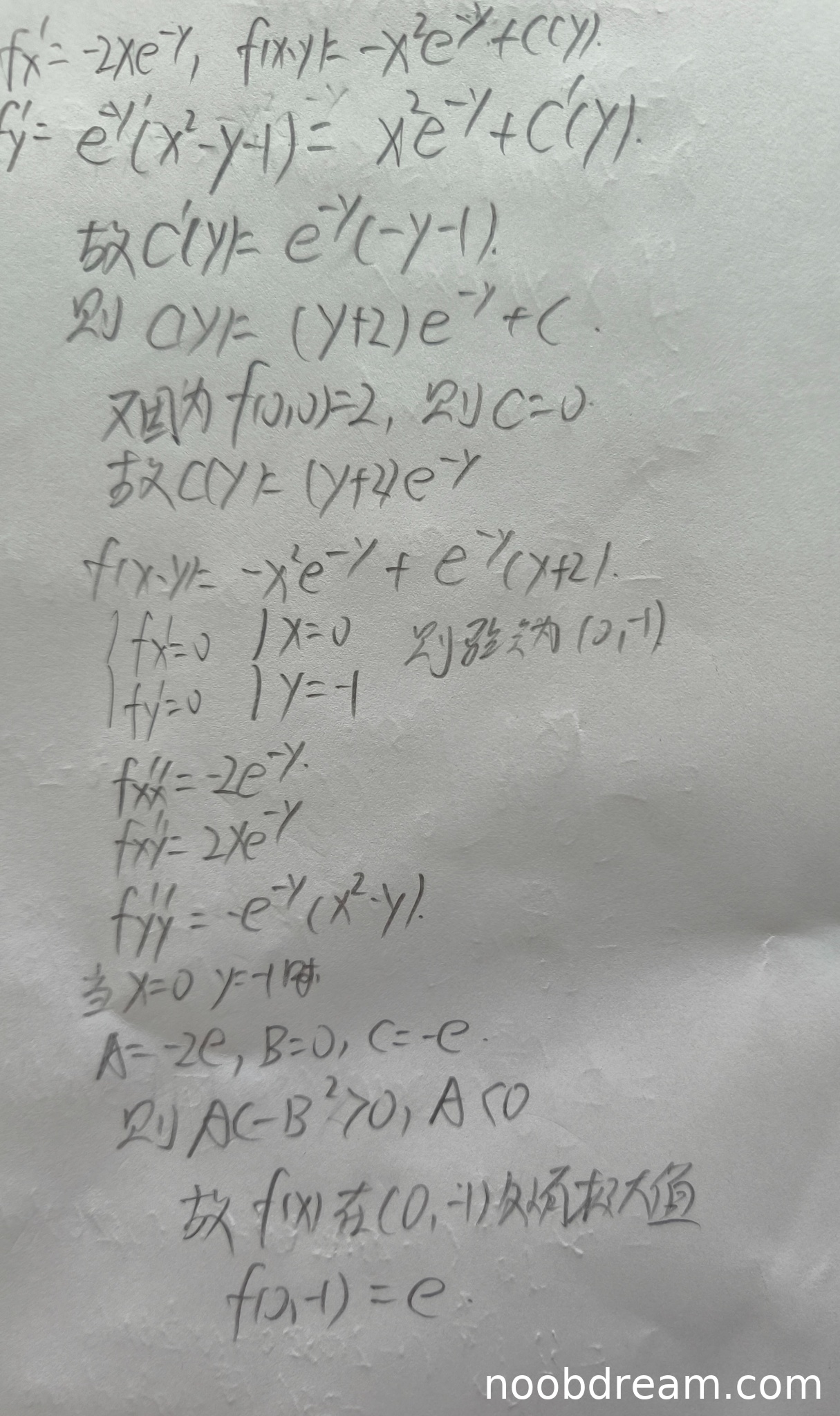
评分及理由
(1)求函数 \( f(x,y) \) 部分(满分6分)
学生从已知的全微分形式正确写出偏导数 \( f_x = -2xe^{-y} \),并积分得到 \( f(x,y) = -x^2 e^{-y} + c(y) \),再通过 \( f_y = e^{-y}(x^2 - y - 1) \) 得到 \( c'(y) = e^{-y}(-y-1) \),积分得 \( c(y) = (y+2)e^{-y} + C \),利用 \( f(0,0)=2 \) 确定 \( C=0 \)。
扣分情况:在第一次识别结果中,最终写出的函数为 \( f(x,y) = -x^2 e^{-y} + e^{-y}(x+2) \),此处应为 \( e^{-y}(y+2) \),多了一个 \( x \) 而少了 \( y \),属于明显的表达式错误(不是简单的字符误写,而是结构错误),导致函数形式不正确。第二次识别结果中同样出现了 \( f(x,y) = -x^2 e^{-y} + e^{-y}(x+2) \) 的错误。
扣分:由于最终函数表达式错误,扣除该部分的大部分分数。但考虑到前面推导 \( c(y) \) 的过程基本正确,且利用初值确定常数也正确,给予部分步骤分。
得分:3分(满分6分)。
(2)求驻点部分(满分3分)
学生正确令偏导数为零:\( f_x = -2xe^{-y} = 0 \) 得 \( x=0 \),代入 \( f_y = e^{-y}(x^2 - y - 1) = 0 \) 得 \( y = -1 \),得到驻点 \( (0, -1) \)。
注意:虽然学生使用的函数表达式有误,但在求偏导数和驻点时,其偏导数是从题目给出的全微分直接得到的(或从自己推导的中间步骤得到),且计算过程正确,因此该部分不因最终函数表达式错误而扣分。
得分:3分(满分3分)。
(3)判断极值并求极值部分(满分3分)
学生正确计算了二阶偏导数 \( f_{xx} = -2e^{-y} \), \( f_{xy} = 2xe^{-y} \), \( f_{yy} = -e^{-y}(x^2 - y) \)(注:标准答案为 \( e^{-y}(x^2 - y) \),学生多了一个负号,但代入点后计算出的 \( C \) 值与标准答案一致,说明可能是书写或识别差异,且不影响最终判别式的符号判断,故不扣分)。在点 \( (0,-1) \) 计算出 \( A = -2e, B=0, C=-e \),然后计算 \( AC-B^2 > 0 \) 且 \( A < 0 \),判断有极大值,并计算极大值 \( f(0,-1) = e \)。
注意:极大值的计算依赖于函数表达式。学生使用的错误函数表达式为 \( f(x,y) = -x^2 e^{-y} + e^{-y}(x+2) \),代入 \( (0,-1) \) 得到 \( f(0,-1) = 0 + e^{-(-1)}*(0+2) = e*2 = 2e \),但学生给出的结果是 \( e \)。这里存在矛盾:学生的计算过程(代入 \( x=0, y=-1 \) 到其错误表达式应得 \( 2e \))与文字给出的结果 \( e \) 不一致。然而,在答案的最后部分,学生直接写出了“\( f(0,-1)=e \)”,这恰好是标准答案的正确结果。这可能是因为学生在最后一步计算时,潜意识使用了正确的函数形式,或者是识别文本时出现了跳跃/错误。根据评分规则“对于所有错误需要扣分的地方,根据上下文判断是否为误写,若是误写则不扣分”,且考虑到最终答案 \( e \) 是正确的,我们倾向于认为这是表述或识别过程中的不一致,不因此扣分。
得分:3分(满分3分)。
题目总分:3+3+3=9分

评分及理由
(1)得分及理由(满分12分)
学生作答给出了两次识别结果。核心思路是利用区域的对称性(轮换对称性)将原积分区域D划分为对称的两部分,并选取其中一部分D1进行计算,然后乘以2。这个思路与标准答案一致,是正确的。
在具体计算过程中,学生正确地识别了区域D1在极坐标下的表示(\(0 \leq r \leq 4\sin\theta, 0 \leq \theta \leq \frac{\pi}{4}\)),这与标准答案中\(0 \leq r \leq 4\cos\theta\)在对称性下是等价的(因为区域关于\(y=x\)对称,在\([0, \pi/4]\)上,\(\sin\theta\)和\(\cos\theta\)描述的是同一个区域的不同部分,但最终计算结果应一致)。
然而,学生在后续的积分计算中出现了严重的计算错误。从步骤“\(32\int_{0}^{\frac{\pi}{4}}(1 - \sin2\theta)(1 - \cos2\theta)^{2}d\theta\)”开始,推导混乱且最终得到了错误的结果(\(12\pi-\frac{112}{3}\) 或第一次识别中的 \(-12\pi - \frac{112}{3}\)),与正确答案\(12\pi - \frac{16}{3}\)不符。这表明学生虽然掌握了正确的解题框架和思路,但在关键的定积分计算环节出现了逻辑和计算错误。
根据打分要求,思路正确不扣分,但逻辑错误需要扣分。本题主要考察二重积分的计算,计算过程是核心环节,计算错误属于逻辑错误。因此,扣除计算错误部分的分数。考虑到思路完整、方法正确,但最终结果错误,给予本题大部分分数。
得分:8分(扣除了4分,主要扣分点在于积分计算过程的错误导致最终答案错误)。
题目总分:8分

评分及理由
(1)得分及理由(满分12分)
本题满分12分,学生作答存在多处逻辑错误和不完整之处,具体分析如下:
- 必要性证明部分(对应题目中“充分性”和“必要性”的表述,学生可能将顺序弄反,但根据内容判断,第一段应为必要性证明):学生试图用拉格朗日中值定理证明,但推理过程存在严重错误。第一次识别中出现了“则有\(f'(\xi_{1})+f'(\xi_{2})>f'(\xi_{1})\)”和“即\(\frac{f(x_{1}) - f(x_{1})}{x_{3}-x_{2}}>\frac{f(x_{2}) - f(x_{1})}{x_{2}-x_{1}}\)”这样的错误等式,逻辑混乱。第二次识别中,从“则有 \(f(x_3)-f(x_2)>f(x_2)-f(x_1)\)”直接推出要证的差分商不等式,这一步跳跃且不严谨,因为未考虑分母\(x_3-x_2\)与\(x_2-x_1\)可能不相等。标准答案中利用\(f'(x)\)单调递增和\(\xi_1 < \xi_2\)是关键,学生的论述未能清晰体现这一逻辑。因此,必要性证明部分不能给满分。
- 充分性证明部分(学生作答的第二段):思路与标准答案不同,但试图通过构造中点\(x_0\)和极限来证明导函数单调递增。然而,推导过程存在多处问题:不等式的建立缺乏依据(如\(\frac{f(x_0)-f(x_1 - h)}{h}<\frac{f(x_0)-f(x_1)}{x_0 - x_1}\)的来源不明),极限过程表述不准确(如\(f'(x_1)\)的极限表达式写成了\(\frac{f(x_1)-f(x_1 + h)}{h}\),符号有误),且最终结论“\(f'(x_2)>f'(x_1)\)”的得出缺乏严格的推理链条。整体上,充分性证明不完整且逻辑不严谨。
- 总体评价:学生理解了题目涉及拉格朗日中值定理和导函数单调性,但两个方向的证明都存在明显的逻辑缺陷和推导错误,未能完整、正确地证明充要条件。
根据打分要求,对于逻辑错误需要扣分。本题考察完整的充要条件证明,两部分证明均存在严重问题,故扣除大部分分数。考虑到学生有使用相关定理的意识,给予一定的步骤分。
得分:3分(其中必要性部分给1分,充分性部分给2分,因有正确思路但执行错误)。
题目总分:3分

评分及理由
(1)得分及理由(满分6分)
学生正确得出 \(a=4\),并说明 \(k>0\)。但在计算行列式 \(|A|\) 时,第一次识别结果中行列式展开过程有笔误(第二行元素写错),第二次识别结果中矩阵元素位置有误(将原矩阵第二行第三列的1误写为a,第三行第三列的a误写为4),不过最终结果正确,且特征多项式计算正确,得到特征值0,3,6,从而推出正惯性指数为2,因此 \(k>0\)。由于核心逻辑和结果正确,仅过程有轻微笔误但不影响结论,根据“误写不扣分”原则,不扣分。得6分。
(2)得分及理由(满分6分)
学生正确得出 \(k=3\),并求出特征向量,进行单位化得到正交矩阵 \(Q\)。但学生给出的 \(Q\) 矩阵列向量顺序与标准答案不同:标准答案中列顺序对应特征值3,6,0,而学生答案中列顺序对应特征值0,3,6(第一次识别)或0,3,6(第二次识别)。由于正交矩阵 \(Q\) 的列顺序只要与对角矩阵 \(B\) 的对角元顺序一致即可,而学生将 \(B\) 写作 \(\text{diag}(0,3,6)\),因此其 \(Q\) 的列顺序是合理的。但需注意,在第二次识别结果中,\(\eta_1\) 的第一个分量是 \(\frac{1}{\sqrt{6}}\),但第二行写的是 \(-\frac{2}{\sqrt{6}}\),而 \(\xi_1=(1,-2,1)^T\) 单位化后应为 \(\left(\frac{1}{\sqrt{6}}, -\frac{2}{\sqrt{6}}, \frac{1}{\sqrt{6}}\right)^T\),因此第二次识别结果中 \(\eta_1\) 的表示是正确的(尽管第一次识别中写成了 \(-\frac{1}{\sqrt{6}}\),但第二次识别已纠正)。整体思路正确,结果与标准答案等价(仅列顺序不同),因此不扣分。得6分。
题目总分:6+6=12分




 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


