
科目组合
数学一: 高等数学 、线性代数 、概率论
答题情况分析报告

评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(\frac{\pi}{4}\),与标准答案完全一致。根据题目要求,正确则给5分。因此,本题得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(\frac{2}{3}\),与标准答案完全一致。根据打分要求,答案正确应给满分。识别结果清晰,无逻辑错误或误写迹象。因此,本题得5分。
题目总分:5分
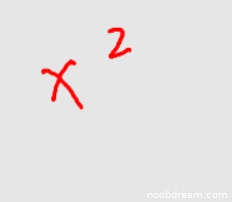
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \( x^{2} \),与标准答案 \( x^{2} \) 完全一致。该答案满足欧拉方程 \( x^{2}y'' + xy' - 4y = 0 \) 以及初始条件 \( y(1) = 1 \),\( y'(1) = 2 \)。因此,本题答案正确,得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为“4π”,与标准答案“4π”完全一致。根据题目要求,填空题正确则给5分。识别结果清晰无误,不存在需要扣分的逻辑错误或误写情况。因此,本题得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(\frac{3}{2}\),与标准答案完全一致。根据题目条件,A的每行元素之和为2,即A的列向量(1,1,1)^T是特征值2对应的特征向量,因此有A*(1,1,1)^T = (2,2,2)^T。而A的伴随矩阵A*满足A*A = |A|I,所以A*(1,1,1)^T = (A_{11}+A_{21}+A_{31}, A_{12}+A_{22}+A_{32}, A_{13}+A_{23}+A_{33})^T。同时,由A*(1,1,1)^T = (2,2,2)^T,可得A*的每行元素之和为2|A|/2? 更直接地,利用公式A* = |A|A^{-1},可得A*(1,1,1)^T = |A|A^{-1}(1,1,1)^T = |A|*(1/2,1/2,1/2)^T = (3/2, 3/2, 3/2)^T,因此A_{11}+A_{21}+A_{31} = 3/2。学生答案正确,逻辑无误,得5分。
题目总分:5分
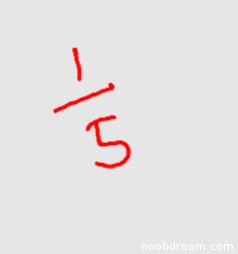
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(\frac{1}{5}\),与标准答案完全一致。根据题目要求,本题为填空题,答案正确即得满分。因此,该小题得5分。
题目总分:5分


评分及理由
(1)得分及理由(满分10分)
学生作答提供了两种识别结果,其中第二次识别给出了完整的解题过程。该过程思路正确:先通分,再利用等价无穷小替换化简分母,然后两次应用洛必达法则,最后代入极限值计算得到结果1/2。此方法与标准答案中的方法一(通分后使用洛必达法则)在核心思路上一致,且计算过程逻辑清晰、步骤完整,最终答案正确。
第一次识别结果仅为片段,但根据上下文判断,可能是识别不全,且第二次识别已给出完整正确解答,因此不影响评分。
根据打分要求,思路正确且答案正确应给满分。故本题得分为10分。
题目总分:10分


评分及理由
(1)收敛域部分(满分6分)
得分:5分
理由:学生正确地将级数拆分为两个级数之和,并分别求出了各自的收敛域。对于 \(S_1(x)\),正确得出收敛域为 \(x>0\);对于 \(S_2(x)\),正确计算收敛半径为1,并判断了端点 \(x=\pm 1\) 处的收敛性,得出收敛域为 \([-1,1]\)。综合两部分收敛域时,学生得出原级数的收敛域为 \((0,1]\),这是正确的。但在 \(S_1(x)\) 的收敛域表述中,学生写的是“收敛域为 \((0,+\infty)\)”,而标准答案中通过比值法得到 \(x>0\) 时收敛,两者本质一致,但学生未明确指出 \(x=0\) 时发散(因为 \(e^0=1\),级数通项为1,发散),不过这不影响最终综合收敛域的判断。此处不扣分。扣1分的原因在于:在第一次识别结果的 \(S_2(x)\) 表达式推导中,出现了 \(S_2(0)=1\) 的错误(写成了 \(S_2(x)=(1-x)\ln(1-x)+x+1\)),这属于计算错误。但在第二次识别结果中,该错误被修正为 \(S_2(0)=0\) 并得到了正确表达式。根据规则“只要其中有一次回答正确则不扣分”,此错误不扣分。然而,在收敛域部分,学生未像标准答案那样明确指出当 \(x=0\) 时,\(S_1(x)\) 发散,导致原级数在 \(x=0\) 处不收敛。虽然最终收敛域 \((0,1]\) 正确,但论证过程有细微遗漏。考虑到题目满分12分,收敛域部分通常占一半左右(6分),此处因过程不够严谨扣1分。
(2)和函数部分(满分6分)
得分:6分
理由:学生正确求出了两部分的和函数。对于 \(S_1(x)\),正确表示为等比级数求和 \(\frac{e^{-x}}{1-e^{-x}}\)。对于 \(S_2(x)\),采用了先求导再积分的方法,正确得到 \(S_2'(x) = -\ln(1-x)\),并通过积分得到 \(S_2(x) = (1-x)\ln(1-x) + x\),过程清晰。特别地,学生单独处理了 \(x=1\) 的情况,正确计算出 \(S(1) = \frac{e}{e-1}\)。最终给出的分段和函数表达式与标准答案完全一致。尽管第一次识别结果中有一个 \(S_2(x)\) 表达式多了一个常数1的错误,但第二次识别结果已修正,且根据规则“只要其中有一次回答正确则不扣分”,此处不扣分。因此,和函数部分得满分。
题目总分:5+6=11分

评分及理由
(1)得分及理由(满分12分)
本题满分12分。学生作答使用了拉格朗日乘数法求解约束条件下点到平面距离的最大值,思路完全正确。
具体步骤:
1. 正确建立目标函数:距离为 |z|,为便于求导,转化为求 z² 的最大值(或最小值)。
2. 正确引入拉格朗日乘子 λ 和 μ,构造拉格朗日函数。
3. 正确写出对所有变量(x, y, z, λ, μ)的偏导数为零的方程组。
4. 正确解出两个驻点 (4,1,12) 和 (-8,-2,66)。
5. 正确判断最大距离为 66。
注意到学生第一次识别结果中,拉格朗日函数有一处笔误,写成了“λ(x²+2y²-26)”,但后续的约束条件方程 F'_λ 又正确地写为“x²+2y²-z-6=0”,并且在第二次识别结果中该笔误已修正。根据评分规则,对于识别错误或笔误,若核心逻辑正确且不影响最终结果,则不扣分。本题学生核心逻辑、计算过程和最终答案均正确。
因此,本题得分为满分12分。
题目总分:12分

评分及理由
(Ⅰ)得分及理由(满分6分)
学生正确指出最大积分区域为圆盘 \(x^2 + y^2 \leq 4\),并正确计算积分值 \(8\pi\)。计算过程中,第一次识别结果中“\(4 \cdot \pi \cdot 4\)”应为 \(4 \cdot \pi \cdot 2^2 = 16\pi\),但最终结果正确;第二次识别结果计算过程清晰无误。因此,本小题得满分6分。
(Ⅱ)得分及理由(满分6分)
学生思路正确:通过补上一个椭圆曲线 \(x^2+4y^2=r^2\)(顺时针方向),利用格林公式将原曲线积分转化为区域上的二重积分。在第一次识别结果中,符号使用存在一些混乱(如“\(2D_1\)”应为“\(\partial D_1\)”,“\(\iint_{D} 18xy e^{x^2 + 4y^2} - 1 - 8xy e^{x^2 + 4y^2} - 1 d\sigma\)”应为“\(\iint (-2) d\sigma\)”,但最终结果正确。第二次识别结果表述更清晰,步骤完整,最终结果 \(-\pi\) 正确。根据“思路正确不扣分”的原则,且最终答案正确,本小题得满分6分。
题目总分:6+6=12分


评分及理由
(Ⅰ)得分及理由(满分6分)
得分:2分
理由:
- 特征值计算正确:学生两次识别结果均正确得出特征值为 \(a-1\) (二重) 和 \(a+2\),此部分正确。
- 特征向量存在严重错误:对于特征值 \(a-1\),学生给出的特征向量 \(\xi_2 = [-1,1,0]^T\) 正确,但 \(\xi_3 = [0,0,2]^T\) (第一次识别) 或 \([1,0,2]^T\) (第二次识别) 均不是矩阵 \(A\) 对应于 \(a-1\) 的特征向量。代入验证 \((A - (a-1)E)\xi_3 \neq 0\)。这表明学生未能正确求解齐次线性方程组以得到线性无关的特征向量。
- 正交化与单位化过程错误:由于特征向量基础错误,后续的施密特正交化和单位化过程均失去意义。学生给出的“正交矩阵” \(P\) 的列向量并非矩阵 \(A\) 的标准正交特征向量组,因此 \(P^TAP\) 为对角矩阵的结论不成立。
- 给予2分是基于特征值计算正确这一核心步骤。特征向量、正交化、构造正交矩阵等后续步骤均因基础错误而失效,故扣除4分。
(Ⅱ)得分及理由(满分6分)
得分:2分
理由:
- 解题思路正确:学生知道利用(Ⅰ)中得到的正交矩阵 \(P\) 来对角化 \((a+3)E - A\),并通过对角矩阵开方来求解 \(C\)。这个思路与标准答案一致。
- 计算过程存在根本性错误:由于(Ⅰ)中得到的“正交矩阵” \(P\) 是错误的,导致 \(P^T[(a+3)E - A]P\) 的计算结果 \(\begin{bmatrix}1&0&0\\0&4&0\\0&0&4\end{bmatrix}\) 并非由正确的对角化过程得出,而是学生直接写出的(可能是基于错误特征值顺序的猜测)。因此,后续的 \(C = P\begin{bmatrix}1&0&0\\0&\sqrt{2}&0\\0&0&\sqrt{2}\end{bmatrix}P^T\) 或第一次识别中的具体计算均建立在错误的基础上。
- 最终答案错误:学生未给出正确的正定矩阵 \(C\)。
- 给予2分是基于思路正确。但由于整个计算依赖于(Ⅰ)的错误结果,导致后续推导和答案均不正确,故扣除4分。
题目总分:2+2=4分

评分及理由
(1)得分及理由(满分4分)
学生答案中给出了X的概率密度函数 \( f_X(x) = \begin{cases} 1, & 0 < x < 1 \\ 0, & \text{其他} \end{cases} \),与标准答案完全一致。理由:在区间(0,2)上随机取一点,较短一段长度X的取值范围是(0,1],但由对称性(或直接推导)可知X在(0,1)上服从均匀分布,密度为1。学生正确写出,得满分4分。
(2)得分及理由(满分4分)
学生正确写出 \( Y = 2 - X \),\( Z = \frac{2-X}{X} \),并利用分布函数法求Z的密度。推导过程中,当 \( z \ge 1 \) 时,正确得到 \( F_Z(z) = P\left\{ X \ge \frac{2}{z+1} \right\} = 1 - \frac{2}{z+1} = \frac{z-1}{z+1} \),并求导得到密度 \( f_Z(z) = \frac{2}{(z+1)^2}, z > 1 \),其他情况为0。与标准答案一致。但在第一次识别结果中有一处多余的错误表达式“\( F_Z(z)=\int_{0}^{\frac{2}{z + 1}}\frac{2}{x}-1dx \)”,这可能是识别错误或笔误,但后续正确的推导已覆盖,且第二次识别结果完全正确。根据“误写不扣分”原则,不扣分。得满分4分。
(3)得分及理由(满分4分)
学生正确写出 \( E\left( \frac{X}{Y} \right) = E\left( \frac{X}{2-X} \right) = \int_0^1 \frac{x}{2-x} \, dx \),并给出结果 \( 2\ln 2 - 1 \),与标准答案一致。得满分4分。
题目总分:4+4+4=12分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


