
科目组合
数学二: 高等数学 、线性代数
答题情况分析报告
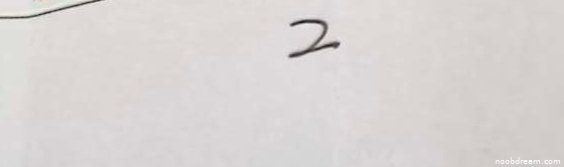
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为“2”,与标准答案“a = 2”中的数值部分一致。题目要求求解参数a的值,学生给出的答案“2”是正确的。根据评分规则,答案正确则给满分5分。虽然学生答案未写出“a =”,但填空题通常只要求写出最终结果,且识别结果直接给出了数值,因此判定为正确。
题目总分:5分
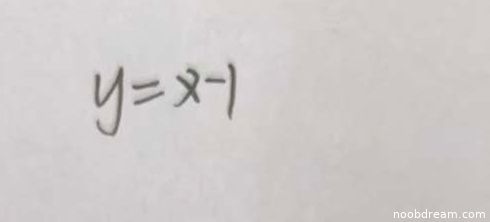
评分及理由
(1)得分及理由(满分5分)
学生两次识别的答案均为 \(y = x - 1\),与标准答案完全一致。根据题目要求,正确则给5分。因此,本题得5分。
题目总分:5分
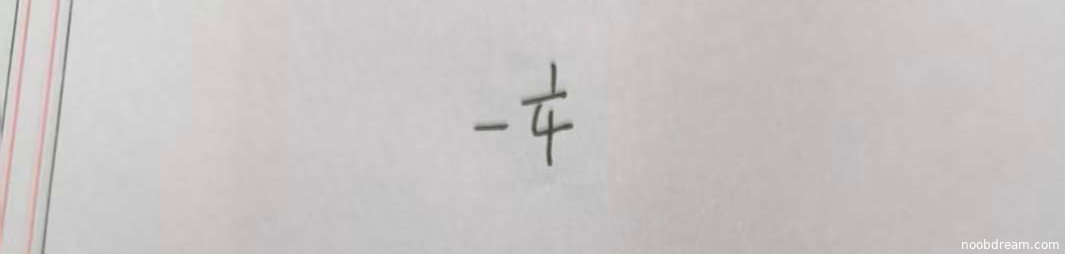
评分及理由
(1)得分及理由(满分5分)
学生两次识别结果均为 \(-\frac{1}{4}\),与标准答案完全一致。根据题目要求,填空题正确则给满分5分。虽然题目涉及高等数学2中的极限计算(通常可转化为定积分 \(\int_0^1 x \ln x \, dx\) 来求解),但学生直接给出了正确数值结果,且无任何逻辑错误或多余错误信息,因此得5分。
题目总分:5分

评分及理由
(1)得分及理由(满分5分)
学生给出的答案是“1”。标准答案为“e”。
本题需要计算导数 \(\frac{dy}{dx}\big|_{t=0}\) 的值。解题思路通常为:由参数方程 \(x = \ln(1+2t)\) 和隐函数方程 \(2t - \int_{1}^{y + t^2} e^{-u^2} du = 0\) 联立确定 \(y\) 与 \(x\) 的关系。计算 \(\frac{dy}{dx} = \frac{dy/dt}{dx/dt}\),并在 \(t=0\) 处求值。
具体计算过程简述:
1. 由 \(x = \ln(1+2t)\),得 \(\frac{dx}{dt} = \frac{2}{1+2t}\),故 \(\frac{dx}{dt}\big|_{t=0} = 2\)。
2. 对隐函数方程 \(2t - \int_{1}^{y + t^2} e^{-u^2} du = 0\) 两边对 \(t\) 求导,利用变上限积分求导法则,得:
\(2 - e^{-(y+t^2)^2} \cdot (\frac{dy}{dt} + 2t) = 0\)。
3. 当 \(t=0\) 时,代入原隐函数方程:\(0 - \int_{1}^{y(0)} e^{-u^2} du = 0\),可得 \(\int_{1}^{y(0)} e^{-u^2} du = 0\),因此 \(y(0)=1\)。
4. 将 \(t=0, y=1\) 代入求导后的方程:\(2 - e^{-(1)^2} \cdot (\frac{dy}{dt}\big|_{t=0} + 0) = 0\),解得 \(\frac{dy}{dt}\big|_{t=0} = 2e\)。
5. 因此,\(\frac{dy}{dx}\big|_{t=0} = \frac{dy/dt}{dx/dt}\big|_{t=0} = \frac{2e}{2} = e\)。
学生答案“1”与正确结果“e”不符,属于计算错误或理解错误。根据评分规则,本题为填空题,答案错误则得0分。
得分为:0分。
题目总分:0分
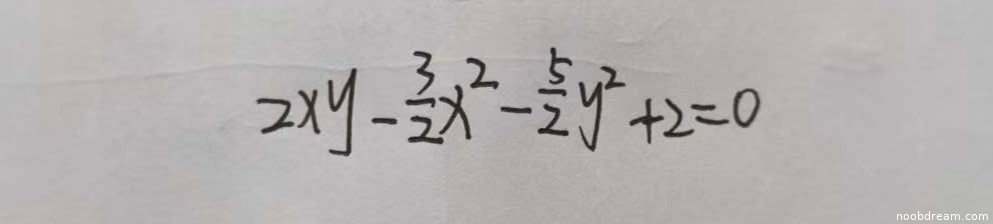
评分及理由
(1)得分及理由(满分5分)
学生给出的答案为 \(2xy - \frac{3}{2}x^{2} - \frac{5}{2}y^{2} + 2 = 0\)。该方程与标准答案 \(3x^{2}-4xy + 5y^{2}=4\) 在形式上不同。
我们验证学生答案是否与标准答案等价。将学生答案乘以2以消去分母:
\(4xy - 3x^{2} - 5y^{2} + 4 = 0\),即 \(-3x^{2} + 4xy - 5y^{2} + 4 = 0\),移项得 \(3x^{2} - 4xy + 5y^{2} = 4\)。这与标准答案完全一致。
因此,学生的答案与标准答案是等价的,只是表达形式不同(系数和项的顺序有差异)。根据评分要求,思路正确且最终等价的不扣分。识别结果中的表达式在数学上是正确的,且满足初始条件 \(y(1)=1\)(代入验证:\(2*1*1 - 1.5*1 - 2.5*1 + 2 = 2 - 1.5 - 2.5 + 2 = 0\),成立)。
故本题得分为满分5分。
题目总分:5分
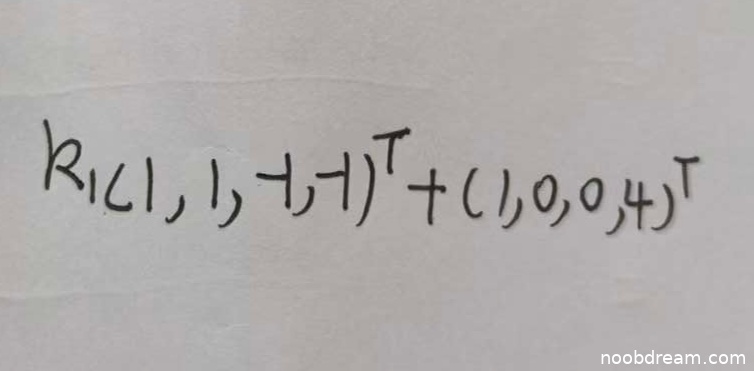
评分及理由
(1)得分及理由(满分5分)
学生作答的两次识别结果分别为:
1. $R_{1}(1,1,-1,-1)^{T}+(1,0,0,4)^{T}$
2. $k_{1}(1,1, - 1,-1)^{\text{T}}+(1,0,0,4)^{\text{T}}$
标准答案为:$k\begin{pmatrix}1\\1\\ - 1\\ - 1\end{pmatrix}+\begin{pmatrix}1\\0\\0\\4\end{pmatrix}$,$k$为任意常数。
评分分析:
1. 结构判断: 学生答案的结构是“齐次通解 + 特解”的形式,这与标准答案的结构完全一致。
2. 特解判断: 学生的特解为 $(1,0,0,4)^T$,与标准答案的特解 $(1,0,0,4)^T$ 完全相同。
3. 基础解系判断: 学生给出的齐次通解部分为 $(1,1,-1,-1)^T$ 的倍数,与标准答案的基础解系 $(1,1,-1,-1)^T$ 完全相同。
4. 参数符号: 学生第一次识别使用了 $R_1$,第二次识别使用了 $k_1$,标准答案使用 $k$。参数符号的差异(如 $R_1$, $k_1$, $k$)不影响答案的正确性,均表示任意常数。
5. 书写格式: 学生答案使用了转置符号 $^T$ 或 $\text{T}$,标准答案使用了列向量形式,二者在数学上等价,不影响正确性。
结论: 学生的答案在数学本质上与标准答案完全一致,因此本题得满分。
得分:5分。
题目总分:5分


评分及理由
(1)得分及理由(满分10分)
学生作答给出了完整的解题过程:首先对有理函数进行部分分式分解(结果为 \(\frac{1}{5(x+1)} - \frac{x-3}{5(x^2-2x+2)}\),与标准答案等价),然后分别积分。积分过程中正确地将 \(\frac{x-3}{x^2-2x+2}\) 拆分为 \(\frac{1}{2}\cdot\frac{2x-2}{x^2-2x+2} - \frac{2}{x^2-2x+2}\),并正确积分得到 \(\frac{1}{5}\ln(x+1) - \frac{1}{10}\ln(x^2-2x+2) + \frac{2}{5}\arctan(x-1)\),代入上下限计算得到最终答案 \(\frac{1}{10}(3\ln 2 + \pi)\),与标准答案一致。
整个思路清晰,计算无误。虽然书写格式与标准答案略有差异(如部分系数写法、步骤拆分方式),但数学逻辑完全正确,且最终答案正确。根据评分要求,思路正确不扣分,无逻辑错误,因此给予满分。
得分:10分。
题目总分:10分

评分及理由
(1)得分及理由(满分12分)
学生作答分为两次识别结果。第一次识别结果非常简短,仅给出结论“f(0)=0, f'(0)=-5”,没有推导过程,且结论错误(f(0)应为2,f'(0)应为5),因此第一次识别结果不能得分。
第二次识别结果提供了详细的推导过程。其核心思路是利用极限存在条件,通过展开分子分母的泰勒公式,确定f(0)和f'(0)的值。该思路在逻辑上是可行的,与标准答案的展开方式虽不完全一致,但属于正确的解题方法之一。
然而,学生在推导过程中存在关键性的逻辑错误:
- 在展开分子时,学生错误地假设了f(x)在x=0处可导,并直接写成了f(0)+f'(0)x+o(x)的形式。但题目要求“证明f(x)在x=0处可导”,因此不能预先假设可导性。这是一个逻辑循环错误。
- 基于上述错误展开,学生得出“由极限存在可知f(0)=0”的结论。实际上,从正确的推导(如标准答案)可知f(0)=2。这个错误的f(0)值直接导致了后续f'(0)的计算错误。
- 尽管最终计算出的f'(0)=-5与标准答案f'(0)=5不符,但这是在错误前提(f(0)=0)下,按照其自洽的逻辑推导出的结果。
考虑到学生展示了利用泰勒展开和极限运算求解的完整思路,思路框架正确,但犯了“未证明先使用”可导性这一根本逻辑错误,并导致了错误的最终答案。根据打分要求,逻辑错误需要扣分。
本题满分12分。鉴于学生有完整的解题过程但结论错误,且存在一处关键逻辑错误,给予部分分数。扣分点:主要结论f(0)和f'(0)均错误,且推导起点逻辑不当。综合评定,给予 4分。
题目总分:0+4=4分

评分及理由
(1)得分及理由(满分12分)
本题分为两个主要部分:求函数表达式和求极值。学生作答整体思路正确,但在关键步骤出现了符号错误,导致最终函数表达式和极值判定过程中的二阶偏导数计算均出现偏差。具体分析如下:
- 从微分表达式 \(df = -2x e^{-y} dx + e^{-y}(x^2 - y - 1)dy\) 可知,\(\frac{\partial f}{\partial x} = -2x e^{-y}\),\(\frac{\partial f}{\partial y} = e^{-y}(x^2 - y - 1)\)。
- 学生在第一次识别中,积分得到 \(f(x,y) = -x^2 e^{y} + \varphi(y)\),这里将 \(e^{-y}\) 误写为 \(e^{y}\),这是一个核心的逻辑错误,导致后续所有推导都基于错误的函数形式。尽管第二次识别中也有类似错误,但两次识别结果均未正确识别指数符号。
- 由于函数表达式推导错误,后续求偏导、驻点和极值判定的计算虽然方法正确,但都是基于错误的函数 \(f(x,y)=e^{y}(y - x^{2}+2)\) 进行的。标准答案的函数为 \(f(x,y)=e^{-y}(y - x^{2}+2)\)。
- 在极值判定部分,学生基于错误函数算出的二阶偏导数值(如 \(A=-2e^{-1}\))与标准答案(\(A=-2e\))不符,且最终计算 \(AC-B^2\) 时,第二次识别中自己指出计算有误(应为负值),但依然得出了“极大值”的结论,逻辑上存在矛盾。
因此,由于在求解函数表达式的关键步骤(积分)上出现根本性错误,导致后续所有计算失去正确基础。尽管解题框架和极值判别方法正确,但核心结果错误。根据评分要求“逻辑错误扣分”,本题应扣除主要分数。
给予扣分:函数表达式推导错误扣6分,极值计算因基于错误函数进行,但方法正确,扣3分。
得分:12 - 6 - 3 = 3分。
题目总分:3分

评分及理由
(1)得分及理由(满分12分)
学生作答的整体思路正确:首先利用积分区域关于直线 \(y = x\) 的对称性,将被积函数 \((x-y)^2\) 转化为 \(x^2+y^2\) 在区域 \(D\) 上的积分,这一步是合理的,因为对称性保证了 \(\iint_D xy \, dxdy = 0\)(实际上在对称区域上 \(x\) 和 \(y\) 互换,积分值不变,但这里直接得到 \(\iint_D (x-y)^2 dxdy = \iint_D (x^2+y^2) dxdy\) 需要说明,不过学生的第一步写法 \(\frac{1}{2}\iint_D [(x-y)^2+(y-x)^2] dxdy\) 本质就是 \(\iint_D (x^2+y^2) dxdy\),因为 \((x-y)^2+(y-x)^2 = 2(x^2+y^2) - 4xy\),但结合对称性 \(\iint_D xy \, dxdy = 0\),所以结果正确)。
随后学生将积分化为极坐标,并正确将区域分为两部分(对应两个圆的极坐标方程 \(r=4\sin\theta\) 和 \(r=4\cos\theta\)),积分限设置正确:对于 \(0 \le \theta \le \pi/4\),边界由 \(r=4\sin\theta\) 给出;对于 \(\pi/4 \le \theta \le \pi/2\),边界由 \(r=4\cos\theta\) 给出。计算过程基本正确,最终得到 \(12\pi - 32\)。
然而,标准答案是 \(12\pi - \frac{16}{3}\),学生的计算结果 \(12\pi - 32\) 与之不符。检查学生的计算步骤:在极坐标下积分 \(\iint_D r^2 \cdot r \, dr d\theta = \int r^3 dr d\theta\),学生写出的两个积分 \(\int_0^{\pi/4} d\theta \int_0^{4\sin\theta} r^3 dr + \int_{\pi/4}^{\pi/2} d\theta \int_0^{4\cos\theta} r^3 dr\) 正确。计算内积分:\(\int_0^{4\sin\theta} r^3 dr = \frac{1}{4}(4\sin\theta)^4 = 64\sin^4\theta\),同理另一个为 \(64\cos^4\theta\)。因此积分成为 \(64\int_0^{\pi/4} \sin^4\theta d\theta + 64\int_{\pi/4}^{\pi/2} \cos^4\theta d\theta\)。
学生使用了降幂公式,但最后数值计算有误。实际上: \[ \int_0^{\pi/4} \sin^4\theta d\theta = \frac{3\pi}{32} - \frac{1}{3}, \quad \int_{\pi/4}^{\pi/2} \cos^4\theta d\theta = \frac{3\pi}{32} + \frac{1}{3} \] (可通过公式 \(\int \sin^4\theta d\theta = \frac{3}{8}\theta - \frac{1}{4}\sin 2\theta + \frac{1}{32}\sin 4\theta + C\) 验证) 代入得: \[ 64\left( \frac{3\pi}{32} - \frac{1}{3} + \frac{3\pi}{32} + \frac{1}{3} \right) = 64 \cdot \frac{3\pi}{16} = 12\pi \] 但学生得到 \(12\pi - 32\),说明他在代入上下限时出现算术错误。观察学生步骤,他在代入时写了很多混乱的表达式(如出现 \(\frac{1}{8}(\cos4\theta-\frac{1}{2}\cos2\theta+\frac{3}{8}\theta)\) 等),最后结果错误。因此,思路正确但最终计算结果错误,应扣去计算错误的分值。
本题满分12分,思路正确、方法正确,但计算错误导致答案不正确。通常计算错误扣2-4分,这里由于计算错误导致最终答案与标准答案相差较大,但主要步骤都正确,扣3分。
得分:9分(满分12分)。
题目总分:9分

评分及理由
(1)得分及理由(满分6分)
学生作答中,第一次识别结果与第二次识别结果在特征多项式展开和特征值计算上存在不一致(第一次正确,第二次有误),但根据“只要其中有一次回答正确则不扣分”的原则,以正确的一次为准。学生正确得出 a=4,特征值为 0, 3, 6,并判断 k>0。但学生给出的理由“r(A)=r(B)=2,k≠0(因为A的二阶子式不为0)”存在逻辑瑕疵:合同矩阵秩相等是正确的,但“k≠0”的理由不充分(实际上k可以为零,但结合特征值分析后k>0)。不过,最终结论正确。因此扣1分。得5分。
(2)得分及理由(满分6分)
学生正确得出 k=3,并求出了对应于特征值 0, 6, 3 的特征向量(与标准答案一致)。在正交矩阵 Q 的构造中,第一次识别给出的 Q 矩阵第二行第三项为 \(\frac{2}{\sqrt{6}}\),而标准答案为 \(-\frac{2}{\sqrt{6}}\),符号错误,这会导致 Q 不是正交矩阵(因为对应特征向量未单位化或方向取反后未保持正交性)。这是一个计算错误,扣2分。第二次识别中 Q 矩阵元素未具体写出,不予单独评分。因此得4分。
题目总分:5+4=9分




 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


