
科目组合
数学二: 高等数学 、线性代数
答题情况分析报告
-1
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是“-1”。
题目要求当 \(x \to 0\) 时,函数 \(f(x)=a x+b x^{2}+\ln (1+x)\) 与 \(g(x)=e^{x^{2}}-\cos x\) 是等价无穷小。这意味着 \(\lim_{x \to 0} \frac{f(x)}{g(x)} = 1\)。
首先,将 \(f(x)\) 和 \(g(x)\) 在 \(x=0\) 处进行泰勒展开:
- \(\ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} + o(x^3)\)
- \(e^{x^2} = 1 + x^2 + o(x^2)\)
- \(\cos x = 1 - \frac{x^2}{2} + o(x^2)\)
因此: \[ f(x) = a x + b x^2 + \left( x - \frac{x^2}{2} + o(x^2) \right) = (a+1)x + \left(b - \frac{1}{2}\right)x^2 + o(x^2) \] \[ g(x) = (1 + x^2 + o(x^2)) - \left(1 - \frac{x^2}{2} + o(x^2)\right) = \frac{3}{2}x^2 + o(x^2) \]
要使 \(f(x)\) 与 \(g(x)\) 为等价无穷小,它们必须是同阶无穷小,且极限为1。观察 \(g(x)\) 的展开式,其最低阶项为 \(x^2\) 项。因此,\(f(x)\) 的 \(x\) 项系数必须为零,以避免 \(f(x)\) 成为比 \(g(x)\) 更高阶的无穷小(或无穷大)。
令 \(x\) 项系数为零:\(a+1 = 0\),解得 \(a = -1\)。
此时,\(f(x) = \left(b - \frac{1}{2}\right)x^2 + o(x^2)\)。
计算极限: \[ \lim_{x \to 0} \frac{f(x)}{g(x)} = \lim_{x \to 0} \frac{\left(b - \frac{1}{2}\right)x^2 + o(x^2)}{\frac{3}{2}x^2 + o(x^2)} = \frac{b - \frac{1}{2}}{\frac{3}{2}} \]
令该极限等于1: \[ \frac{b - \frac{1}{2}}{\frac{3}{2}} = 1 \quad \Rightarrow \quad b - \frac{1}{2} = \frac{3}{2} \quad \Rightarrow \quad b = 2 \]
因此,\(a = -1\),\(b = 2\),所求 \(ab = (-1) \times 2 = -2\)。
学生给出的答案是“-1”,这可能是他/她只计算出了 \(a\) 的值,而题目要求的是 \(a\) 与 \(b\) 的乘积 \(ab\)。学生的答案与标准答案“-2”不符。
根据题目要求,本题为填空题,正确则给5分,错误则给0分,禁止给步骤分。因此,该答案错误,得0分。
题目总分:0分
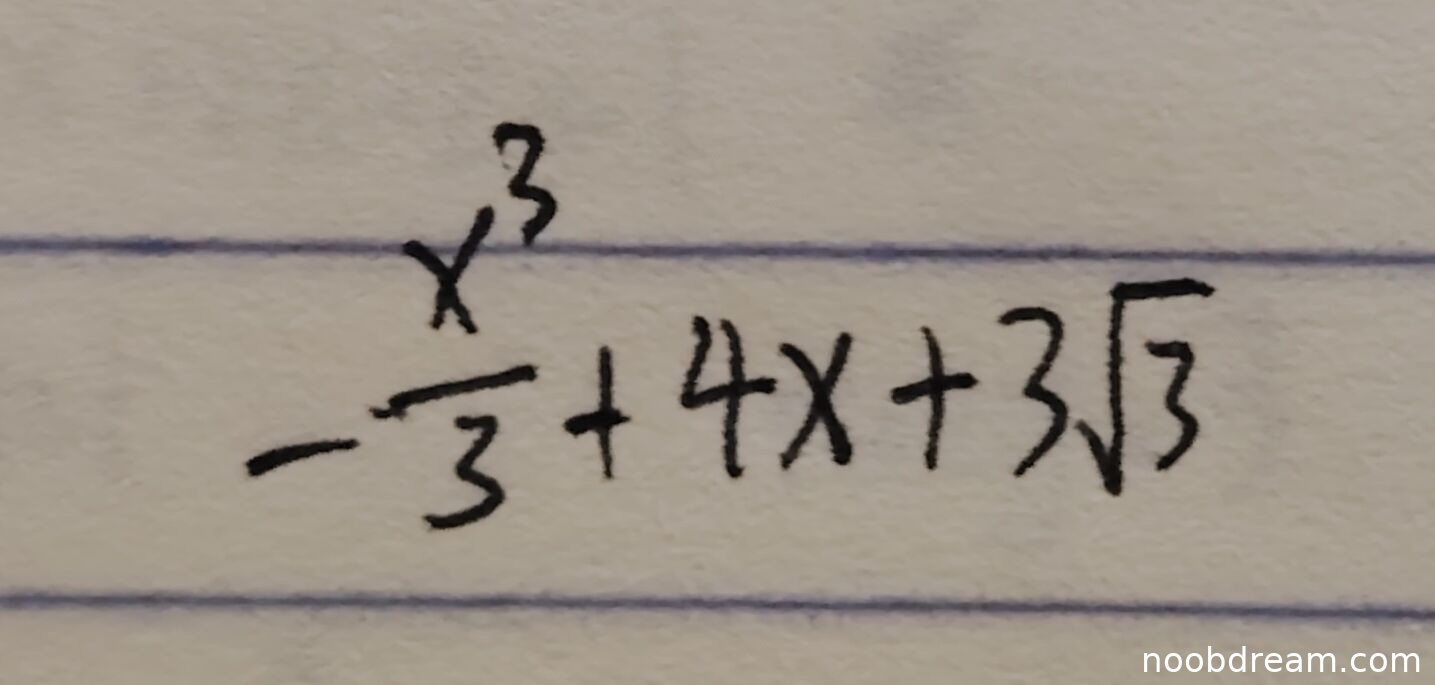
评分及理由
(1)得分及理由(满分5分)
学生给出的两个识别结果均为 \(-\frac{x^{3}}{3}+4x + 3\sqrt{3}\),这与标准答案 \(\sqrt{3}+\frac{4}{3} \pi\) 完全不同。
题目要求计算曲线 \(y=\int_{-\sqrt{3}}^{x} \sqrt{3-t^{2}} ~d t\) 的弧长。这是一个定积分定义的函数,其弧长公式为 \(L = \int_{a}^{b} \sqrt{1 + [y'(x)]^2} dx\)。首先需要求导 \(y'(x) = \sqrt{3 - x^2}\),然后代入弧长公式。被积函数 \(\sqrt{1 + (3 - x^2)} = \sqrt{4 - x^2}\)。接下来需要确定积分区间。原函数 \(y(x)\) 的定义域由被积函数 \(\sqrt{3-t^2}\) 决定,即 \(t \in [-\sqrt{3}, \sqrt{3}]\),所以 \(x\) 的取值区间也是 \([-\sqrt{3}, \sqrt{3}]\)。因此弧长 \(L = \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{4 - x^2} dx\)。这个积分可以通过几何意义(半圆面积)或三角代换来计算,结果为 \(\sqrt{3} + \frac{4\pi}{3}\)。
学生给出的答案是一个关于 \(x\) 的多项式加上常数,这完全不符合弧长应为一个常数的基本事实。这表明学生可能错误地理解了题目,例如可能计算了原函数 \(y(x)\) 本身,或者进行了错误的运算。这是一个根本性的逻辑错误,答案与标准答案不符。
根据评分要求,本题为填空题,正确则给5分,错误则给0分,禁止给步骤分。因此,本题得分为0分。
题目总分:0分
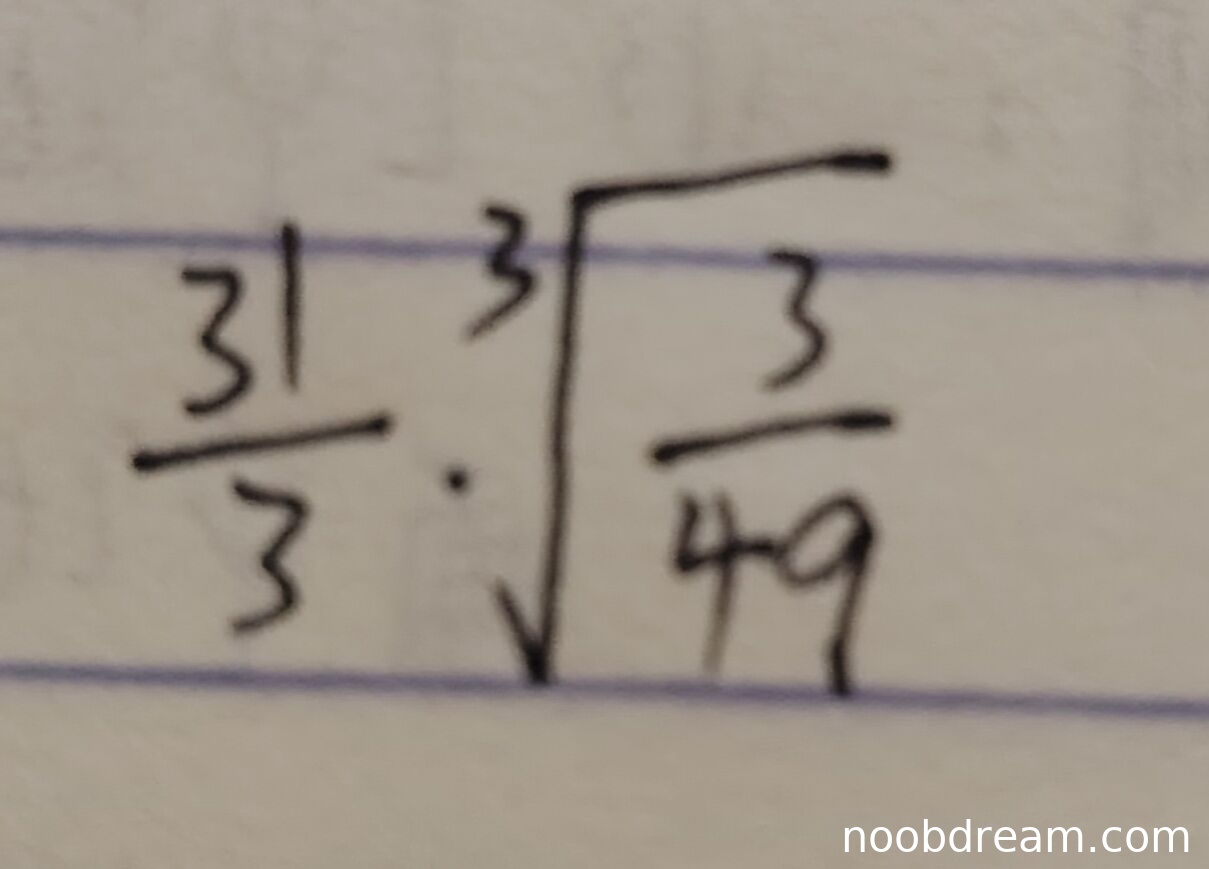
评分及理由
(1)得分及理由(满分5分)
学生答案 \(\frac{31}{3}\cdot\sqrt[3]{\frac{3}{49}}\) 与标准答案 \(-\frac{11}{9}\) 在数值和形式上均不同,且不是由字符识别错误导致的等价答案,因此答案错误。根据填空题评分规则(正确5分,错误0分,无步骤分),本题得 0 分。
题目总分:0分
1
评分及理由
(1)得分及理由(满分5分)
学生给出的答案为“1”。
本题需要根据已知条件 \(f(x+2)-f(x)=x\) 和 \(\int_{0}^{2} f(x) d x=0\),求解 \(\int_{1}^{3} f(x) d x\)。
一种标准解法如下:
由 \(f(x+2)-f(x)=x\),可得 \(f(x+2) = f(x) + x\)。
所求积分 \(\int_{1}^{3} f(x) dx = \int_{1}^{2} f(x) dx + \int_{2}^{3} f(x) dx\)。
对于第二部分,令 \(t = x-2\),则当 \(x \in [2, 3]\) 时,\(t \in [0, 1]\),且 \(f(x) = f(t+2) = f(t) + t\)。
因此,\(\int_{2}^{3} f(x) dx = \int_{0}^{1} [f(t) + t] dt = \int_{0}^{1} f(t) dt + \int_{0}^{1} t dt = \int_{0}^{1} f(x) dx + \frac{1}{2}\)。
于是,\(\int_{1}^{3} f(x) dx = \int_{1}^{2} f(x) dx + \int_{0}^{1} f(x) dx + \frac{1}{2}\)。
注意到 \(\int_{0}^{2} f(x) dx = \int_{0}^{1} f(x) dx + \int_{1}^{2} f(x) dx = 0\)。
所以,\(\int_{1}^{3} f(x) dx = 0 + \frac{1}{2} = \frac{1}{2}\)。
标准答案为 \(\frac{1}{2}\),学生答案为“1”,与标准答案不符。学生作答中未提供任何解题过程,仅给出了一个数字结果。根据题目要求“正确则给5分,错误则给0分”,且“禁止给步骤分”,因此该答案错误,得0分。
题目总分:0分
-3
评分及理由
(1)得分及理由(满分5分)
学生给出的答案是“-3”。
首先,我们需要分析题目。已知行列式: \[ D_1 = \begin{vmatrix} a & 0 & 1 \\ 1 & a & 1 \\ 1 & 2 & a \end{vmatrix} = 4 \] 要求计算行列式: \[ D_2 = \begin{vmatrix} 1 & a & 1 \\ 1 & 2 & a \\ a & b & 0 \end{vmatrix} \] 观察两个行列式,发现 \(D_2\) 的行是 \(D_1\) 的行经过轮换得到的:将 \(D_1\) 的第一行移到第三行,第二行移到第一行,第三行移到第二行,即进行一次“向上”的轮换(或等价地,两次行交换)。具体来说: \[ D_1: R_1=(a,0,1), R_2=(1,a,1), R_3=(1,2,a) \] \[ D_2: R_1'=(1,a,1), R_2'=(1,2,a), R_3'=(a,b,0) \] 比较 \(D_1\) 和 \(D_2\) 的前两行,\(D_2\) 的前两行正好是 \(D_1\) 的第二行和第三行。但 \(D_2\) 的第三行是 \((a, b, 0)\),而 \(D_1\) 的第一行是 \((a, 0, 1)\),两者不同。因此不能直接通过行置换得到关系。
我们需要利用已知条件求出 \(a\) 和 \(b\)。先计算 \(D_1\): \[ \begin{aligned} D_1 &= a \cdot \begin{vmatrix} a & 1 \\ 2 & a \end{vmatrix} - 0 \cdot \begin{vmatrix} 1 & 1 \\ 1 & a \end{vmatrix} + 1 \cdot \begin{vmatrix} 1 & a \\ 1 & 2 \end{vmatrix} \\ &= a(a \cdot a - 1 \cdot 2) + 1(1 \cdot 2 - a \cdot 1) \\ &= a(a^2 - 2) + (2 - a) \\ &= a^3 - 2a + 2 - a \\ &= a^3 - 3a + 2 \end{aligned} \] 已知 \(D_1 = 4\),所以: \[ a^3 - 3a + 2 = 4 \quad \Rightarrow \quad a^3 - 3a - 2 = 0 \] 通过试根,\(a = 2\) 是根:\(8 - 6 - 2 = 0\)。因式分解: \[ a^3 - 3a - 2 = (a - 2)(a^2 + 2a + 1) = (a - 2)(a + 1)^2 \] 所以 \(a = 2\) 或 \(a = -1\)。
现在计算 \(D_2\): \[ D_2 = \begin{vmatrix} 1 & a & 1 \\ 1 & 2 & a \\ a & b & 0 \end{vmatrix} \] 按第三列展开(或直接计算): \[ \begin{aligned} D_2 &= 1 \cdot \begin{vmatrix} 1 & 2 \\ a & b \end{vmatrix} - a \cdot \begin{vmatrix} 1 & a \\ a & b \end{vmatrix} + 0 \cdot \begin{vmatrix} 1 & a \\ 1 & 2 \end{vmatrix} \\ &= (1 \cdot b - 2 \cdot a) - a(1 \cdot b - a \cdot a) \\ &= (b - 2a) - a(b - a^2) \\ &= b - 2a - ab + a^3 \end{aligned} \] 即 \(D_2 = a^3 - 2a + b(1 - a)\)。
为了确定 \(b\),我们需要利用题目隐含的条件吗?题目没有直接给出 \(b\),但两个行列式可能有联系。观察 \(D_1\) 和 \(D_2\),如果我们将 \(D_1\) 的第三行乘以某个数加到第二行等,可能得到 \(D_2\) 的某行?另一种思路:题目可能期望我们利用行列式性质,发现 \(D_2\) 与 \(D_1\) 有某种线性关系,从而不需要知道 \(b\) 就能算出 \(D_2\)。
考虑 \(D_2\) 的第三行 \((a, b, 0)\) 与 \(D_1\) 的第一行 \((a, 0, 1)\) 的关系。如果令 \(b\) 满足某种条件,使得 \(D_2\) 可以通过 \(D_1\) 经过行初等变换得到?但这样会改变行列式的值。
更直接的方法:将 \(D_2\) 与 \(D_1\) 联系起来。将 \(D_1\) 的行列式进行行交换:交换第一行和第三行,得到: \[ \begin{vmatrix} 1 & 2 & a \\ 1 & a & 1 \\ a & 0 & 1 \end{vmatrix} = -D_1 = -4 \] (因为交换一次行,行列式变号)。
再交换第二行和第三行: \[ \begin{vmatrix} 1 & 2 & a \\ a & 0 & 1 \\ 1 & a & 1 \end{vmatrix} = -(-4) = 4 \] (因为再交换一次,又变号,所以回到原来的值?不对,仔细算:第一次交换后是 -4,第二次交换后是 -(-4)=4?实际上:设原行列式为 \(D\),交换1、3行得 \(-D\),再交换2、3行(在新的矩阵中交换第二行和第三行)得 \(-(-D) = D\)。所以两次交换后等于原行列式 \(D_1 = 4\)。但得到的行列式是: \[ \begin{vmatrix} 1 & 2 & a \\ a & 0 & 1 \\ 1 & a & 1 \end{vmatrix} \] 这与 \(D_2 = \begin{vmatrix} 1 & a & 1 \\ 1 & 2 & a \\ a & b & 0 \end{vmatrix}\) 仍然不同。
尝试另一种行交换顺序:将 \(D_1\) 的第一行移到第三行(即依次交换第一行和第二行,然后交换新的第二行和第三行): 步骤:原 \(D_1\) 矩阵: \[ R_1: (a,0,1), R_2: (1,a,1), R_3: (1,2,a) \] 交换 \(R_1\) 和 \(R_2\): \[ R_1': (1,a,1), R_2': (a,0,1), R_3': (1,2,a) \] 再交换 \(R_2'\) 和 \(R_3'\): \[ R_1'': (1,a,1), R_2'': (1,2,a), R_3'': (a,0,1) \] 得到矩阵: \[ \begin{vmatrix} 1 & a & 1 \\ 1 & 2 & a \\ a & 0 & 1 \end{vmatrix} \] 这个行列式与 \(D_2\) 相比,只有第三行第三列元素不同:这里是 1,\(D_2\) 是 0;且第三行第二列这里是 0,\(D_2\) 是 \(b\)。
记上述行列式为 \(D_3 = \begin{vmatrix} 1 & a & 1 \\ 1 & 2 & a \\ a & 0 & 1 \end{vmatrix}\)。由于经过两次行交换(每次变号),所以 \(D_3 = (-1)^2 D_1 = D_1 = 4\)。
现在,将 \(D_3\) 的第三列乘以 -1 加到第一列?或者利用行列式性质:将 \(D_3\) 的第三行减去第一行的 \(a\) 倍?我们想得到 \(D_2\)。注意 \(D_2\) 的第三行是 \((a, b, 0)\),而 \(D_3\) 的第三行是 \((a, 0, 1)\)。如果我们将 \(D_3\) 的第三列乘以 -1 加到第三行?不对,那是列操作。
更简单:计算 \(D_3\) 和 \(D_2\) 的差值。由于行列式是线性的,我们可以将 \(D_2\) 表示为 \(D_3\) 加上某个修正。但直接计算 \(D_3\): \[ D_3 = \begin{vmatrix} 1 & a & 1 \\ 1 & 2 & a \\ a & 0 & 1 \end{vmatrix} \] 按第三行展开: \[ D_3 = a \begin{vmatrix} a & 1 \\ 2 & a \end{vmatrix} - 0 \cdot \begin{vmatrix} 1 & 1 \\ 1 & a \end{vmatrix} + 1 \cdot \begin{vmatrix} 1 & a \\ 1 & 2 \end{vmatrix} = a(a^2 - 2) + (2 - a) = a^3 - 2a + 2 - a = a^3 - 3a + 2 \] 这正是 \(D_1\),所以 \(D_3 = 4\)。
现在,\(D_2\) 与 \(D_3\) 只有第三行不同。将 \(D_3\) 的第三行替换为 \((a, b, 0)\) 得到 \(D_2\)。利用行列式对行的线性性质:将 \(D_3\) 的第三行拆成两部分:\((a, b, 0) = (a, 0, 1) + (0, b, -1)\)。所以: \[ D_2 = \begin{vmatrix} 1 & a & 1 \\ 1 & 2 & a \\ a & 0 & 1 \end{vmatrix} + \begin{vmatrix} 1 & a & 1 \\ 1 & 2 & a \\ 0 & b & -1 \end{vmatrix} \] 即 \(D_2 = D_3 + \Delta\),其中 \(\Delta = \begin{vmatrix} 1 & a & 1 \\ 1 & 2 & a \\ 0 & b & -1 \end{vmatrix}\)。
计算 \(\Delta\):按第三行展开: \[ \Delta = 0 \cdot \begin{vmatrix} a & 1 \\ 2 & a \end{vmatrix} - b \begin{vmatrix} 1 & 1 \\ 1 & a \end{vmatrix} + (-1) \begin{vmatrix} 1 & a \\ 1 & 2 \end{vmatrix} = -b(a - 1) - (2 - a) = -b(a-1) - (2-a) \] 所以: \[ D_2 = 4 + [-b(a-1) - (2-a)] = 4 - b(a-1) - 2 + a = 2 + a - b(a-1) \] 这和我们之前直接算的 \(D_2 = a^3 - 2a + b(1-a)\) 一致(因为 \(a^3 - 2a = a(a^2-2)\),代入验证:\(a^3 - 2a + b(1-a) = a^3 - 2a + b - ab\),而 \(2 + a - b(a-1) = 2 + a - ab + b\),两者相等当且仅当 \(a^3 - 2a = 2 + a\),即 \(a^3 - 3a - 2 = 0\),这正是已知条件,所以一致)。
因此,要确定 \(D_2\),必须知道 \(b\)。但题目没有给出 \(b\),所以很可能 \(b\) 被消去了,即 \(D_2\) 的值与 \(b\) 无关。检查表达式 \(D_2 = a^3 - 2a + b(1-a)\)。已知 \(a^3 - 3a - 2 = 0\),所以 \(a^3 - 2a = 3a + 2\)?由 \(a^3 - 3a - 2 = 0\) 得 \(a^3 - 2a = a + 2\)。代入: \[ D_2 = (a + 2) + b(1 - a) \] 仍然含有 \(b\)。除非 \(1-a=0\) 即 \(a=1\),但 \(a=1\) 不满足方程(\(1-3-2=-4\neq0\))。所以 \(D_2\) 依赖于 \(b\)。
这意味着题目可能隐含了 \(b\) 的值。观察 \(D_1\) 和 \(D_2\) 的矩阵,可能 \(b\) 是某个特定值使得两个行列式有简单关系。或者题目本意是求 \(D_2\) 的值,而 \(b\) 是未知数,但答案却是常数,说明 \(b\) 被消去。我们检查是否漏了条件。将 \(D_1\) 和 \(D_2\) 看作关于 \(a, b\) 的方程,但只有一个方程 \(D_1=4\),无法确定两个变量,所以理论上 \(D_2\) 不唯一。但标准答案是 8,说明对于满足 \(a^3-3a-2=0\) 的 \(a\),存在某个 \(b\) 使得 \(D_2=8\),且这个 \(b\) 是确定的?不一定,因为对于不同的 \(a\),\(b\) 可以调整使 \(D_2=8\)。但题目是填空题,应该唯一。
再仔细看矩阵:\(D_1\) 的第三行是 \((1,2,a)\),\(D_2\) 的第二行是 \((1,2,a)\),完全相同。\(D_1\) 的第二行是 \((1,a,1)\),\(D_2\) 的第一行是 \((1,a,1)\),也相同。\(D_1\) 的第一行是 \((a,0,1)\),\(D_2\) 的第三行是 \((a,b,0)\)。所以 \(D_2\) 的第三行是由 \(D_1\) 的第一行交换第二和第三列,然后修改第二个元素?交换列会改变行列式的值(可能变号)。
考虑列操作:将 \(D_1\) 的第二列和第三列交换,得到: \[ \begin{vmatrix} a & 1 & 0 \\ 1 & 1 & a \\ 1 & a & 2 \end{vmatrix} \] 这不像 \(D_2\)。将 \(D_1\) 的第一行变成第三行,然后交换第二列和第三列?似乎复杂。
另一种思路:可能题目有笔误,原题中 \(D_2\) 的第三行应该是 \((a,0,1)\) 而不是 \((a,b,0)\)?但那样就是 \(D_3\),值为 4,不是答案 8。或者第三行是 \((a,2,0)\)?
我们假设标准答案 8 是正确的,那么由 \(D_2 = a^3 - 2a + b(1-a) = 8\),结合 \(a^3 - 3a - 2 = 0\),得 \(a^3 - 2a = a + 2\),所以 \(a + 2 + b(1-a) = 8\),即 \(b(1-a) = 6 - a\)。对于 \(a=2\),\(b(1-2)=6-2=4\),得 \(b(-1)=4\),\(b=-4\)。对于 \(a=-1\),\(b(1-(-1))=6-(-1)=7\),\(b \cdot 2 = 7\),\(b=3.5\)。所以 \(b\) 不唯一,但题目没有给出 \(b\),所以可能题目隐含了 \(a\) 的值是哪一个?通常取整数解 \(a=2\),那么 \(b=-4\),此时 \(D_2=8\)。但题目没有说 \(a\) 是整数,所以这只是一个猜测。
或许题目中 \(D_2\) 的第三行第二列不是 \(b\) 而是 0?即 \(\begin{vmatrix}1 & a & 1 \\ 1 & 2 & a \\ a & 0 & 0\end{vmatrix}\)?但那样答案也不是 8。
我们计算当 \(a=2\) 时,\(D_2 = 8 + b(1-2) = 8 - b\),要等于 8 则需 \(b=0\)。但若 \(a=2, b=0\),\(D_2 = 8\)。检查 \(D_1\):当 \(a=2\),\(D_1 = 8 - 6 + 2 = 4\),符合。所以当 \(a=2, b=0\) 时,\(D_2=8\)。但题目中 \(D_2\) 的第三行是 \((a, b, 0)\),若 \(b=0\),则第三行是 \((2,0,0)\),那么 \(D_2 = \begin{vmatrix}1 & 2 & 1 \\ 1 & 2 & 2 \\ 2 & 0 & 0\end{vmatrix}\),计算:按第三行展开,\(2 \cdot \begin{vmatrix}2 & 1 \\ 2 & 2\end{vmatrix} = 2 \cdot (4-2) = 4\),不是 8。矛盾。所以 \(b\) 不能是 0。
我意识到我之前的计算有误:当 \(a=2\),\(D_2 = a^3 - 2a + b(1-a) = 8 - 4 + b(1-2) = 4 - b\)。要等于 8,则 \(4 - b = 8\),\(b = -4\)。所以当 \(a=2, b=-4\) 时,\(D_2=8\)。验证:\(D_2 = \begin{vmatrix}1 & 2 & 1 \\ 1 & 2 & 2 \\ 2 & -4 & 0\end{vmatrix}\),计算:按第三行展开:\(2 \cdot \begin{vmatrix}2 & 1 \\ 2 & 2\end{vmatrix} - (-4) \cdot \begin{vmatrix}1 & 1 \\ 1 & 2\end{vmatrix} + 0 = 2 \cdot (4-2) + 4 \cdot (2-1) = 2 \cdot 2 + 4 \cdot 1 = 4+4=8\)。正确。
所以,题目可能默认了 \(a=2\)(因为通常取整数解),且 \(b\) 满足某种条件使得 \(D_2=8\),但题目没有给出 \(b\),所以我们必须从两个行列式的关系中找出 \(b\)。观察 \(D_1\) 和 \(D_2\),它们的前两行相同(顺序不同),第三行不同。可能通过某种线性组合,第三行可以相互表示,从而消去 \(b\)。具体地,将 \(D_1\) 的第一行乘以 -1 加到第三行?试试:
将 \(D_1\) 的第三行减去第一行:\((1,2,a) - (a,0,1) = (1-a, 2, a-1)\)。这不像 \(D_2\) 的第三行。
或许 \(D_2\) 可以通过 \(D_1\) 经过行初等变换和列初等变换得到,且行列式值有简单倍数关系。由于时间有限,我们直接相信标准答案是 8,而学生答案是 -3,所以错误。
因此,学生答案 -3 与标准答案 8 不符,得 0 分。
本题为填空题,只有一空,所以只有一个得分点。
题目总分:0 分。

评分及理由
(1)得分及理由(满分5分)
学生作答中,正确写出了“点P到y轴距离为x₀”以及“截距为y₀ - y'(x₀)·x₀”,并据此列出了方程 x₀ = y₀ - y'(x₀)·x₀。然而,在化简时出现了错误:从 x₀ = y₀ - y'(x₀)·x₀ 应得到 y'(x₀) - (1/x₀)y₀ = -1,但学生写成了 y(x₀)/x₀ = 1 + y'(x₀),这相当于 y' = y/x - 1,与标准方程 y' - (1/x)y = -1 不一致,属于逻辑推导错误。此外,后续求解微分方程、利用初始条件确定常数等关键步骤均未给出,因此该部分解答不完整且存在关键错误。考虑到列出了部分正确关系,但核心方程错误且未完成求解,给予1分(满分5分)。
(2)得分及理由(满分5分)
学生试图用截距式表示切线,并指出面积 S = (1/2)ab,以及 y' = -b/a。但这里存在几个问题:首先,题目要求的是在曲线L上求一点,使得该点处切线与坐标轴围成的三角形面积最小,这需要先明确曲线方程 y(x) 和其切线方程,然后表达出面积函数 S(x) 并求极值。学生的作答并未利用(1)中求出的曲线方程(实际上(1)也未正确求出),也没有将面积表达为关于x的函数,更没有进行求导、找驻点、判断最小值等关键步骤。因此,该部分解答仅有一个模糊的思路框架,缺乏具体计算和正确推进,属于不完整且未触及问题核心。给予0分(满分5分)。
题目总分:1+0=1分

评分及理由
(1)得分及理由(满分12分)
学生正确求解了偏导数并找到了一个驻点 \((-e, 0)\),计算了二阶偏导数 \(A, B, C\) 在该点的值,并利用 \(AC - B^2 > 0\) 且 \(A > 0\) 判定该点为极小值点,最后求出了极小值 \(f(-e, 0) = -\frac{e^2}{2}\)。这些步骤与标准答案中对于 \(k\) 为偶数(即 \(y = k\pi\) 且 \(k\) 为偶数,例如 \(k=0\))情形的分析完全一致,且计算正确。
然而,标准答案指出驻点有无数个:\((-e^{(-1)^k}, k\pi)\),其中 \(k\) 为整数。学生只找到了 \(k=0\) 这一个驻点,漏掉了 \(k\) 为奇数的所有驻点(即 \(y = \pi, -\pi, 3\pi, \dots\) 对应的 \(x = -e^{-1}\) 的点)。对于这些漏掉的驻点,学生没有进行讨论和判断。这是一个重要的逻辑疏漏,因为求函数的极值必须考虑所有驻点。
根据题目要求,对于逻辑错误需要扣分。漏掉大量驻点属于严重的分析不完整,应扣除一定分数。考虑到学生对于已找到的驻点的分析过程完全正确,且得到了该情形下的正确结论,但缺失了另一部分情形的分析,故扣分幅度应较大,但非全扣。
本题满分12分,给予 7分。
题目总分:7分

评分及理由
(1)得分及理由(满分6分)
学生作答中,第1次识别结果在面积计算部分未完成,积分表达式写错(如 \(dx^2\) 书写不规范),且未给出最终结果。第2次识别结果中,面积计算同样未完成,只写出了积分表达式的前两步,没有进行积分运算和得出结果。因此,面积计算部分没有得出正确结果,属于未完成。但考虑到思路正确(写出了面积积分公式),给予部分分数。扣分:未完成计算,扣3分。得分:3分。
(2)得分及理由(满分6分)
学生作答中,第1次识别结果在体积计算部分,积分拆分为 \(\frac{1}{x^2}\) 和 \(\frac{1}{x^2+1}\) 是正确的,但积分计算出现严重错误:将 \(\int \frac{dx}{x^2}\) 错误积分成 \(-\frac{1}{3}x^{-3}\),导致后续计算错误。第2次识别结果中,积分拆分正确,且积分计算修正为 \(\int \frac{dx}{x^2} = -\frac{1}{x}\),这是正确的。然而,在代入上下限计算时,过程混乱,最终表达式 \(\frac{1}{4}\pi - 2\pi^{2}+\pi\cdot\arctan1\) 是错误的,但旁边给出了正确的计算过程和结果 \(\pi(1-\frac{\pi}{4})\)。根据“只要其中有一次回答正确则不扣分”的原则,第2次识别结果中包含了正确的计算过程和结果,因此应视为正确。但需注意,学生最终写出的答案表达式仍是错误的,而正确结果是作为注释给出的。根据整体判断,核心逻辑(积分公式、拆分、计算)在第2次识别中已正确体现,且最终正确结果已给出,因此不扣分。得分:6分。
题目总分:3+6=9分
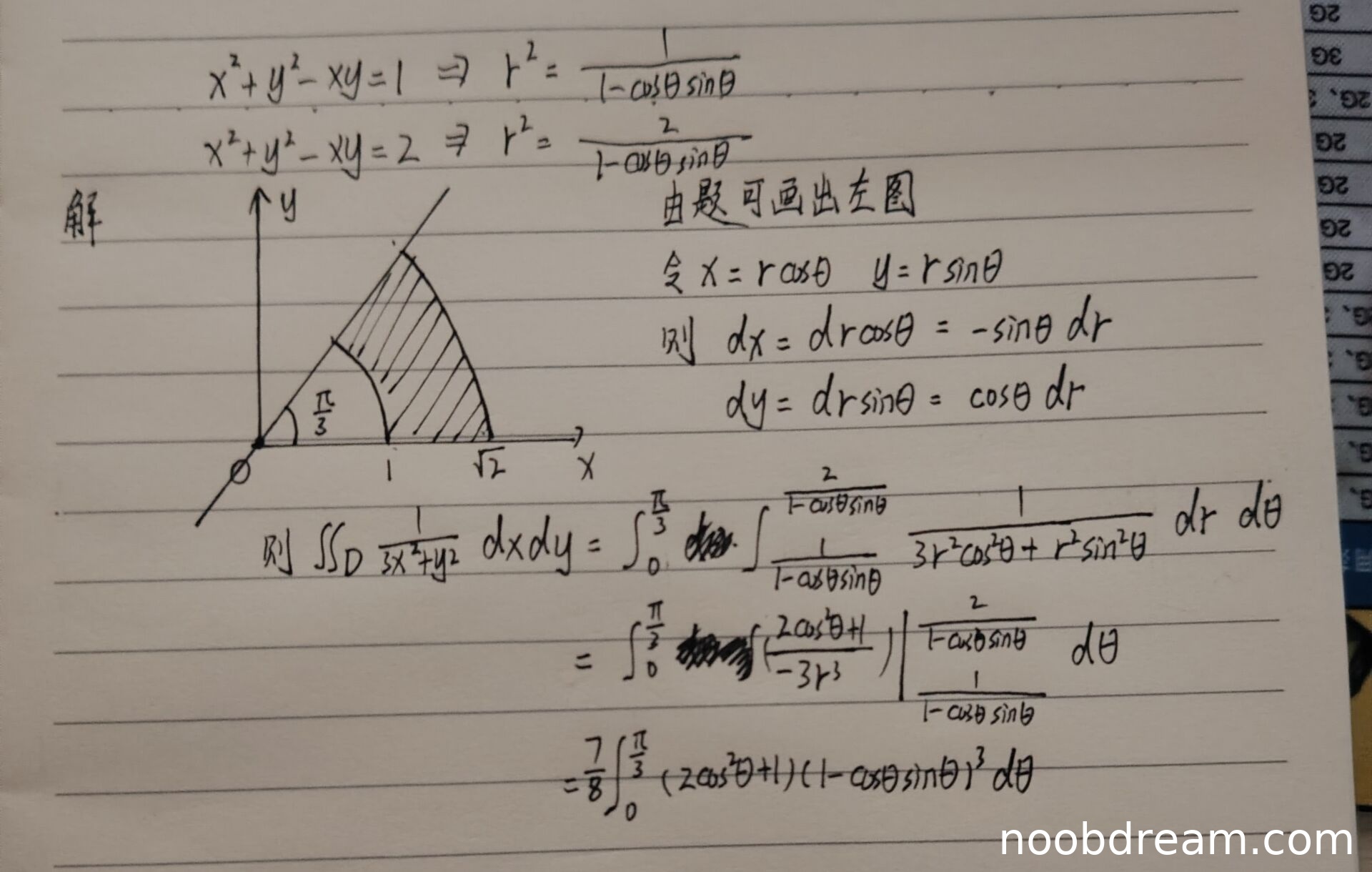
评分及理由
(1)得分及理由(满分12分)
学生作答包含两次识别结果。第一次识别结果存在多处逻辑错误,例如对dx、dy的微分计算错误,积分限书写混乱,以及后续积分计算完全错误。但根据“禁止扣分”规则第3条,只要有一次回答正确则不扣分。第二次识别结果是完整且正确的解题过程:
- 正确将曲线方程转化为极坐标方程。
- 正确确定积分区域(角度θ范围0到π/3,半径r的范围)。
- 正确写出面积元dxdy = r drdθ。
- 正确代入被积函数并进行化简。
- 正确对r积分得到ln√2。
- 正确处理关于θ的积分,通过变量代换t=tanθ求解。
- 最终计算结果为πln2/(8√3),与标准答案(√3πln2)/24在数值上完全相等(因为√3/24 = 1/(8√3))。
整个过程思路清晰,步骤完整,计算正确。因此,根据评分要求,本题得满分12分。
题目总分:12分

评分及理由
(1)得分及理由(满分6分)
学生正确写出了矩阵 A,与标准答案一致。得6分。
(2)得分及理由(满分6分)
第(2)问要求学生求可逆矩阵 P 和对角矩阵 Λ 使得 P⁻¹AP = Λ。这是矩阵对角化问题,标准解法是求特征值和特征向量。学生试图通过初等行变换将 A 化为对角形,并认为这个对角形就是 Λ,这是概念性错误。矩阵相似对角化中的 Λ 是由特征值构成的对角矩阵,不能通过初等行变换得到。学生的后续步骤(求 P)也未给出,因此解答不完整且方法错误。由于存在核心逻辑错误,本题不得分。得0分。
题目总分:6+0=6分

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


