
科目组合
计算机: 数据结构 、计算机组成原理 、操作系统 、计算机网络
答题情况分析报告
1):定义三个下标分别表示s1,s2,s3当前遍历下标,然后定义sum=|a-b|+|b-c|+|c-a|,以及minnum=sum,mini=i,minj=j,mink=k;(a∈S1,b∈S2,c∈S3)初始值为INT_MAX;接着我们怎么将s1[i],s2[j],s3[k]中最小值的下标加一,比较当前sum与minnum的大小如果minnum<sum则进行更新mini,minj,mink否则继续上面操作,直到
i==s1.length,j=s2.length,k=s3.length;
2):
// 全局变量(注意:在多线程或多次调用时可能有副作用,建议改为局部变量+返回结构体)
6int sum = INT_MAX;
7int minnum = INT_MAX; // 初始最小值设为最大整数
8int mini = 0;
9int minj = 0;
10int mink = 0;
11
12/**
13 * 辅助函数:返回三个整数中的最小值
14 */
15int min3(int a, int b, int c) {
16 int min_val = a;
17 if (b < min_val) min_val = b;
18 if (c < min_val) min_val = c;
19 return min_val;
20}
21
22/**
23 * 函数功能:
24 * 在三个**已升序排序**的整型数组 s1, s2, s3 中,
25 * 寻找下标 (i, j, k),使得三元组 (s1[i], s2[j], s3[k]) 的
26 * 两两绝对差之和最小:
27 * |s1[i] - s2[j]| + |s2[j] - s3[k]| + |s3[k] - s1[i]|
28 *
29 * 参数:
30 * s1, s2, s3 —— 三个已排序的数组
31 * len1, len2, len3 —— 各自的长度
32 */
33void minlenth(int s1[], int s2[], int s3[], int len1, int len2, int len3) {
34 int i = 0, j = 0, k = 0; // 三个指针,初始都指向各自数组开头
35
36 // 循环条件:只要有一个指针越界就停止(避免访问非法内存)
37 while (i < len1 && j < len2 && k < len3) {
38 // 计算当前三元组的距离总和
39 sum = abs(s1[i] - s2[j]) + abs(s2[j] - s3[k]) + abs(s3[k] - s1[i]);
40
41 // 如果当前总和更小,更新全局最小值和对应下标
42 if (sum < minnum) {
43 minnum = sum;
44 mini = i;
45 minj = j;
46 mink = k;
47 }
48
49 // 找出当前三个元素中的最小值
50 int current_min = min3(s1[i], s2[j], s3[k]);
51
52 // 贪心策略:将指向最小值的指针前移,以尝试缩小差距
53 if (s1[i] == current_min) {
54 i++;
55 } else if (s2[j] == current_min) {
56 j++;
57 } else {
58 k++;
59 }
60 }
61
62 // 输出结果(注意:应输出 minnum,不是 sum)
63 printf("最小总距离: %d\n", minnum);
64 printf("对应的下标: (%d, %d, %d)\n", mini, minj, mink);
65 printf("对应的元素: (%d, %d, %d)\n", s1[mini], s2[minj], s3[mink]);
66}
67
3):时间复杂度是o(n),空间复杂度是o(1);
评分及理由
(1)得分及理由(满分3分)
学生给出了算法的基本设计思想:使用三个指针分别遍历三个数组,每次移动指向最小元素的指针,并计算当前三元组的距离,更新最小值。这一思路与标准答案中的“同向多指针(滑动窗口变体)”方法一致,是正确的。但描述中“直到 i==s1.length,j=s2.length,k=s3.length”存在歧义(应为三个指针中任意一个到达末尾即终止),且未明确说明循环终止条件。由于核心思想正确,但表述不够严谨,扣1分。
得分:2分
(2)得分及理由(满分8分)
学生用C语言实现了算法,关键部分有注释,整体结构清晰。但存在以下逻辑错误和问题:
1. 代码中使用了全局变量(sum、minnum等),这会导致函数不可重入,且题目要求输出最小距离,而函数直接打印结果,不符合通常的函数设计规范(应返回最小距离值)。
2. 在指针移动策略中,使用`min3`函数找出当前三个元素的最小值,然后移动指向该最小值的指针。这一策略在多数情况下有效,但存在缺陷:当有多个指针指向相同的最小值时,只移动其中一个指针(代码中按顺序判断,先移动s1的指针),可能导致错过某些三元组。例如,若s1[i]和s2[j]相等且均为最小值,代码会移动i而固定j,这可能导致最优解被跳过。标准答案通过比较三个值的大小关系来移动指针,避免了这一问题。
3. 循环结束后,输出结果时直接使用全局变量minnum和下标,但若输入数组长度为零(题目已说明非空,可忽略),或从未更新minnum(初始为INT_MAX),则输出可能不正确。但根据题目数据,此问题不影响结果。
4. 函数名为`minlenth`,但未返回最小距离值,不符合算法题通常要求返回结果的惯例。
基于以上逻辑错误,尤其是第2点指针移动策略的缺陷,扣3分。
得分:5分
(3)得分及理由(满分2分)
学生正确说明了时间复杂度为O(n)(即O(n1+n2+n3)),空间复杂度为O(1)。但未具体说明n的含义。由于分析正确,不扣分。
得分:2分
题目总分:2+5+2=9分
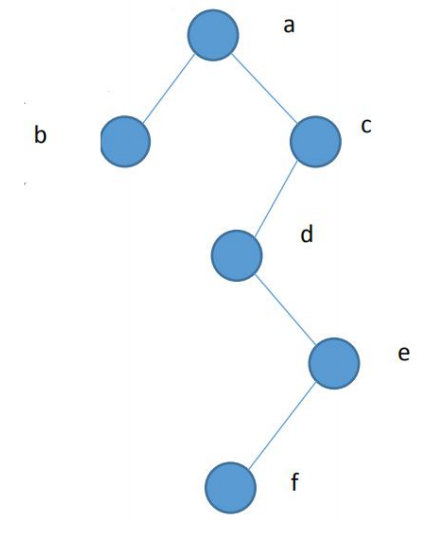
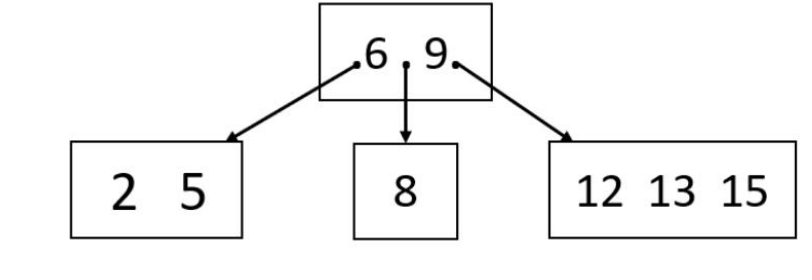
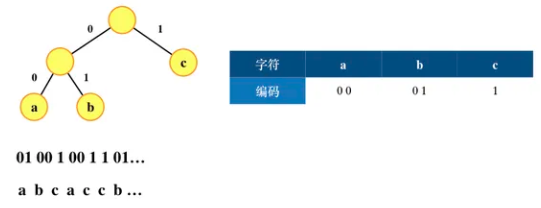
1):哈夫曼树
2):从树根到叶子结点从上到下,遇到分支结点向左走标注0,向右走标注1,直到到达了叶子结点为止;
3):根据遍历某个字符编码从根结点开始如果遇到0就向左走或者构造左孩子结点;遇到1就向右走后者构造右孩子结点,
如果遍历完成后仍然是在非终端结点,那么就是前缀特性,或者没有遍历完成到达了叶子结点,也是前缀特性;
否则就不具备前缀特性;
评分及理由
(1)得分及理由(满分4分)
学生回答“哈夫曼树”,这本质上是正确的,因为哈夫曼树是前缀编码的一种典型二叉树实现。数据结构应更准确地表述为“二叉树”或“哈夫曼树/前缀编码树”。考虑到“哈夫曼树”直接对应了前缀编码的常用数据结构,且题目并未要求更具体的名称,故给满分。
得分:4分
(2)得分及理由(满分3分)
学生描述了从根到叶子的路径遍历过程,并说明了根据0/1选择左/右分支,直到叶子结点。这基本描述了译码的单字符解码过程。但译码过程是针对整个0/1串,需要反复从根开始,直到处理完所有输入。学生答案只描述了解一个字符的过程,未明确“重复此过程”或“处理整个串”,表述不完整。
扣1分。
得分:2分
(3)得分及理由(满分3分)
学生描述了根据编码构造树的过程,但判断逻辑表述存在严重错误。学生说“如果遍历完成后仍然是在非终端结点,那么就是前缀特性,或者没有遍历完成到达了叶子结点,也是前缀特性”,这与前缀特性的定义相悖。前缀特性要求任何字符的编码不能是另一个字符编码的前缀,因此编码必须对应到叶子结点,且构造过程中不能重复使用或提前到达已有字符的结点。学生的判断条件恰好说反了(到达叶子结点说明可能是其他编码的前缀,不具备前缀特性)。逻辑错误,扣3分。
得分:0分
题目总分:4+2+0=6分
1):乘法指令可以用加法指令和移位指令替代完成;
2):控制逻辑的作用是控制循环次数以及控制移位;
3):没有乘法指令执行时间最长,使用阵列乘法器实现的乘法指令执行的时间最短;
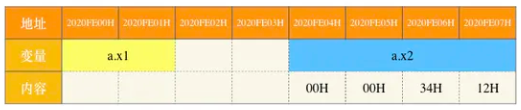
4):两者的结果均是:00 00 00 00 FF FF FF FE,此时函数umul()没有溢出,imul()的返回结果溢出,我们可以根据前n项是否全为0来判断,如果不是则溢出否则不溢出;
评分及理由
(1)得分及理由(满分2分)
学生回答“乘法指令可以用加法指令和移位指令替代完成”,正确指出了乘法运算可以通过加法和移位操作实现,与标准答案核心思想一致。但答案较为简略,未提及“编译器转换”或“循环代码段”等更具体的实现方式。考虑到问题为2分,且核心观点正确,扣1分。得1分。
(2)得分及理由(满分2分)
学生回答“控制逻辑的作用是控制循环次数以及控制移位”,基本正确。标准答案还提到了“根据操作表控制加法和移位操作”,学生的答案“控制移位”可以理解为包含了移位的控制,但未明确提及对“加法”的控制。表述不够完整,扣1分。得1分。
(3)得分及理由(满分4分)
学生回答“没有乘法指令执行时间最长,使用阵列乘法器实现的乘法指令执行的时间最短”,结论完全正确。但缺少对三种情况执行时间差异的具体理由分析,例如未说明①是通过软件模拟、②是通过多周期硬件指令、③是单周期硬件实现等关键区别。因此,结论正确但解释不足,扣2分。得2分。
(4)得分及理由(满分5分)
第一问:学生回答“两者的结果均是:00 00 00 00 FF FF FF FE”。对于无符号乘法,该结果是正确的64位乘积。但对于有符号乘法(imul),标准答案指出其64位乘积的补码表示也是“00000000FFFFFFFEH”,学生答案“两者均是”在数值上正确,但未明确这是补码表示,表述不够严谨,此处不扣分。得2分(此问分值需根据整体分配估算,此处按部分正确给分)。
第二问:学生回答“umul()没有溢出,imul()的返回结果溢出”,判断完全正确。得1分。
第三问:学生回答“我们可以根据前n项是否全为0来判断,如果不是则溢出否则不溢出”,其中“前n项”表述不精确,应为“乘积的高n位”。但核心思想(高n位全0则不溢出,否则溢出)正确。扣1分。得1分。
本小题总计得4分。
题目总分:1+1+2+4=8分
1):标记(Tag):20,LRU位:3位,不需要修改位;
2):64次
3):根据6~11位,来判断该地址是位于cache第0组,访问cache第0组发现cache缺失,于是转向主存查找,读地址的高26位来确定块号,将该块调入cache中并将有效位设置为1,最后将根据后六位确定的快内偏移量将所需内容调入cpu;
评分及理由
(1)得分及理由(满分3分)
学生答案:标记(Tag):20, LRU位:3位, 不需要修改位。
标准答案:标记占20位,LRU位占3位,采用直写方式故没有修改位。
评分:学生答案与标准答案完全一致,且表述清晰。得3分。
(2)得分及理由(满分3分)
学生答案:64次。
标准答案:64次。
评分:答案正确。虽然学生未给出计算过程,但最终结果与标准答案一致。在考试中,若题目仅要求给出最终缺失次数,且答案正确,应给满分。得3分。
(3)得分及理由(满分4分)
学生答案:根据6~11位,来判断该地址是位于cache第0组,访问cache第0组发现cache缺失,于是转向主存查找,读地址的高26位来确定块号,将该块调入cache中并将有效位设置为1,最后将根据后六位确定的快内偏移量将所需内容调入cpu。
标准答案:组号为地址中间6位(第6-11位),计算得0,映射到组0。Cache初始为空,访问缺失。访问主存获取数据送入CPU,同时更新Cache:将主存块存入组0某一行,填入高20位标记,设置有效位,修改LRU位。
评分分析:学生答案基本描述了过程,包括判断组号、发现缺失、访问主存、调入Cache、设置有效位、根据块内偏移取数据。但存在两处不准确或错误: 1. “读地址的高26位来确定块号”:此描述错误。主存地址高20位是标记(Tag),用于与Cache行中的标记比较以判断是否命中,并非“块号”。主存块地址由“标记+组号”构成(或理解为高26位是主存块地址,但标准描述中更强调“标记”字段的作用)。此表述不严谨,可能引起混淆。 2. 遗漏了更新“LRU位”这一关键步骤。 由于存在一处关键描述错误(高26位为块号)和一处遗漏(LRU位更新),需扣分。
扣分:本题满分4分。描述中存在实质性错误(主存地址高26位的作用描述不当)扣1分,遗漏LRU位更新扣1分。得2分。
题目总分:3+3+2=8分
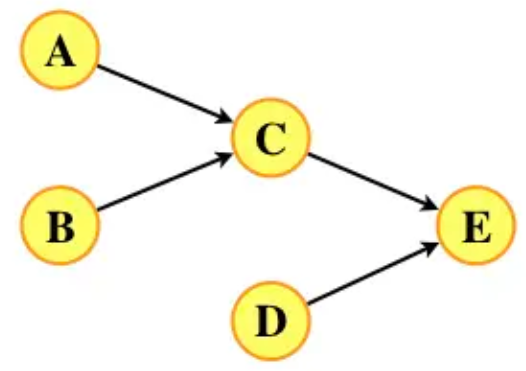
Semaphore AC=0,BC=0,CE=0,DE=0;//确定C与A和B,E与C和D同步信号量机制;
PA(){
//执行操作A
signal(AC);
}
PB(){
//执行操作B
signal(BC);
}
PC(){
wait(AC);
wait(BC);
//执行操C
signal(CE);
}
PD(){
//执行操作D;
signal(DE)
}
PE(){
wait(CE);
wait(DE):
//执行操作E
}
评分及理由
(1)得分及理由(满分7分)
学生答案与标准答案在核心逻辑上完全一致:
- 正确定义了四个信号量AC、BC、CE、DE,并正确地将初值设为0。
- 在进程A和B中,分别执行操作后signal(AC)和signal(BC),正确释放了C的等待条件。
- 在进程C中,通过wait(AC)和wait(BC)确保A和B都完成后才执行C,执行后signal(CE)通知E。
- 在进程D中,执行操作后signal(DE)通知E。
- 在进程E中,通过wait(CE)和wait(DE)确保C和D都完成后才执行E。
因此,该答案正确实现了题目要求的同步关系。虽然代码在格式和个别标点符号(如PD中的中文括号、PE中wait(DE)后的冒号)上存在笔误,但这些并不影响同步逻辑的正确性,属于非关键性书写错误,不扣分。
得分:7分。
题目总分:7分
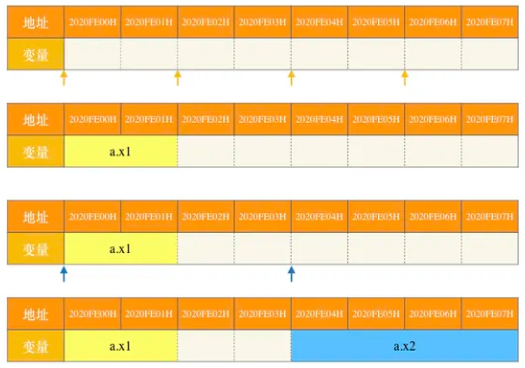
1):a[1][2]的虚拟地址是1080 0000H+4*(1024+2)=1080 0000H+1008H=10801008H
页目录号:00 0100 0010=042H,页号: 000 0000 000=000H
对应的页目录项的物理地址是 0020 1000H
页表项的物理地址是:00301008H
2):数组a在虚拟地址空间中所占区域是连续的,在物理地址空间中所占区域不一定连续;
3):对数组进行按行存储会更好;
评分及理由
(1)得分及理由(满分4分)
① 虚拟地址计算正确,得1分。
② 页目录号计算正确(042H),得0.5分;页号计算错误(应为001H,学生答000H),扣0.5分。
③ 页目录项物理地址计算错误(应为0020 1000H+4×042H=0020 1108H,学生直接给出页目录起始地址),扣1分。
④ 页表项物理地址计算错误(应为00301H<<12 + 4×001H = 00301004H,学生计算为00301008H),扣1分。
本小题共扣2.5分,得1.5分。
(2)得分及理由(满分2分)
① 虚拟地址空间必须连续,回答正确,得1分。
② 物理地址空间不必连续,回答正确,得1分。
本小题得2分。
(3)得分及理由(满分2分)
回答“按行存储会更好”,虽然表述不精确(应为“按行遍历”),但意思正确,得2分。
题目总分:1.5+2+2=5.5分
1):需要进行R3NAT转换表
203.10.2.6 80 192.168.1.2 80
203.10.2.6 80 192.168.1.3 80
2):源 IP 地址:192.168.1.2,目的 IP 地址:203.10.2.2
经过 R3 转发后,P 的源 IP 地 址和目的 IP 地址分别是203.10.2.6,203.10.2.2
经过 R2 转发后,P 的源 IP 地址和目的 IP 地址分别是203.10.2.6 192.168.1.2
评分及理由
(1)得分及理由(满分3分)
学生回答需要进行R3的NAT转换表配置,并给出了具体的转换条目。标准答案要求配置在路由器R2上,因为R2是连接内网(192.168.1.0/24)和外网(203.10.2.0/24)的边界路由器,NAT功能通常在边界路由器上启用。学生将NAT配置在R3上,R3是连接两个局域网(192.168.1.0/24和192.168.2.0/24)的内部路由器,这不符合典型的网络拓扑和NAT部署原则。虽然学生给出的转换表内容(IP和端口映射)本身是正确的,但配置位置错误,这是一个关键的逻辑错误。因此扣2分,得1分。
(2)得分及理由(满分6分)
学生回答的H2发送P时的源IP和目的IP完全正确,得2分。
学生回答的经过R3转发后的源IP和目的IP完全正确,得2分。
学生回答的经过R2转发后的源IP和目的IP完全正确,得2分。
该部分答案与标准答案一致,没有错误,因此得满分6分。
题目总分:1+6=7分
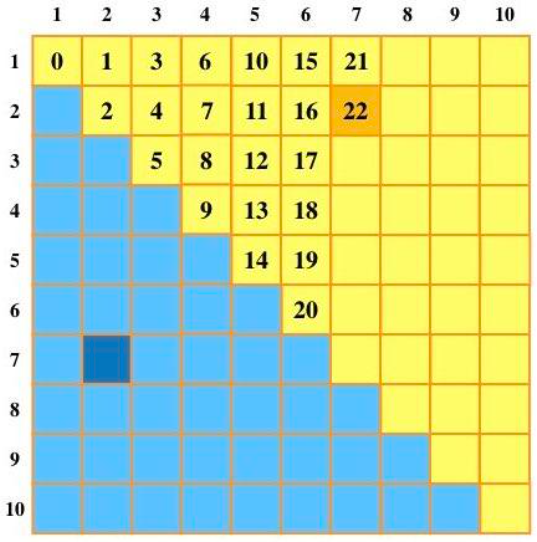



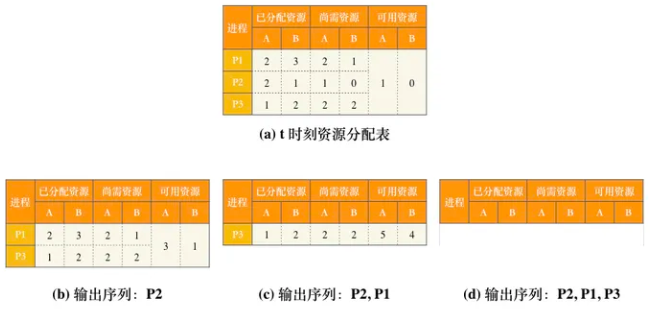


 。主存块大小为64B= 2^6B,按字节编址,主存地址低6位为块内地址,数据区容量各为32KB,行数为32KB/64B=2^9,采用8路组相联,组数为2^9/8=2^6,主存地址中间6位为Cache组号,主存地址为32位,主存地址中高32-6-6=20位为标记,8路组相联LRU位占 log8=3 位,采用直写方式,故没有修改位。
。主存块大小为64B= 2^6B,按字节编址,主存地址低6位为块内地址,数据区容量各为32KB,行数为32KB/64B=2^9,采用8路组相联,组数为2^9/8=2^6,主存地址中间6位为Cache组号,主存地址为32位,主存地址中高32-6-6=20位为标记,8路组相联LRU位占 log8=3 位,采用直写方式,故没有修改位。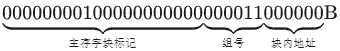 ,块内地址为000000B=0,所以s位于一个主存块开始处,需要访问1024个数组元素,每个数组元素类型为int,占4B,主存块大小为64B,1024个数组元素占1024×4B/64B=64个主存块。执行程序段过程中,观察s[k]=2*s[k],每个数组元素都需要读、写各1次,主存块大小为64B,每访问一个主存块(包含64B/4B=16个数组元素)产生一次Cache缺失,每个主存块会访问16×(1+1)=32次。总共需要访问64个主存块,产生64×1=64次Cache缺失。所以该程序段执行过程中,访问数组s的数据Cache缺失次数为64。
,块内地址为000000B=0,所以s位于一个主存块开始处,需要访问1024个数组元素,每个数组元素类型为int,占4B,主存块大小为64B,1024个数组元素占1024×4B/64B=64个主存块。执行程序段过程中,观察s[k]=2*s[k],每个数组元素都需要读、写各1次,主存块大小为64B,每访问一个主存块(包含64B/4B=16个数组元素)产生一次Cache缺失,每个主存块会访问16×(1+1)=32次。总共需要访问64个主存块,产生64×1=64次Cache缺失。所以该程序段执行过程中,访问数组s的数据Cache缺失次数为64。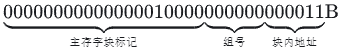 ,根据主存地址划分可知,组号为000000B=0,故该地址所在主存块被映射到指令Cache组0。因为Cache初始为空,所有Cache行的有效位均为0,所以Cache访问缺失。此时,直接按地址访问主存,将获取到的数据直接送入CPU,同时更新Cache,将目标数据所在主存块取出后存入指令Cache组0的某一行,并将主存地址高20位填入该行标记字段,设置有效位,修改LRU位。
,根据主存地址划分可知,组号为000000B=0,故该地址所在主存块被映射到指令Cache组0。因为Cache初始为空,所有Cache行的有效位均为0,所以Cache访问缺失。此时,直接按地址访问主存,将获取到的数据直接送入CPU,同时更新Cache,将目标数据所在主存块取出后存入指令Cache组0的某一行,并将主存地址高20位填入该行标记字段,设置有效位,修改LRU位。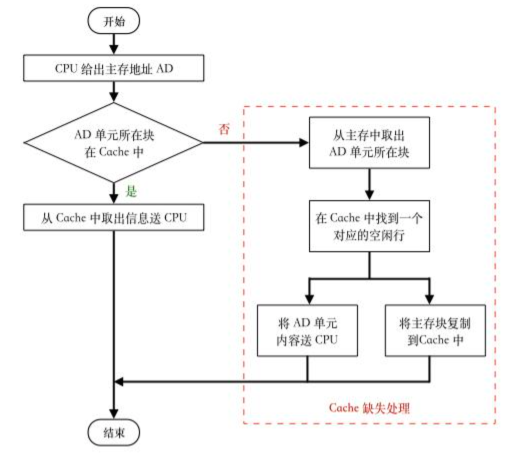


 ,对应的页目录号是0001000010B=042H,页号是00 0000 0001B=001H。
,对应的页目录号是0001000010B=042H,页号是00 0000 0001B=001H。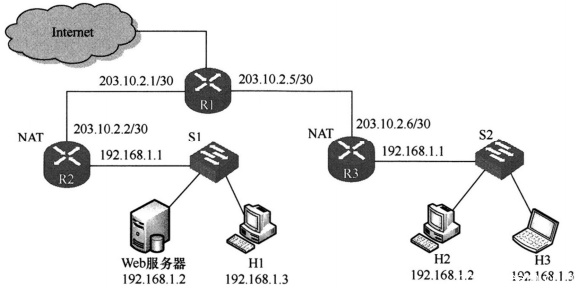



 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


