
2026年(408)计算机学科专业基础综合试题
科目组合
计算机: 数据结构 、计算机组成原理 、操作系统 、计算机网络
00:
05:
37
答题卡
得分 64/150
答对题目数 32/47
评价
☆☆☆☆☆
答题情况分析报告
正确: 32
错误: 15
未答: 0
总分: 64/150
正确率 68.1%
第1题
题目链接
正确答案:A
你的答案:
正确
正确率:0%
点击此处查看本题答案
第2题
题目链接
正确答案:D
你的答案:
B
正确率:0%
点击此处查看本题答案
第3题
题目链接
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
第4题
题目链接
正确答案:B
你的答案:
D
正确率:0%
点击此处查看本题答案
第5题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第6题
题目链接
正确答案:D
你的答案:
C
正确率:0%
点击此处查看本题答案
第7题
题目链接
正确答案:B
你的答案:
正确
正确率:0%
点击此处查看本题答案
第8题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第9题
题目链接
正确答案:B
你的答案:
正确
正确率:0%
点击此处查看本题答案
第10题
题目链接
正确答案:A
你的答案:
正确
正确率:0%
点击此处查看本题答案
第11题
题目链接
正确答案:C
你的答案:
D
正确率:0%
点击此处查看本题答案
第12题
题目链接
正确答案:C
你的答案:
D
正确率:0%
点击此处查看本题答案
第13题
题目链接
正确答案:A
你的答案:
正确
正确率:0%
点击此处查看本题答案
第14题
题目链接
正确答案:B
你的答案:
正确
正确率:0%
点击此处查看本题答案
第15题
题目链接
正确答案:A
你的答案:
正确
正确率:0%
点击此处查看本题答案
第16题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第17题
题目链接
正确答案:B
你的答案:
正确
正确率:0%
点击此处查看本题答案
第18题
题目链接
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
第19题
题目链接
正确答案:A
你的答案:
D
正确率:0%
点击此处查看本题答案
第20题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第21题
题目链接
正确答案:D
你的答案:
B
正确率:0%
点击此处查看本题答案
第22题
题目链接
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
第23题
题目链接
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
第24题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第25题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第26题
题目链接
正确答案:A
你的答案:
正确
正确率:0%
点击此处查看本题答案
第27题
题目链接
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
第28题
题目链接
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
第29题
题目链接
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
第30题
题目链接
正确答案:B
你的答案:
正确
正确率:0%
点击此处查看本题答案
第31题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第32题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第33题
题目链接
正确答案:B
你的答案:
正确
正确率:0%
点击此处查看本题答案
第34题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第35题
题目链接
正确答案:D
你的答案:
正确
正确率:0%
点击此处查看本题答案
第36题
题目链接
正确答案:B
你的答案:
正确
正确率:0%
点击此处查看本题答案
第37题
题目链接
正确答案:B
你的答案:
正确
正确率:0%
点击此处查看本题答案
第38题
题目链接
正确答案:A
你的答案:
正确
正确率:0%
点击此处查看本题答案
第39题
题目链接
正确答案:C
你的答案:
正确
正确率:0%
点击此处查看本题答案
第40题
题目链接
正确答案:D
你的答案:
A
正确率:0%
点击此处查看本题答案
第41题
题目链接
你的答案:
未作答
点击此处查看本题答案
第42题
题目链接
你的答案:
未作答
点击此处查看本题答案
第43题
题目链接
你的答案:
未作答
点击此处查看本题答案
第44题
题目链接
你的答案:
未作答
点击此处查看本题答案
第45题
题目链接
你的答案:
未作答
点击此处查看本题答案
第46题
题目链接
你的答案:
未作答
点击此处查看本题答案
第47题
题目链接
你的答案:
未作答
点击此处查看本题答案
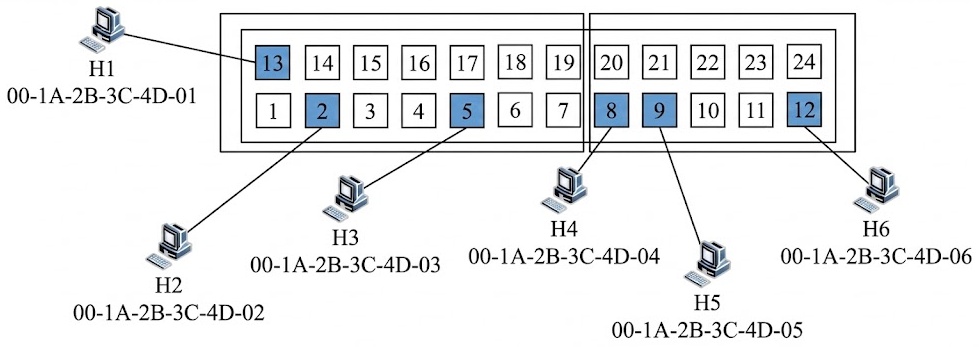
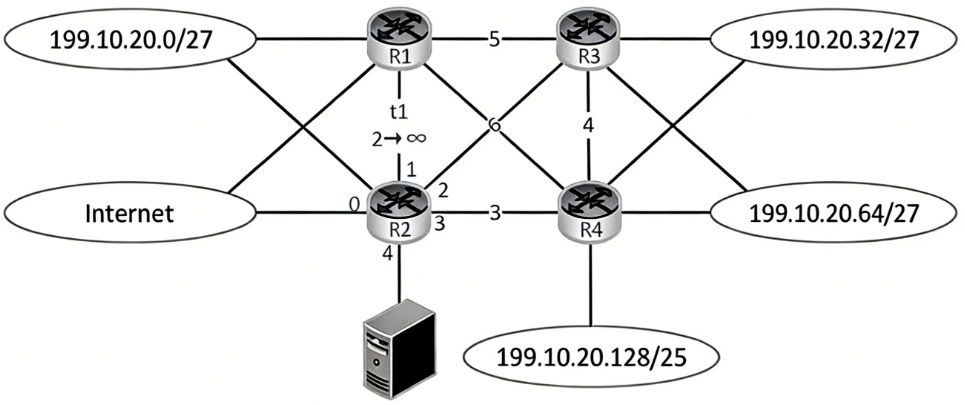
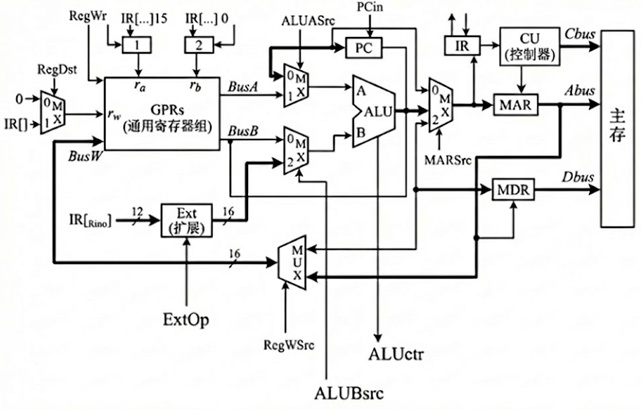
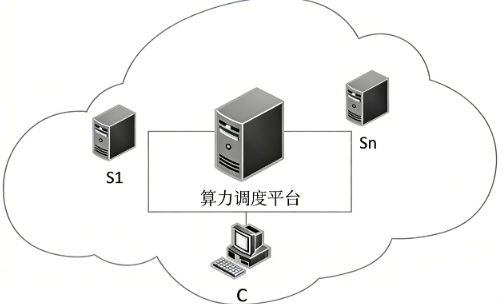

 The road of your choice, you have to go on !
粤ICP备16082171号-1
The road of your choice, you have to go on !
粤ICP备16082171号-1


