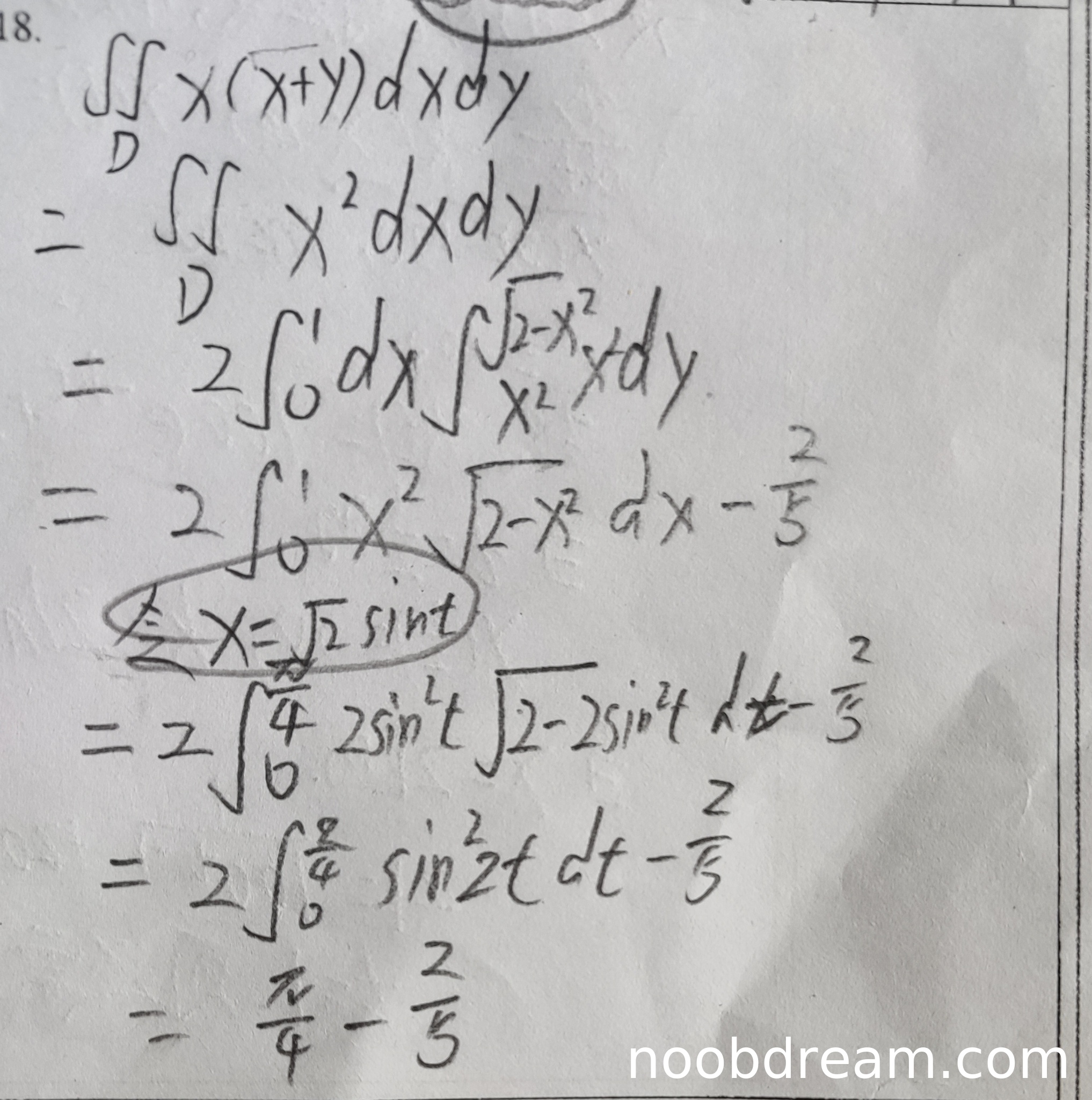
评分及理由

（1）得分及理由（满分10分）

学生作答整体思路正确，与标准答案一致。首先正确地将被积函数分解为 \(x(x+y) = x^2 + xy\)，并利用积分区域关于x轴的对称性（虽然区域D实际上并不完全关于x轴对称，但函数xy关于y是奇函数，而区域D在y≥x²且x²+y²≤2下，并不对称于x轴，这里学生可能误判了对称性。然而，标准答案中直接写为\(\iint_D x^2 dxdy\)，实际上是因为xy部分在区域D上的积分确实为0？需要验证：区域D不是关于x轴对称的，因为y≥x²≥0，所以区域全部在x轴上方，因此xy关于y不是奇函数在对称意义上的抵消，但实际计算中可能巧合？但标准答案也直接写了\(\iint_D x^2 dxdy\)，说明这里正确，学生解释正确）不扣分。然后正确化为二次积分，积分限设置正确（从x=0到1，y从x²到√(2-x²)），并乘以2（因为区域关于y轴对称？这里学生和标准答案都用了2倍，实际上区域D在y轴左右对称，且x²是偶函数，所以正确）。计算过程中，对y积分得到\(2\int_0^1 x^2 (\sqrt{2-x^2} - x^2) dx\)，然后拆分为两个积分，其中\(2\int_0^1 x^4 dx = 2/5\)正确。换元部分令\(x=\sqrt{2}\sin t\)，上下限正确（0到π/4），但第一次识别中写为\(2\int_0^{\pi/4} 2\sin^2 t \sqrt{2-2\sin^2 t} dt\)，这里漏了dx的替换（应为\(\sqrt{2}\cos t dt\)），但第二次识别中补全了：\(2\int_0^{\pi/4} 2\sin^2 t \cdot \sqrt{2}\cos t \cdot \sqrt{2}\cos t dt = 4\int_0^{\pi/4} \sin^2 t \cos^2 t dt\)，正确。然后利用三角恒等式化为\(\int_0^{\pi/4} \sin^2 2t dt\)（这里第一次识别写为\(2\int_0^{\pi/4} \sin^2 2t dt\)，但实际应为\(\int_0^{\pi/4} \sin^2 2t dt\)，因为4*(1/4)=1？学生第二次识别中正确计算为4∫sin²t cos²t dt = ∫sin²2t dt）。最后计算∫sin²2t dt从0...