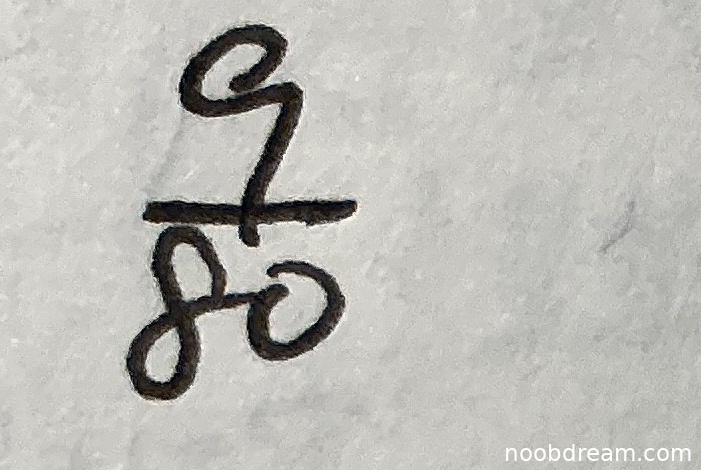
评分及理由

（1）得分及理由（满分5分）

学生第一次识别结果为\(\frac{9}{80}\)，第二次识别结果为\(\frac{97}{80}\)。标准答案为\(\frac{9}{10}\)。两次识别结果均与标准答案不符。

本题需使用贝叶斯公式计算条件概率。设事件A为产品实际合格，事件B为两种设备均检验为合格。已知P(A)=0.1（合格率），P(B|A)=0.9×0.9=0.81（设备正确检出率），P(B|A^c)=0.1×0.1=0.01（设备错误检出率）。则所求概率为： \[ P(A|B) = \frac{P(A)P(B|A)}{P(A)P(B|A) + P(A^c)P(B|A^c)} = \frac{0.1 × 0.81}{0.1 × 0.81 + 0.9 × 0.01} = \frac{0.081}{0.081 + 0.009} = \frac{0.081}{0.09} = \frac{9}{10} \] 学生答案\(\frac{9}{80}\)和\(\frac{97}{80}\)均明显错误，且\(\frac{97}{80}>1\)不符合概率值域[0,1]。识别结果无证据表明是字符误写（如9/10误为9/80），故判定为逻辑错误。根据评分规则，逻辑错误扣分，本题得0分。

题目总分：0分