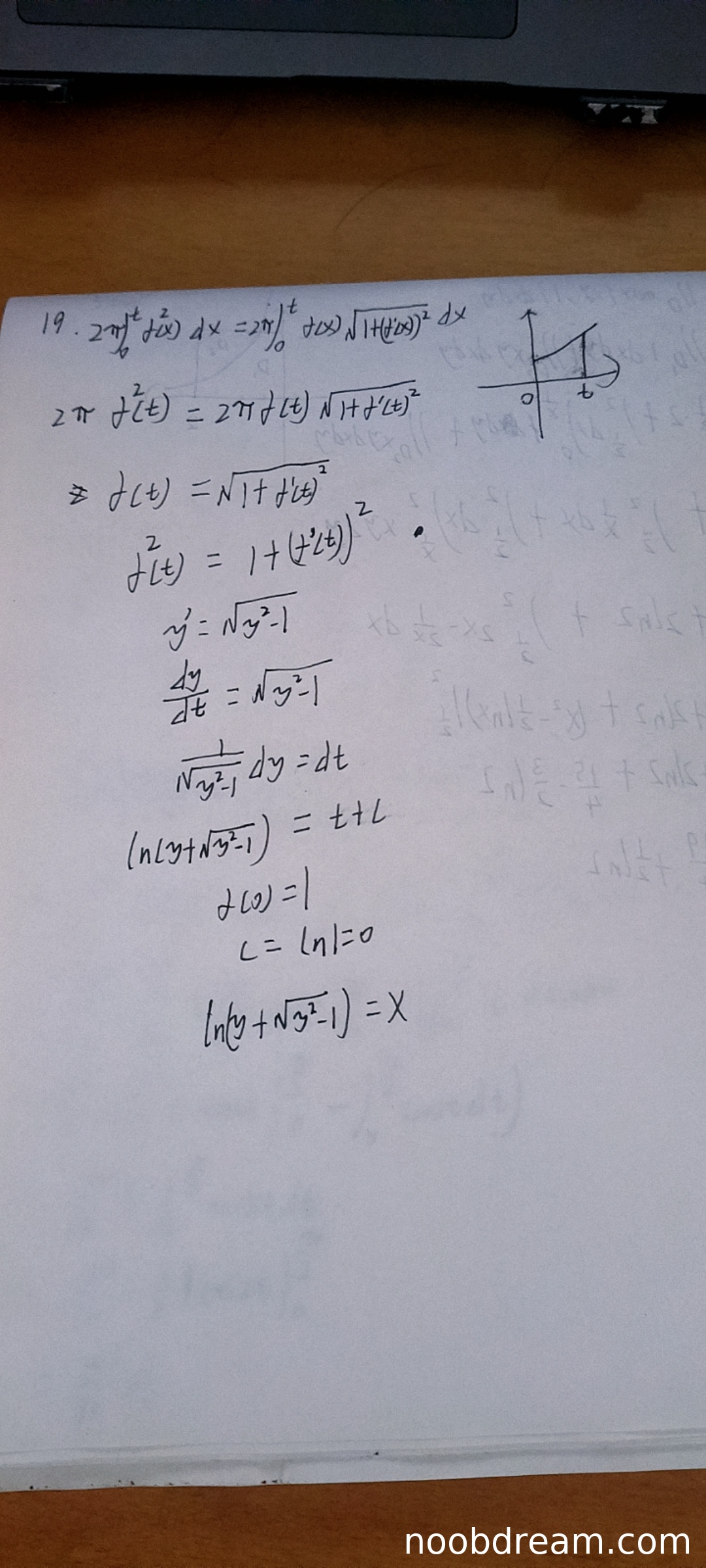
评分及理由

（1）旋转体体积和侧面积表达式（满分2分）

学生第一次识别结果中写出的体积和侧面积表达式有误：体积应为 \(\pi \int_0^t [f(x)]^2 dx\)，但学生写成了 \(2\pi \int_0^t f^2(x) dx\)（多乘了2）；侧面积表达式正确为 \(2\pi \int_0^t f(x)\sqrt{1+[f'(x)]^2} dx\)，但学生写成了 \(2\pi \int_0^t dx\sqrt{1+(f'(x))^2} dx\)（多写了dx且漏了f(x)）。第二次识别结果中侧面积公式描述正确，但体积公式未明确写出。由于核心表达式存在错误，扣1分。

得分：1分（满分2分）

（2）建立方程并求导（满分3分）

学生第一次识别结果中直接写出求导后的方程（跳过了积分方程建立步骤），但方程写错：将 \(S(t)=2V(t)\) 误写为 \(2\pi \int_0^t f^2(x) dx = 2\pi \int_0^t dx\sqrt{1+(f'(x))^2} dx\)（左右颠倒且表达式错误）。第二次识别结果正确建立了积分方程 \(2\pi \int_0^t f(x)\sqrt{1+[f'(x)]^2} dx = 2\pi \int_0^t [f(x)]^2 dx\)（但误写为等号右边是 \(2\pi \int_0^t f(x) dx\)，缺少平方），不过后续求导步骤正确得到 \(f(t)\sqrt{1+[f'(t)]^2} = f(t)\)（但实际应为 \(f(t)\sqrt{1+[f'(t)]^2} = [f(t)]^2\)）。由于第二次识别在求导后通过除以f(t)得到 \(1=\sqrt{1+[f'(t)]^2}\) 是错误的（应得到 \(\sqrt{1+[f'(t)]^2} = f(t)\)），但后续又修正为 \(f'(t)=\sqrt{f^2(t)-1}\)（正确）。考虑到整体思路正确且最终修正了微分方程，扣1分（主要扣分在积分方程建立错误）。

得分：2分（满分3分）

（3）求解微分方程和初始条件应用（满分5分）

学生正确分离变量得到 \(\frac{dy}{\sqrt{y^2-1}} = dt\)，积分得到 \(\ln|y+\sqrt{y^2-1}| = t + C\)，并应用初始条件f(0)=1得到C=0（正确）。最终表达...