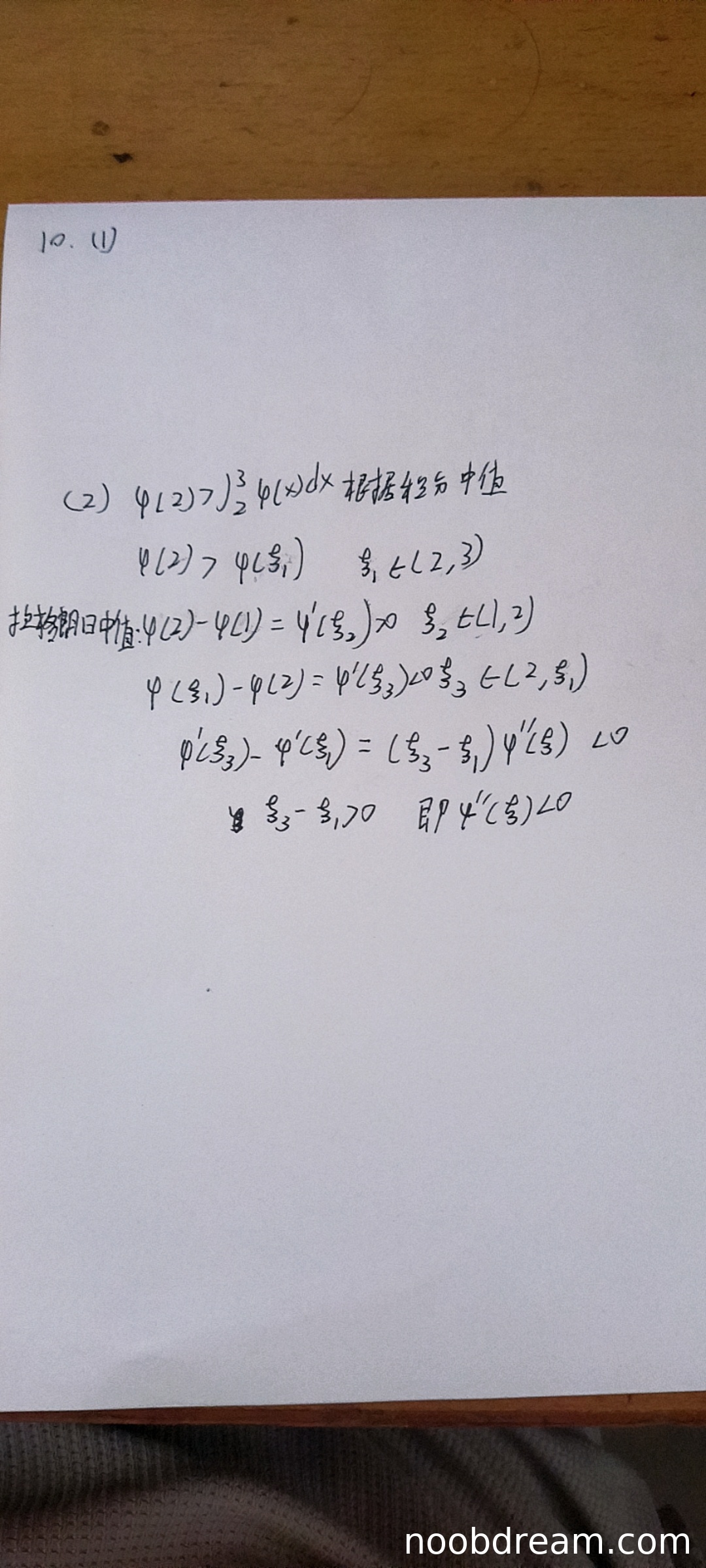
评分及理由

（1）得分及理由（满分5分）

学生未作答第一问（积分中值定理的证明），因此得0分。

（2）得分及理由（满分5分）

学生正确应用了积分中值定理得到存在 \(\xi_1 \in (2,3)\) 使得 \(\int_{2}^{3} \varphi(x) d x=\varphi(\xi_1)\)，并由条件 \(\varphi(2)>\int_{2}^{3} \varphi(x) d x\) 推出 \(\varphi(2)>\varphi(\xi_1)\)。在区间 \([1,2]\) 上使用拉格朗日中值定理得到 \(\varphi'(\xi_2)=\varphi(2)-\varphi(1)>0\)（\(\xi_2 \in (1,2)\)），思路正确。在区间 \([2,\xi_1]\) 上使用拉格朗日中值定理时，第二次识别结果正确写出差商分母为 \((\xi_1-2)\)（即 \(\varphi'(\xi_3)=\frac{\varphi(\xi_1)-\varphi(2)}{\xi_1-2}<0\)，\(\xi_3 \in (2,\xi_1)\)），但第一次识别误写为乘以1（即分母错误），但根据上下文可判断为误写（识别错误），且第二次识别正确，因此不扣分。最后对 \(\varphi'(x)\) 在 \([\xi_2,\xi_3]\) 上使用拉格朗日中值定理得到 \(\varphi''(\xi)=\frac{\varphi'(\xi_3)-\varphi'(\xi_2)}{\xi_3-\xi_2}<0\)，由于分子负、分母正，故 \(\varphi''(\xi)<0\)，且 \(\xi \in (\xi_2,\xi_3) \subset (1,3)\)，结论正确。整体逻辑严密，与标准答案等价，因此得5分。

题目总分：0+5=5分