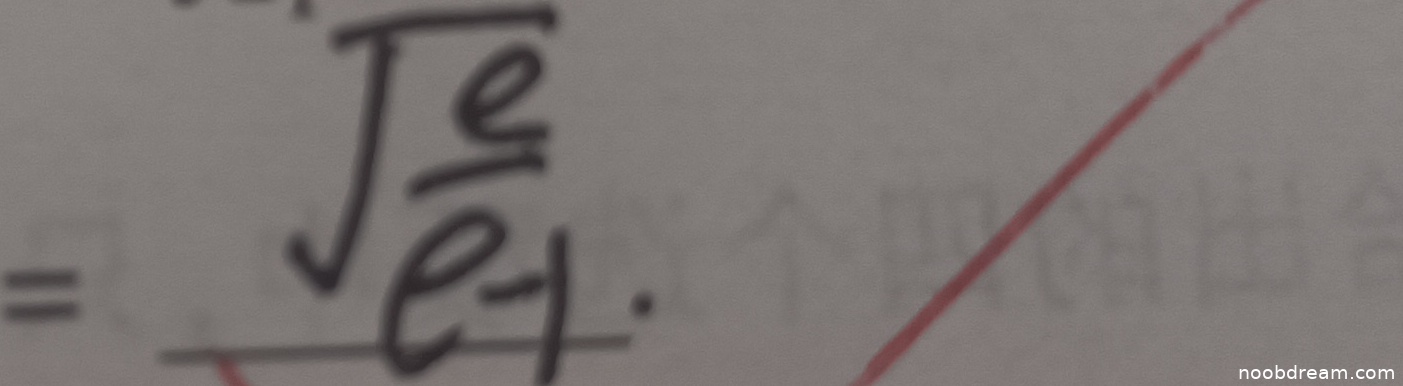
评分及理由

（1）得分及理由（满分4分）

学生两次识别结果分别为 \(\frac{\sqrt{e}}{e - 1}\) 和 \(\sqrt{\frac{e}{e - 1}}\)。标准答案为 \(\frac{1}{\sqrt{1-e^{-1}}}\)。首先，分析标准答案的推导过程：反函数在 \(y=0\) 处的导数为 \(\frac{1}{f'(x_0)}\)，其中 \(f(x_0)=0\)。由 \(f(x)=\int_{-1}^{x} \sqrt{1-e^{t}} d t\)，得 \(f(-1)=0\)，即 \(x_0=-1\)。计算 \(f'(-1)=\sqrt{1-e^{-1}}\)，因此 \(\left.\frac{d x}{d y}\right|_{y=0}=\frac{1}{\sqrt{1-e^{-1}}}\)。

学生答案 \(\frac{\sqrt{e}}{e - 1}\) 和 \(\sqrt{\frac{e}{e - 1}}\) 均与标准答案形式不同。化简标准答案：\(\frac{1}{\sqrt{1-e^{-1}}} = \frac{1}{\sqrt{\frac{e-1}{e}}} = \sqrt{\frac{e}{e-1}}\)，这与第二次识别结果 \(\sqrt{\frac{e}{e - 1}}\) 完全一致。因此，第二次识别结果正确。

根据打分要求，两次识别中只要有一次正确即不扣分。故本题得满分4分。

题目总分：4分