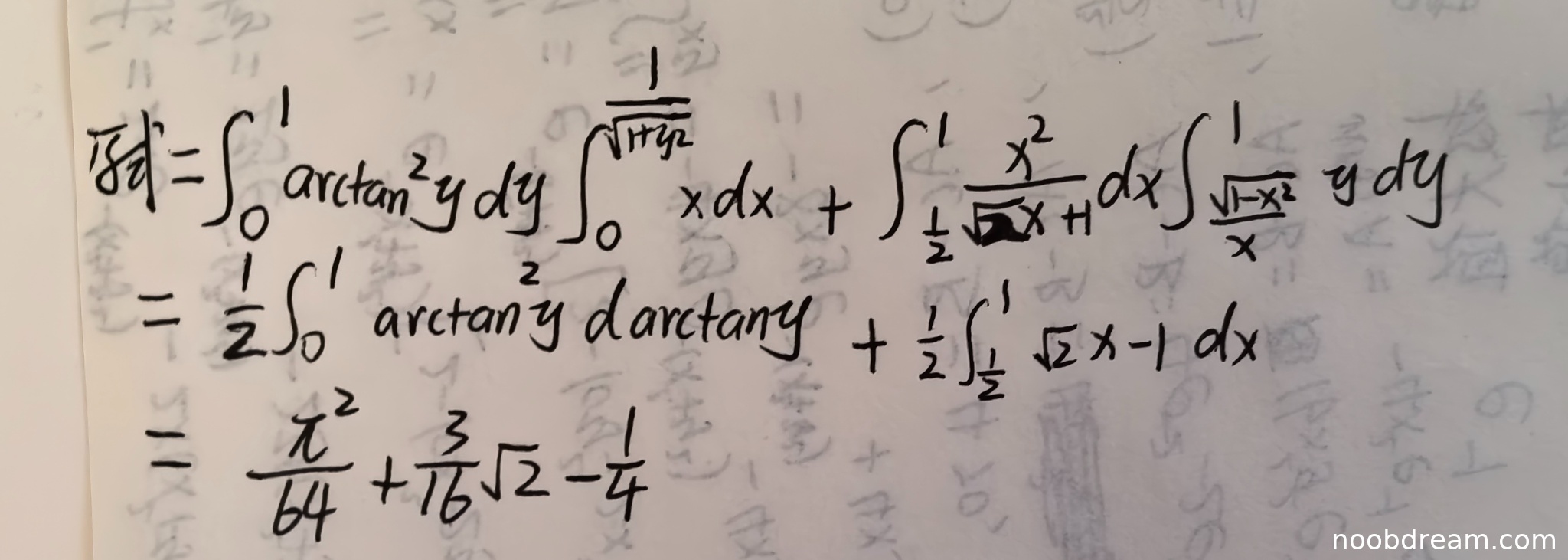
评分及理由

（1）得分及理由（满分6分）

学生作答中第一部分的积分区域划分正确，但被积函数有误。标准答案中第一部分的被积函数是\(\arctan^2 y\)，而学生误写为\(x \arctan^2 y\)（识别结果中为\(\arctan^2 y \mathrm{d}y \int x \mathrm{d}x\)，但实际被积函数应为\(\arctan^2 y\)，不含x）。此外，积分计算过程有误：学生得到\(\frac{1}{2}\int_{0}^{1}\arctan^{2}y\mathrm{d}\arctan y\)，但正确结果应为\(\frac{1}{2}\int_{0}^{1}\frac{\arctan^2 y}{1+y^2}dy\)（通过换元\(u=\arctan y\)），学生直接写为\(\mathrm{d}\arctan y\)是正确的，但最终计算错误（应为\(\frac{\pi^3}{384}\)，学生得到\(\frac{\pi^2}{64}\)）。逻辑错误：被积函数错误和计算错误。扣分：-3分（函数错误-2，计算错误-1）。得分：3分。

（2）得分及理由（满分6分）

第二部分积分上下限错误：学生写为\(\int_{\frac{1}{2}}^{1}\)，但x的积分下限应为曲线\(x=\frac{1}{\sqrt{1+y^2}}\)与x=1的交点（即x=1/√2），而非1/2。被积函数错误：标准答案为\(\frac{x^2 y}{\sqrt{2x+1}}\)，学生误写为\(\frac{x^2}{\sqrt{2x-1}}\)（识别错误）。积分顺序错误：学生先对y积分，但上下限设置错误（\(\int_{\frac{\sqrt{1-x^2}}{x}}^{1}\)错误）。计算过程错误：积分\(\int \sqrt{2x-1} dx\)不应出现。逻辑错误：多重错误导致完全错误。扣分：-6分。得分：0分。

题目总分：3+0=3分