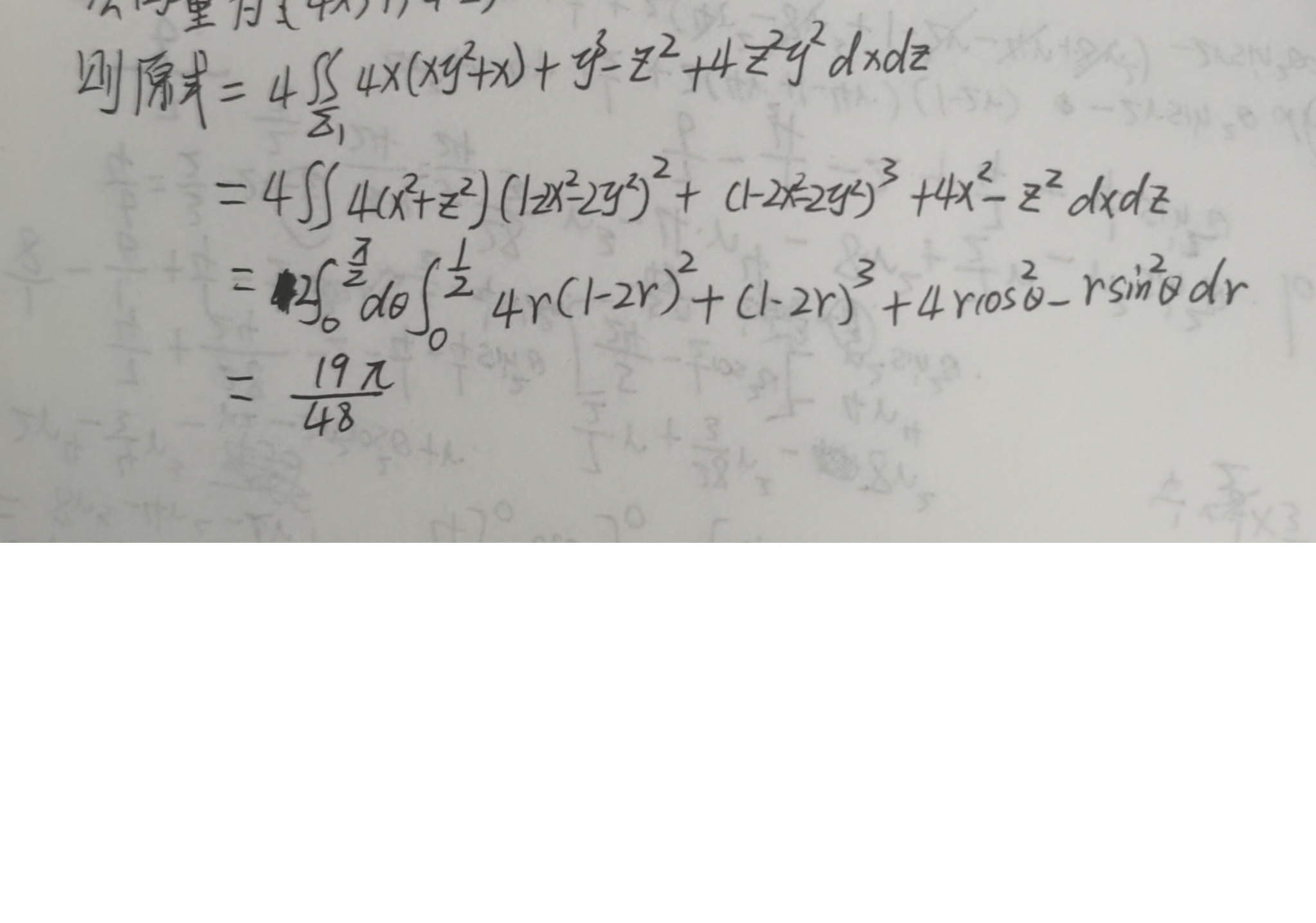
评分及理由

（1）得分及理由（满分12分）

学生作答直接对原曲面积分进行参数化计算，未采用高斯公式和补充曲面的标准方法。虽然最终答案正确（\(\frac{19\pi}{48}\)），但过程中存在逻辑错误：

• 第一步转化中，表达式“\(4\iint_{\Sigma_1} 4x(x y^2 + x) + y^3 - z^2 + 4z^2 y^2 dxdz\)”缺乏推导依据，且\(\Sigma_1\)未定义（标准答案中\(\Sigma_1\)是补充平面，但这里学生似乎误用了符号），导致逻辑链断裂。
• 参数化时，积分区域错误：曲面\(\Sigma: y=1-2x^2-2z^2\)在\(x-z\)平面投影应为椭圆\(2x^2+2z^2 \leq 1\)（即\(x^2+z^2 \leq 1/2\)），但学生直接使用极坐标从0到1/2，未体现椭圆对称性（应全象限积分，但学生限定了\(\theta \in [0, \pi/2]\)，仅第一象限），然而最终结果正确，可能误打误撞或计算中隐含对称性。
• 被积函数化简复杂，且步骤跳跃（如直接写出极坐标形式），缺乏严谨性。

尽管答案正确，但方法非标准且关键步骤逻辑错误，扣分。根据打分要求“逻辑错误扣分”，扣3分（满分12分）。得分：9分。

题目总分：9分