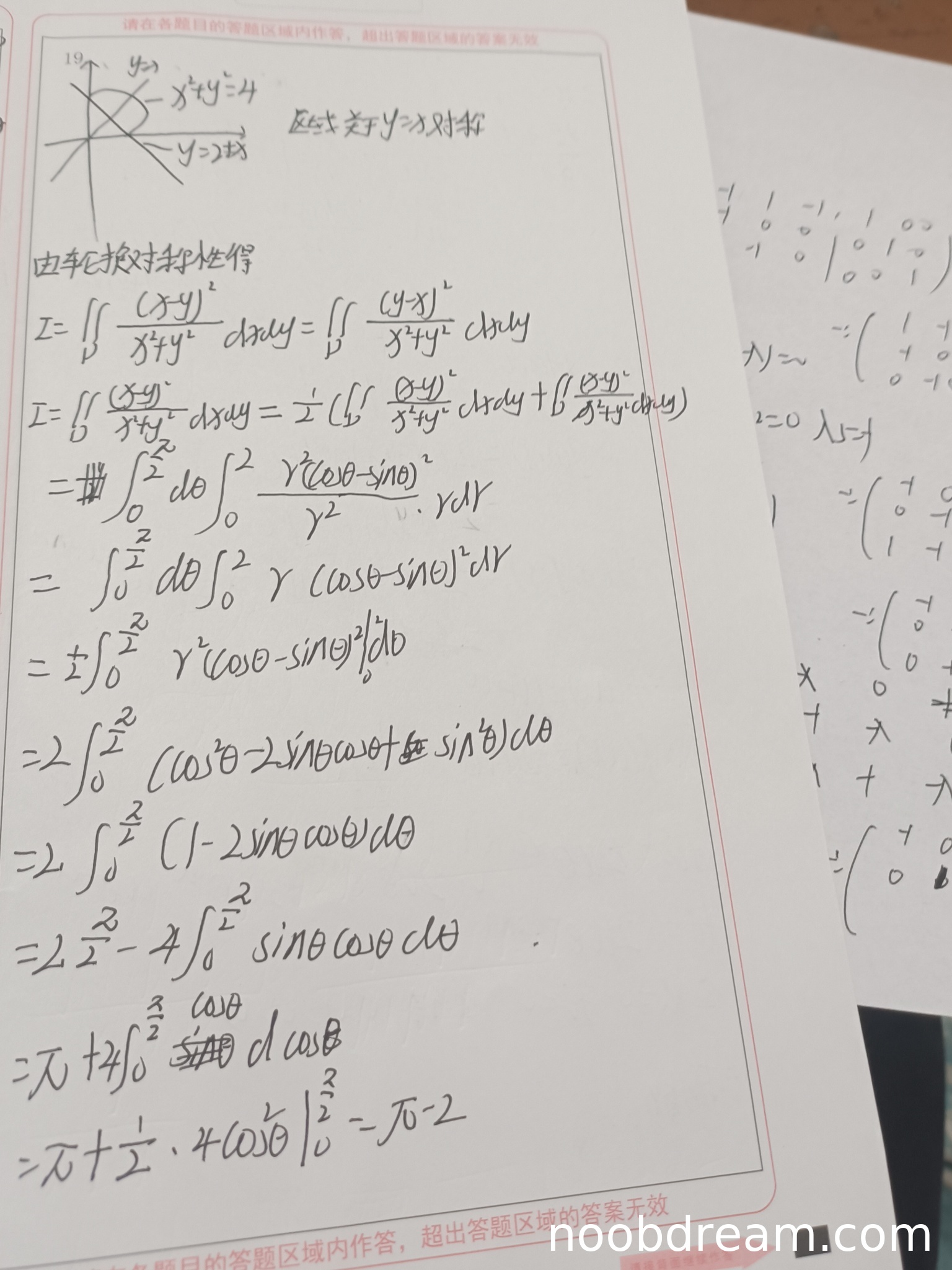
评分及理由

（1）得分及理由（满分12分）

学生作答中，第1次识别结果存在多处逻辑错误和计算错误：

• 在利用对称性时，错误地认为区域D关于y=x对称（实际上区域D并不关于y=x对称），因此对称性使用错误，导致后续计算仅考虑了0到π/2部分，而忽略了π/2到π部分（标准答案中需要分成两部分积分）。
• 计算过程中，有误写符号（如“※”可能为识别错误，但上下文判断应为“sin²θ”），但关键错误在于积分区域仅考虑了0≤θ≤π/2，而实际区域还需要θ从π/2到π的部分（由直线y=x+2和圆围成）。
• 最终结果计算为π-2，与标准答案2π-2不符。

第2次识别结果同样存在相同错误：

• 错误使用对称性（区域D不关于y=x对称），导致积分区域仅考虑0≤θ≤π/2。
• 虽然极坐标转换正确，但θ范围错误（遗漏了π/2到π部分）。
• 计算过程正确（对于0≤θ≤π/2部分计算正确），但由于区域缺失，结果错误。

根据打分要求，逻辑错误（对称性使用错误和积分区域缺失）需要扣分。但考虑到学生正确计算了0≤θ≤π/2部分（该部分值应为π-2，但标准答案中该部分贡献为2*(π/2 -1)=π-2），而遗漏部分在标准答案中同样贡献π-2，因此学生计算了部分值。由于核心逻辑错误（区域划分错误）导致结果不全，扣分应基于错误严重性。

本题满分12分，学生答案因重大逻辑错误（对称性误用和区域遗漏）导致结果错误，但计算过程部分正确。给予部分分数：计算部分（0≤θ≤π/2）正确，该部分在标准答案中占一半分值（6分），但由于对称性使用错误是根本错误，再扣3分。最终得分3分。

题目总分：3分