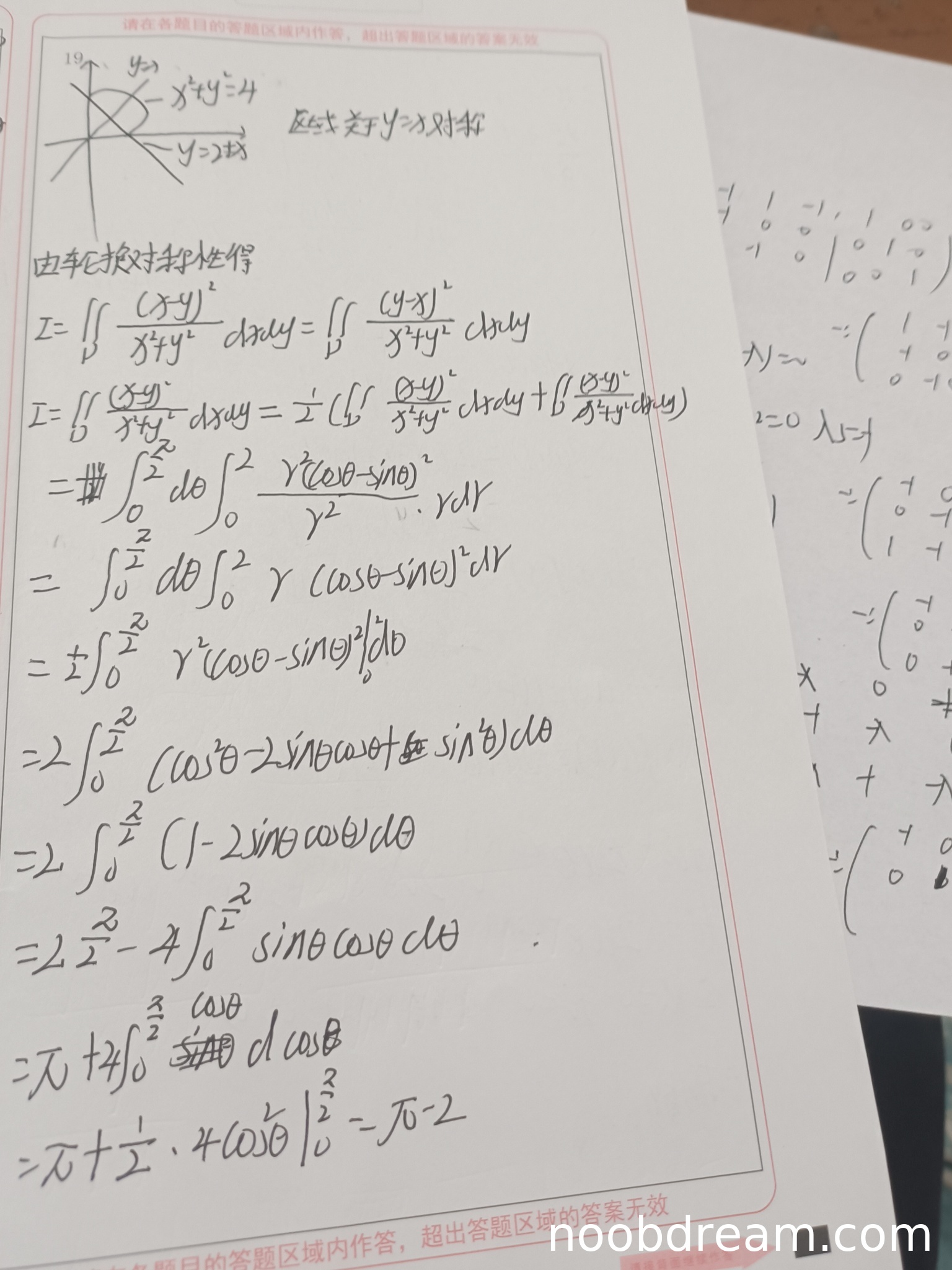
评分及理由

（1）得分及理由（满分12分）

学生作答中，第一次识别结果存在逻辑错误：在利用轮换对称性时，错误地认为I等于两个相同积分的平均值（实际上轮换对称性直接得到I=I，没有化简作用），且后续计算只考虑了第一象限（θ从0到π/2），但区域D实际包含第一和第二象限（标准答案中θ从0到π），因此漏掉了第二象限部分（θ从π/2到π）的积分。此外，第一次识别中计算过程有误（如“π + 4∫... dcosθ”步骤错误），导致错误结果π-2（实际应为2π-2）。第二次识别结果同样只计算了第一象限（θ从0到π/2），忽略了第二象限部分，且未正确使用对称性（轮换对称性在此题中无效，因为被积函数和区域均不满足对称条件），但计算过程正确（仅针对第一象限部分）。整体上，学生作答未完整覆盖积分区域，且对称性使用不当，但第二次识别的计算步骤（针对第一象限）正确。根据标准答案，完整积分应为2π-2，而学生得到π-2（仅第一象限结果），因此扣除区域遗漏和对称性错误的分数。扣分：区域遗漏（第二象限）扣6分，对称性错误扣2分，计算错误（第一次识别）已避免（以第二次识别为准），但第二次识别计算部分正确给部分分。最终得分：12 - 6（区域遗漏） - 2（对称性错误） = 4分。

题目总分：4分