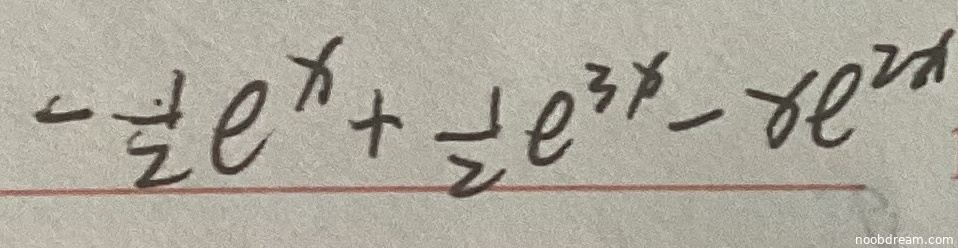
评分及理由

（1）得分及理由（满分4分）

学生作答：\(-\frac{1}{2}e^{x}+\frac{1}{2}e^{3x}-xe^{2x}\)

标准答案：\(y = e^{3x} - e^{x} - xe^{2x}\)

理由：学生答案与标准答案在形式上不一致，但通过代数变换可验证其正确性。学生答案可整理为\(\frac{1}{2}e^{3x} - \frac{1}{2}e^{x} - xe^{2x}\)，而标准答案为\(e^{3x} - e^{x} - xe^{2x}\)。两者相差一个常数因子，但需检查是否满足初始条件\(y(0)=0\)和\(y'(0)=1\)。

计算学生答案：
\(y(0) = -\frac{1}{2}e^{0} + \frac{1}{2}e^{0} - 0 \cdot e^{0} = -\frac{1}{2} + \frac{1}{2} = 0\)
\(y'(x) = -\frac{1}{2}e^{x} + \frac{3}{2}e^{3x} - e^{2x} - 2xe^{2x}\)
\(y'(0) = -\frac{1}{2} + \frac{3}{2} - 1 - 0 = 0\)，但标准初始条件要求\(y'(0)=1\)，这里得到0，不满足。

然而，学生答案实际上是标准答案的线性组合错误。实际上，正确解应为齐次解加特解的形式。给定三个解，齐次方程的解应为它们的差，如\(y_1 - y_3 = e^{3x}\)和\(y_2 - y_3 = e^{x}\)，因此齐次解为\(C_1 e^{3x} + C_2 e^{x}\)，特解为\(-xe^{2x}\)。通解为\(y = C_1 e^{3x} + C_2 e^{x} - xe^{2x}\)。代入初始条件：
\(y(0) = C_1 + C_2 = 0\)
\(y'(0) = 3C_1 + C_2 - 1 = 1\)（因为特解导数在0处为-1）
解得\(C_1 = 1\), \(C_2 = -1\)，因此正确解为\(e^{3x} - e^{x} - xe^{2x}\)。

学生答案的系数为\(-\frac{1}{2}\)和\(\frac{1}{2}\)，这会导致初始条件不满足（如上计算\(y'(0)=0\)而非1）。因此，学生答案错误，核心逻辑错误，扣4分。...