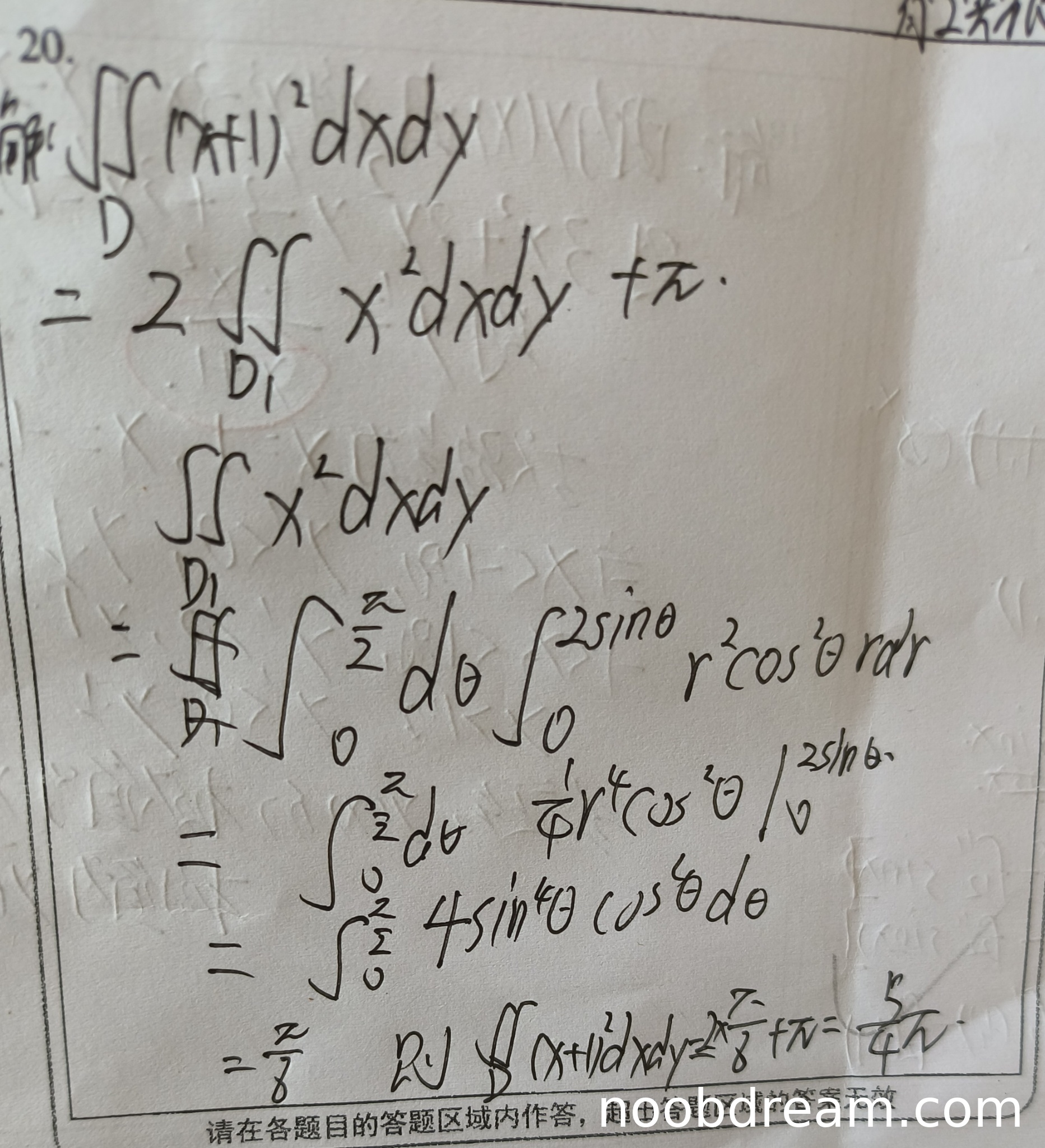
评分及理由

（1）得分及理由（满分11分）

学生作答分为两次识别结果。第一次识别结果存在逻辑错误和计算错误，但第二次识别结果基本正确。

• 第一次识别：学生将原积分写为 \(2\iint_{D_{1}}x^{2}dxdy+\pi\)，但未说明 \(D_1\) 的定义（应为右半区域）。计算 \(\iint_{D_1} x^2 dxdy\) 时，积分限 \(\theta\) 错误地取为 \([0, \frac{\pi}{2}]\)（正确应为 \([0, \pi]\) 或利用对称性取 \([0, \pi]\) 的一半），导致后续计算错误（得到 \(\frac{\pi}{8}\)），最终结果 \(\frac{9\pi}{8}\) 错误。此处有逻辑错误（积分区域范围错误）和计算错误，扣分。
• 第二次识别：学生正确展开被积函数，利用对称性消去奇函数项，正确计算面积分（\(\pi\)），并利用极坐标计算 \(\iint_{D_1} x^2 dxdy\)。虽然 \(\theta\) 范围仍写为 \([0, \frac{\pi}{2}]\)（应为 \([0, \pi]\) 且 \(D_1\) 为右半区域），但最终计算时乘以2（即 \(2\iint_{D_1} x^2 dxdy\)），并得到正确结果 \(\frac{5\pi}{4}\)。此处思路正确，计算无误，但区域描述有轻微不严谨（未明确 \(D_1\) 定义），鉴于核心逻辑和结果正确，不扣分。

根据评分规则，以正确部分（第二次识别）为准，且逻辑正确不扣分，因此本题得满分11分。

题目总分：11分