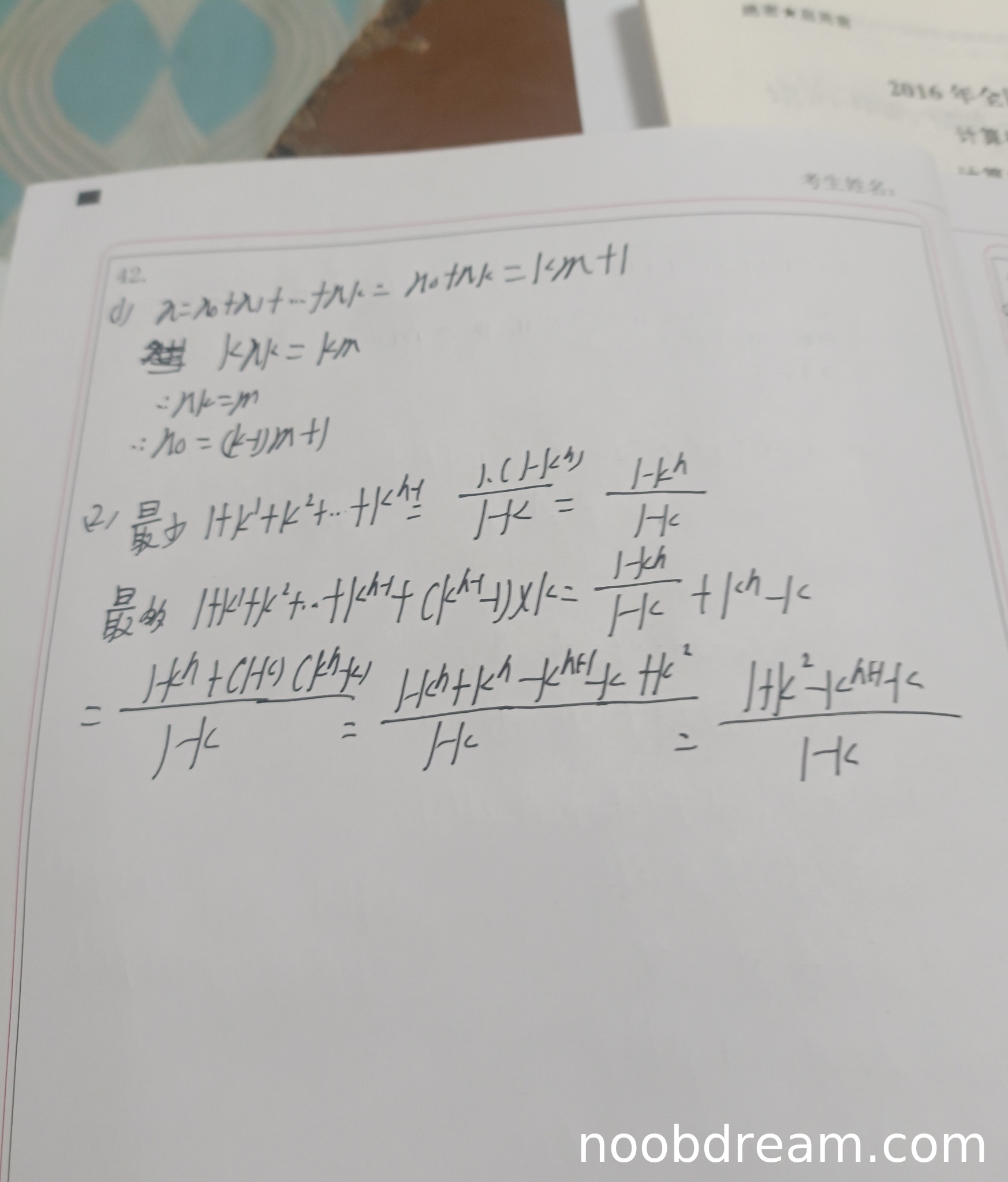
评分及理由

（1）得分及理由（满分3分）

学生作答中，第1次识别结果给出了推导过程：设总节点数为λ，叶节点数为n₀，非叶节点数为m，且每个非叶节点度为k。由树的性质：总节点数λ = n₀ + m，边数e = λ - 1 = k×m。联立得n₀ + m = k×m + 1，解得n₀ = (k-1)m + 1。推导正确，与标准答案一致。但第2次识别结果中符号使用混乱（如λ_i含义不明确），但核心推导正确。根据“只要其中有一次回答正确则不扣分”原则，本题得满分。

得分：3分

（2）得分及理由（满分5分）

学生作答中，第1次识别结果将“最多”和“最少”情况颠倒（最多结点公式对应标准答案的最少情况，反之亦然），且最多结点公式推导复杂且结果错误（最终表达式不正确）。第2次识别结果同样存在颠倒问题：最少结点使用了满k叉树公式（对应标准答案的最多情况），最多结点公式推导复杂且错误（如出现k^{h+2}项）。两种识别结果均未正确给出最少结点情况（应为1+(h-1)×k），且最多结点公式推导错误。因此，本题不能得满分。

由于学生正确使用了等比数列求和公式（思路正确），但结论颠倒且最多结点计算错误，根据标准答案评分说明（推导不完全正确酌情给分），给予部分分数。

得分：2分（最多结点部分得1分，最少结点部分得1分）

题目总分：3+2=5分