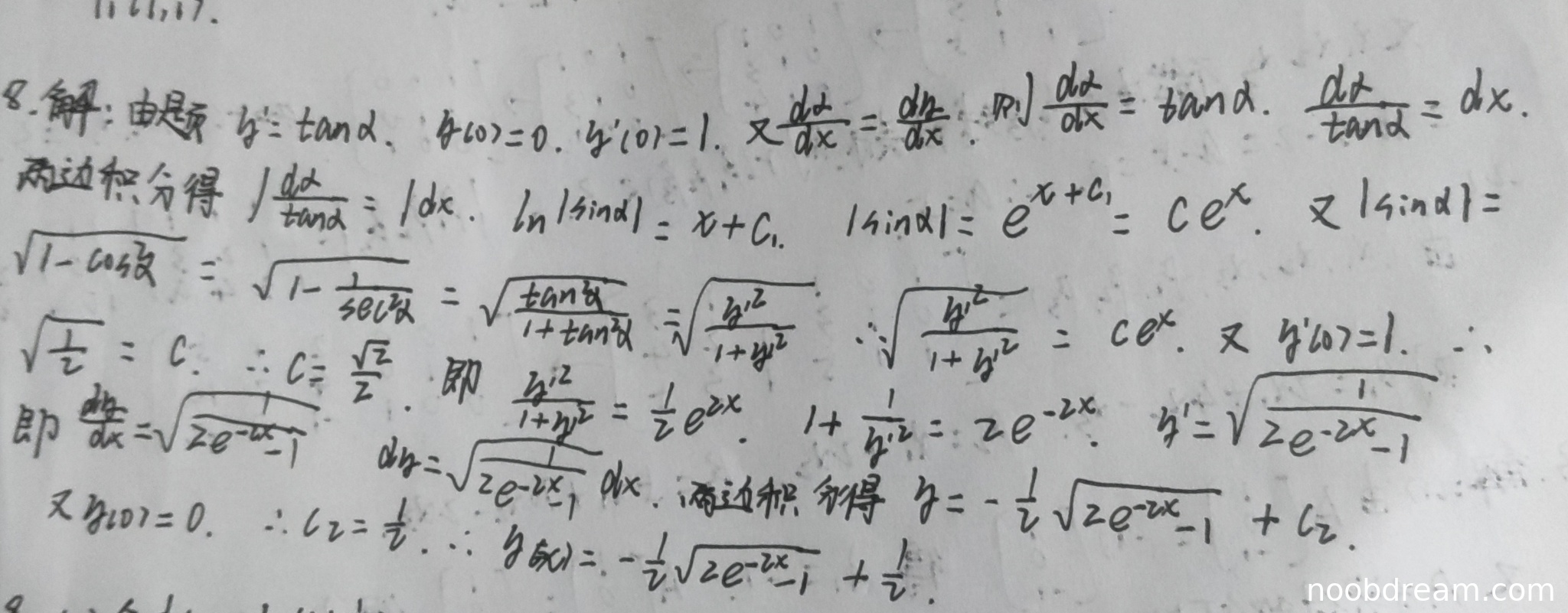
评分及理由

（1）得分及理由（满分10分）

本题满分10分。学生的解答过程存在多处逻辑错误。

首先，在两次识别结果中，学生都将题目中的条件 \(\frac{d\alpha}{dx} = \frac{dy}{dx}\) 错误地理解或书写为 \(\frac{dt}{dx} = \frac{dy}{dx}\) 或 \(\frac{dt}{dx} = \frac{dy'}{dx}\)。这是一个根本性的逻辑错误，因为它改变了微分方程的结构。标准答案中由 \(\tan \alpha = y'\) 和 \(\frac{d\alpha}{dx} = y'\) 推导出 \(y'' = y' + (y')^3\)，而学生的错误起点导致后续推导全部偏离正确方向。

其次，学生的求解过程从错误的方程 \(\frac{dt}{\tan t} = dx\) 开始积分，并试图将 \(\sin t\) 与 \(y'\) 建立关系。虽然其中关于 \(\sin t\) 与 \(y'\) 的三角恒等变换（\(\sqrt{y'^2/(1+y'^2)}\)）本身是正确的数学运算，但由于出发点错误，整个推导过程失去了意义。

最后，学生得到的最终答案 \(y(x)=-\frac{1}{2}\sqrt{2e^{-2x}-1}+\frac{1}{2}\) 与标准答案 \(y(x) = \arcsin\left(\frac{\sqrt{2}}{2}e^x\right) - \frac{\pi}{4}\) 完全不同。通过简单验证可知，学生的答案不满足初始条件 \(y'(0)=1\)（计算其导数在x=0处为无穷大），这说明答案是完全错误的。

由于学生的解答在核心逻辑（建立微分方程）上存在严重错误，并且最终答案错误，只能给予步骤分。考虑到学生正确写出了初始条件 \(y(0)=0, y'(0)=1\)，并尝试了积分求解，给予1分。

得分：1分

题目总分：1分