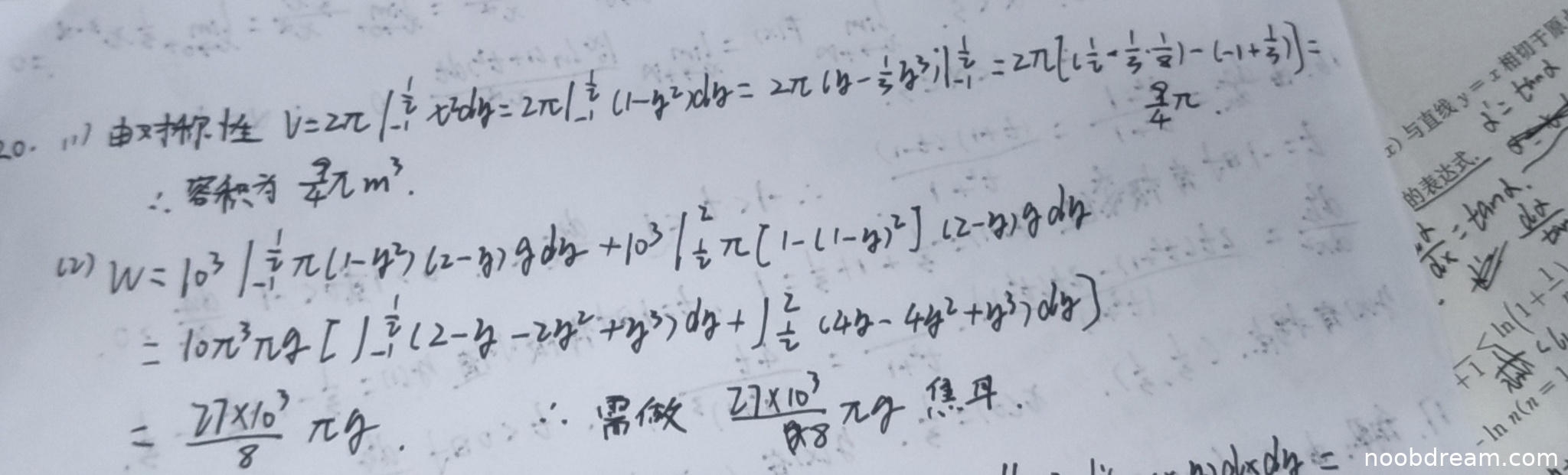
评分及理由

（Ⅰ）得分及理由（满分5分）

学生答案：

• 第一次识别：使用对称性，积分区间为[-1, 1/2]，被积函数为πx²=π(1-y²)，计算正确，结果9π/4正确。
• 第二次识别：与第一次基本一致，结果正确。

标准答案：使用旋转体体积公式，积分区间为[1/2, 1]，被积函数为πx²=π(1-y²)，并乘以2（对称性），结果9π/4。

分析：学生思路与标准答案不同但正确。学生从y=-1积分到y=1/2（下半圆），利用了x²+y²=1的完整圆对称性，而标准答案从y=1/2积分到y=1（上半圆）再乘2。两者等价，计算结果正确。

扣分：无逻辑错误，计算正确。

得分：5分

（Ⅱ）得分及理由（满分6分）

学生答案：

• 功的计算公式W=∫ρg·πx²(y)·(2-y)dy正确。
• 分区积分：第一段y从-1到1/2，对应曲线x²+y²=1，x²=1-y²正确；第二段y从1/2到2，对应曲线x²+y²=2y，解出x²=2y-y²正确。
• 但第二段被积函数中，学生写的是π[1-(1-y)²]=π(2y-y²)，正确。
• 计算过程：学生将积分拆开并计算，但最终结果27×10³πg/8与标准答案27×10³πg/4不一致。

标准答案：积分区间应为从y=1/2到y=2（上半部分）和从y=1/2到y=1（下半部分？标准答案描述不清），但结果应为27π×10³g/4。

分析：

• 学生分区正确，被积函数正确。
• 但第一段积分区间应为y从-1到1/2？容器实际水满时，y范围应从最低点到最高点。容器由曲线绕y轴旋转，从图形看，y从-1到2？但学生第一段从-1到1/2，第二段从1/2到2，覆盖了y从-1到2，这是完整的容器高度？实际上，容器底部在y=-1？但题目中曲线定义y≥1/2和y≤1/2，可能图形有误？根据描述，容器应由两部分曲线连接而成，y从1/2到2（上半球）和y从-1到1/2（下半球）？学生按y从-1到2积分，思路正确。
• 计算错误：学生最终结果27×10³πg/8比标准答案小一半，可能是在积分计算中出现算术错误。例如，积分∫(2-y-2y²+y³)dy从-1到1/2和∫(4y-4y²+y³)dy从1/2到2，计算值有误。

扣分：计算结果错误，扣2分（结果错误一般扣一半分数，本题满分6分，扣2分）。

得分：4分

题目总分：5+4=9分