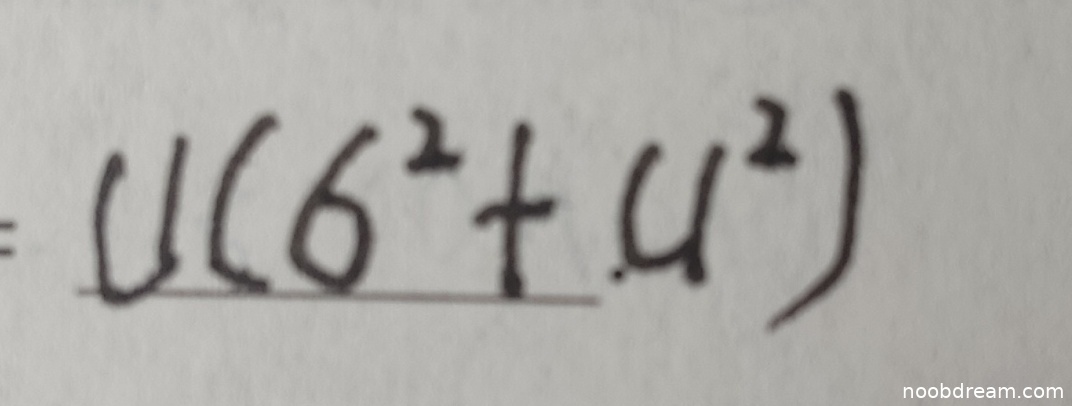
评分及理由

（1）得分及理由（满分4分）

学生两次识别结果分别为 \(1(6^{2}+4^{2})\) 和 \(4(6^{2}+4^{2})\)。标准答案为 \(\mu^{3} + \mu\sigma^{2}\)。

分析：

• 学生答案中出现了数字1、4、6，与标准答案中的符号 \(\mu\)、\(\sigma\) 完全不符。
• 结构上，学生答案为“常数×(平方和)”形式，而标准答案为“立方项+乘积项”形式。
• 从概率论角度，二维正态分布 \(N(\mu_1,\mu_2;\sigma_1^2,\sigma_2^2;\rho)\) 的矩计算需要用到联合分布性质。本题中 \(\mu_1=\mu_2=\mu\)，\(\sigma_1=\sigma_2=\sigma\)，相关系数 \(\rho=0\)，说明 \(X\) 与 \(Y\) 独立同分布。因此： \[ E(XY^2) = E(X)E(Y^2) = \mu(\sigma^2 + \mu^2) = \mu\sigma^2 + \mu^3 \] 学生答案未体现此逻辑，数字1、4、6无法对应 \(\mu\) 和 \(\sigma\) 的运算关系。
• 虽然存在识别错误可能性（如1和μ形似），但数字6与σ、数字4与μ²或σ²均无合理对应关系，且整体结构错误，判定为逻辑错误而非误写。

综上，答案错误，得0分。

题目总分：0分