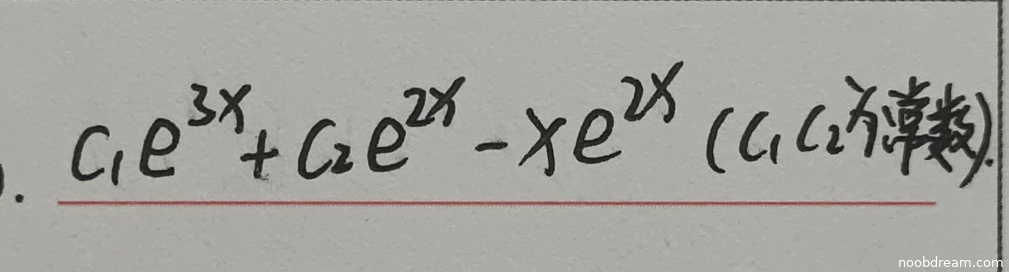
评分及理由

（1）得分及理由（满分4分）

学生两次识别的答案均为 \(C_{1}e^{3x}+C_{2}e^{2x}-xe^{2x}\)（或 \(c_{1}e^{3x}+c_{2}e^{2x}-xe^{2x}\)）。

标准答案为 \(y=c_{1}(e^{3x}-e^{x})+c_{2}e^{x}-xe^{2x}\)。

分析：

1. 题目给出了三个解 \(y_1, y_2, y_3\)，要求二阶常系数非齐次线性微分方程的通解。通解的结构应为：对应齐次方程的通解 + 非齐次方程的一个特解。

2. 首先需要找到非齐次方程的一个特解。观察三个解，发现 \(y_3 = -xe^{2x}\) 是三者中最简单的形式，且 \(y_1 - y_3 = e^{3x}\)，\(y_2 - y_3 = e^{x}\)。这表明 \(e^{3x}\) 和 \(e^{x}\) 都是对应齐次方程的解。

3. 由于是二阶方程，齐次方程的通解应由两个线性无关的解构成。\(e^{3x}\) 和 \(e^{x}\) 是线性无关的，因此齐次方程的通解为 \(C_1 e^{3x} + C_2 e^{x}\)。

4. 因此，原非齐次方程的通解应为：齐次通解 + 非齐次特解 = \(C_1 e^{3x} + C_2 e^{x} - xe^{2x}\)。

5. 学生的答案是 \(C_{1}e^{3x}+C_{2}e^{2x}-xe^{2x}\)。其中，齐次部分的解被写成了 \(e^{3x}\) 和 \(e^{2x}\)。然而，根据题目给出的解，\(e^{2x}\) 并不是对应齐次方程的解（因为没有任何两个给定的解的差是 \(e^{2x}\) 的常数倍）。这是一个根本性的逻辑错误，表明学生没有正确分析出齐次方程的解。

6. 学生的答案与标准答案在齐次解部分存在本质差异，且其齐次解 \(e^{2x}\) 的选取是错误的。

因此，该答案不正确。

得分：0分

题目总分：0分