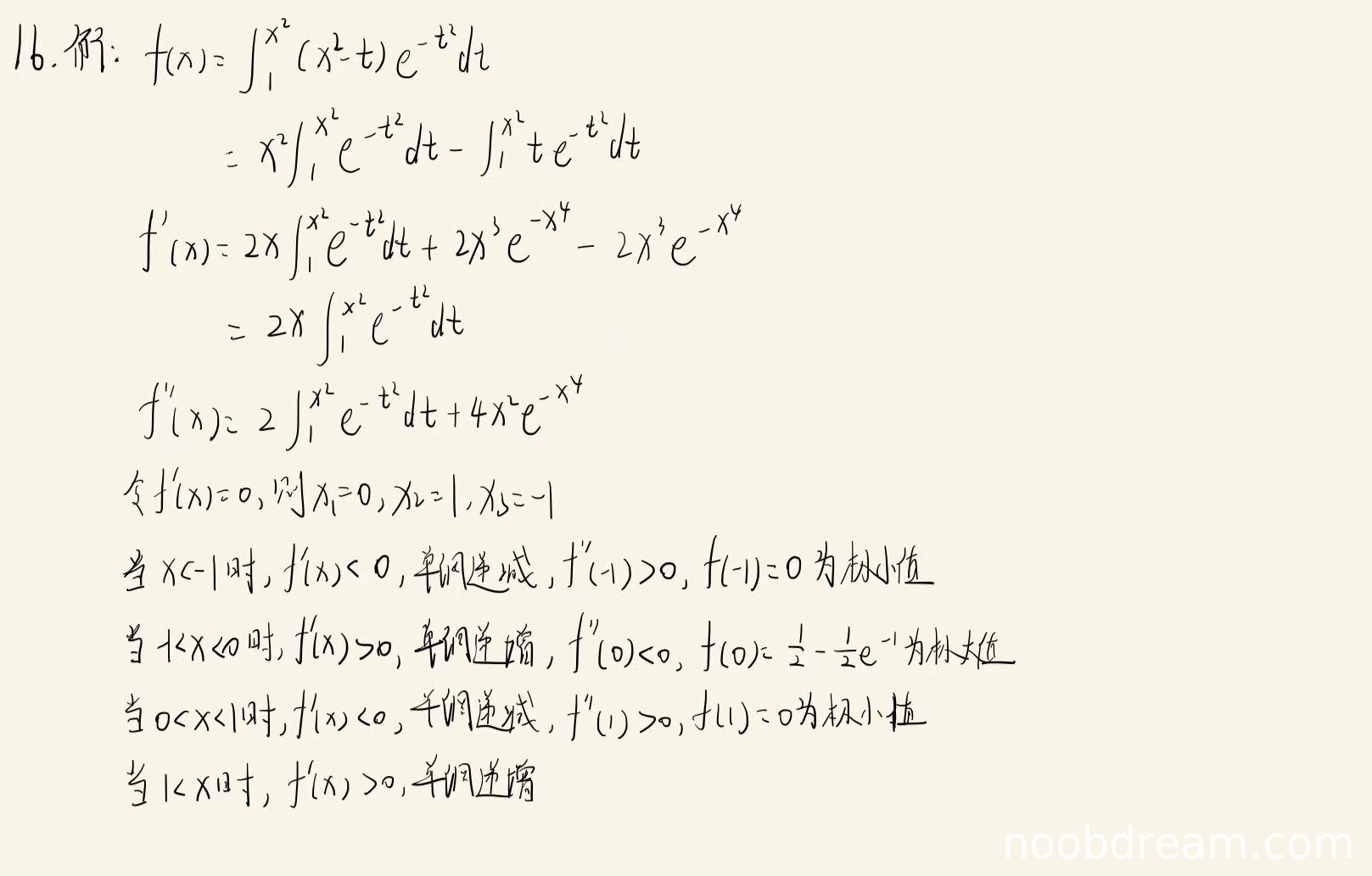
评分及理由

（1）导数计算（满分2分）

学生正确计算了导数 \( f'(x) = 2x \int_{1}^{x^{2}} e^{-t^{2}} dt \)，过程清晰。得2分。

（2）驻点求解（满分2分）

学生正确解出驻点 \( x = 0, \pm 1 \)。得2分。

（3）单调区间判断（满分3分）

学生正确分析了各区间导数的符号，得出单调递增区间为 \((-1,0)\) 和 \((1,+\infty)\)，单调递减区间为 \((-\infty,-1)\) 和 \((0,1)\)。得3分。

（4）极值计算（满分3分）

学生正确计算出极值点函数值：\( f(\pm 1) = 0 \)，\( f(0) = \frac{1}{2} - \frac{1}{2}e^{-1} \)。但在判断极值类型时使用了二阶导数检验，虽然结果正确，但方法不是最简。考虑到二阶导数检验在此题中也能得出正确结论，且极值计算结果完全正确，不扣分。得3分。

题目总分：2+2+3+3=10分