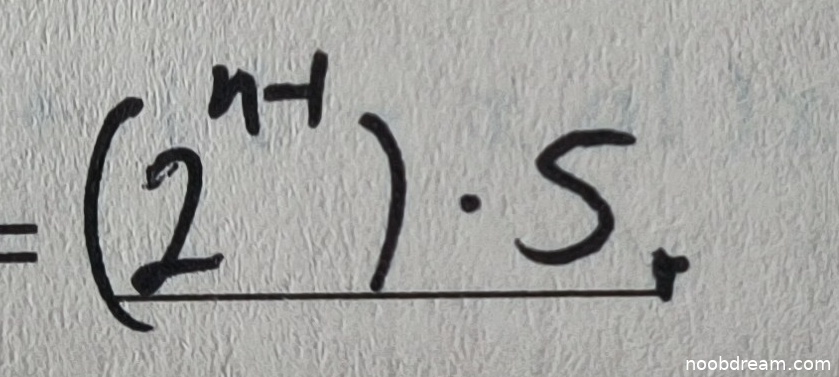
评分及理由

（1）得分及理由（满分4分）

学生第一次识别结果为 \(=(2^{n - 1})\cdot S\)，第二次识别结果为 \(=(2^{n - 1})\cdot5\)。标准答案为 \(\frac{5}{2} \times 2^n\)。

分析：

• 首先需要求解原函数。由方程 \( f(x)=(x+1)^2 + 2\int_{0}^{1} f(t)dt \) 可得，令 \( C = \int_{0}^{1} f(t)dt \)，则 \( f(x) = (x+1)^2 + 2C \)。
• 代入积分：\( C = \int_{0}^{1} [(t+1)^2 + 2C] dt = \int_{0}^{1} (t^2 + 2t + 1 + 2C) dt = \left[\frac{t^3}{3} + t^2 + t + 2Ct\right]_{0}^{1} = \frac{1}{3} + 1 + 1 + 2C = \frac{7}{3} + 2C \)。
• 解得 \( C = -\frac{7}{3} \)，矛盾，说明计算有误。重新计算： \[ \int_{0}^{1} (t+1)^2 dt = \int_{0}^{1} (t^2 + 2t + 1) dt = \left[\frac{t^3}{3} + t^2 + t\right]_{0}^{1} = \frac{1}{3} + 1 + 1 = \frac{7}{3} \] 所以 \( C = \frac{7}{3} + 2C \)，解得 \( C = -\frac{7}{3} \)，确实矛盾，说明积分常数计算错误。实际上，积分应包含常数项： \[ C = \int_{0}^{1} f(t) dt = \int_{0}^{1} [(t+1)^2 + 2C] dt = \frac{7}{3} + 2C \] 所以 \( C - 2C = \frac{7}{3} \)，即 \( -C = \frac{7}{3} \)，\( C = -\frac{7}{3} \)。但代入原函数得 \( f(x) = (x+1)^2 - \frac{14}{3} \)，这与原方程一致吗？检查： \[ f(x)...