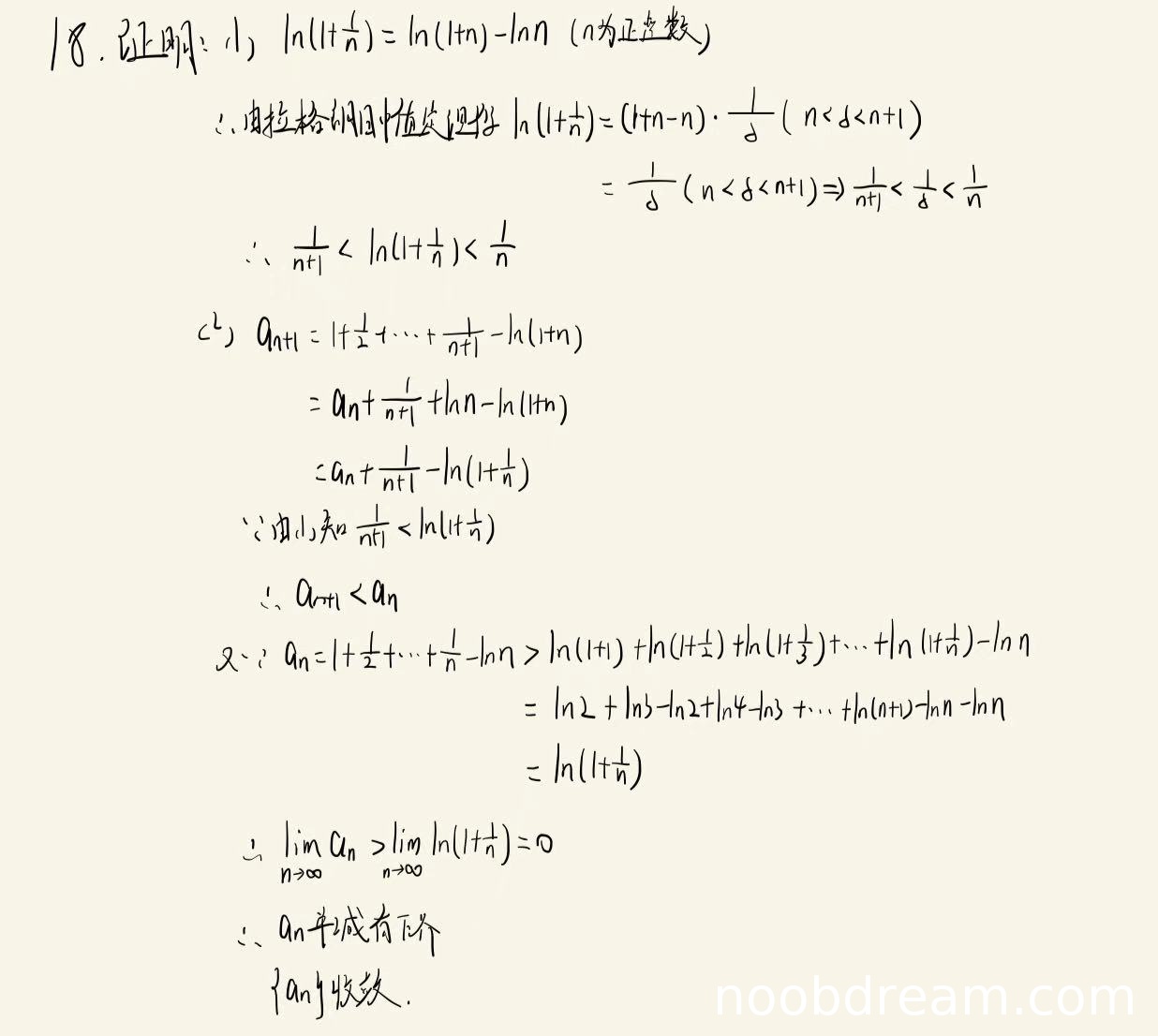
评分及理由

（1）得分及理由（满分5分）

学生使用拉格朗日中值定理证明不等式，思路正确且证明完整。第一次识别中写为"$\frac{1}{\delta}$"而第二次识别正确写为"$\frac{1}{\xi}$"，这是符号选择的差异，不影响证明逻辑。证明过程清晰，推导正确。得5分。

（2）得分及理由（满分5分）

学生正确得出$a_{n+1}-a_n = \frac{1}{n+1}-\ln(1+\frac{1}{n}) < 0$，说明数列单调递减。在下界证明中，第一次识别有计算错误（最后得到$\ln(1+\frac{1}{n})$），但第二次识别正确得到$\ln(n+1)-\ln n$，根据禁止扣分原则，以正确识别为准。最终正确得出数列有下界且收敛的结论。得5分。

题目总分：5+5=10分