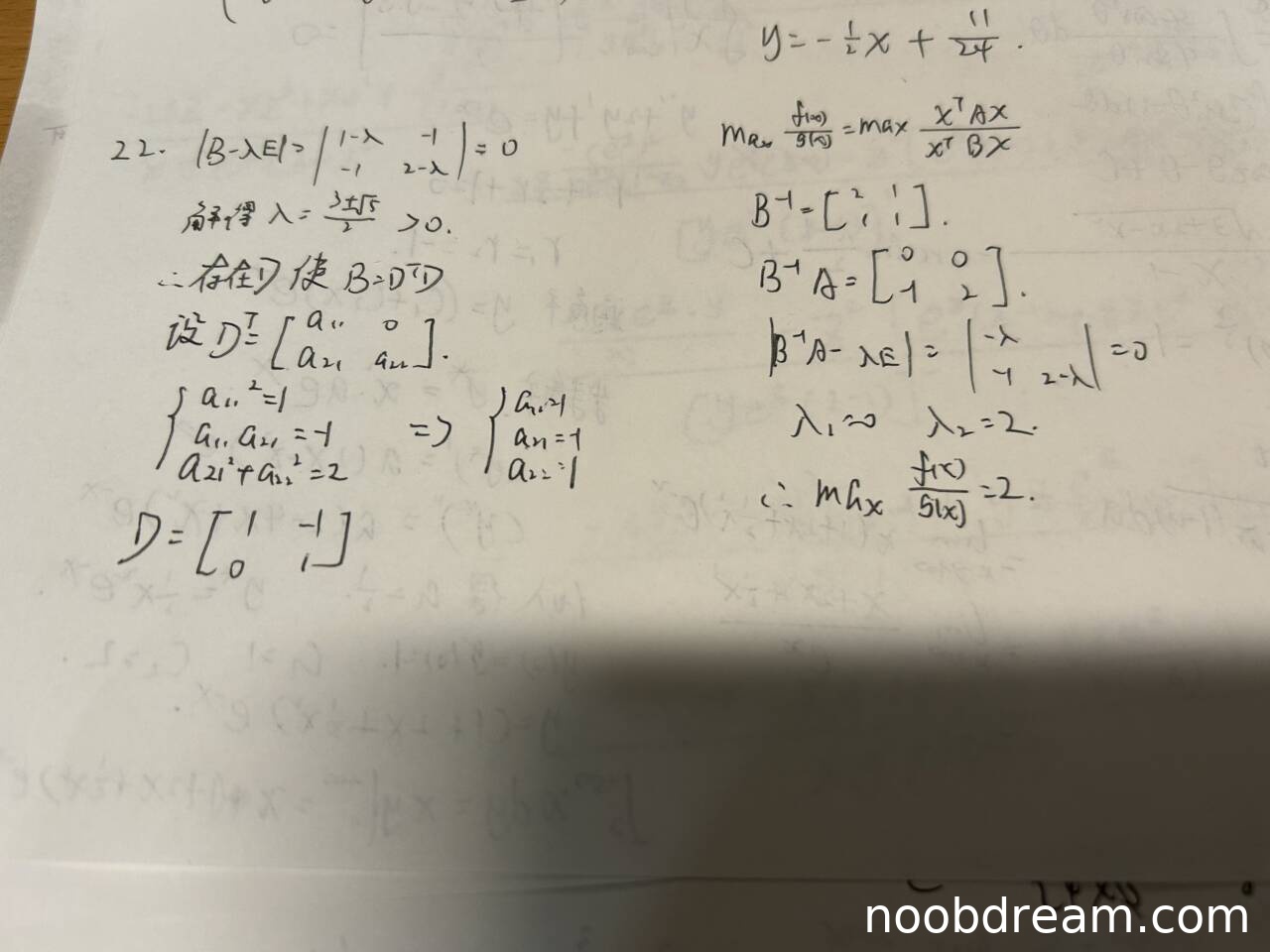
评分及理由

（1）得分及理由（满分6分）

学生首先通过计算矩阵B的特征值均为正，判断B正定，从而得出存在可逆矩阵D使B=D^T D，这一步正确。然后通过设D^T为下三角矩阵，解方程组得到D，方法正确且结果与标准答案一致。但学生在第一次识别中写的是“设D^T = [a11 0; a21 a22]”，而标准答案中D是上三角矩阵，这里学生设的是下三角的转置，即D本身是上三角，与标准答案一致，只是表述方式不同，因此不扣分。计算过程正确，最终得到D = [1 -1; 0 1]，与标准答案一致。但第一次识别中出现了无关内容“y = -1/2x + 11/24”，可能是识别错误，不影响核心逻辑，不扣分。因此本小题得满分6分。

（2）得分及理由（满分6分）

学生通过计算B^{-1}A的特征值来求max f(x)/g(x)，思路正确。但计算B^{-1}A时，第一次识别结果为[0 0; 1 2]，第二次识别结果为[0 0; -1 2]，而标准答案中未直接计算B^{-1}A，而是通过变换后求矩阵M的特征值。学生的方法本质是求广义特征值问题，即解|A - λB| = 0，等价于求B^{-1}A的特征值。但学生计算B^{-1}正确，为[2 1; 1 1]，而A矩阵应为[1 -2; -2 4]（f的二次型矩阵），计算B^{-1}A时，第一次识别结果[0 0; 1 2]错误，第二次识别结果[0 0; -1 2]正确（因为B^{-1}A = [2 1;1 1] * [1 -2;-2 4] = [0 0; -1 2]）。特征值计算正确，得到λ1=0, λ2=2，因此最大值为2，与标准答案一致。虽然第一次识别有计算错误，但第二次识别正确，且最终答案正确，根据规则“只要其中有一次回答正确则不扣分”，因此本小题得满分6分。

题目总分：6+6=12分