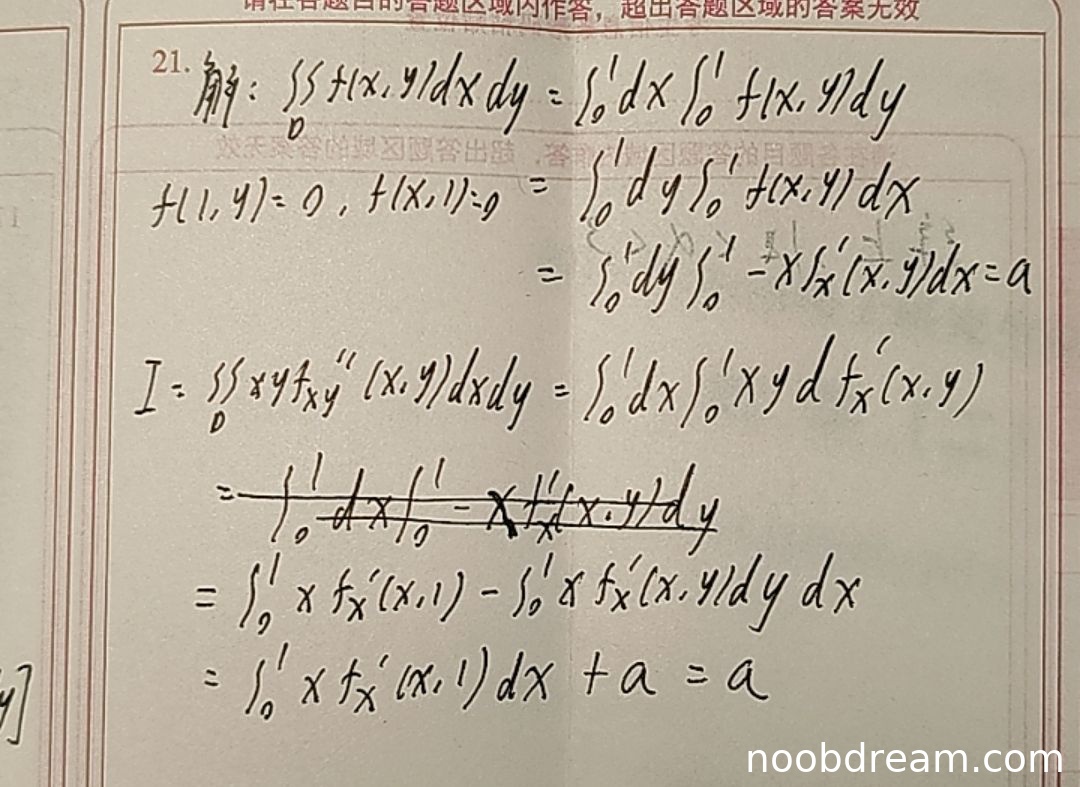
评分及理由

（1）得分及理由（满分11分）

学生作答的整体思路与标准答案一致，都是通过分部积分法将二重积分转化为已知条件。具体步骤：

• 第一步：将I写成累次积分形式 \(\int_{0}^{1}dx\int_{0}^{1} xy f_{xy}''(x,y)dy\) 正确
• 第二步：对y分部积分 \(\int_{0}^{1} xy df_x'(x,y)\) 正确
• 第三步：得到 \(\int_{0}^{1}dx\int_{0}^{1} -x f_x'(x,y)dy\) 正确
• 第四步：交换积分次序得到 \(- \int_{0}^{1}dy\int_{0}^{1} x f_x'(x,y)dx\) 正确
• 第五步：对x分部积分得到最终结果a

但在具体计算过程中存在一些逻辑错误：

• 在第三步到第四步的转换中，学生写成了 \(\int_{0}^{1}xf_x'(x,1)-\int_{0}^{1}xf_x'(x,y)dydx\)，这一步的推导不够严谨，边界项的处理不完整
• 最后直接得到 \(\int_{0}^{1}xf_x'(x,1)dx + a = a\)，这个等式缺乏充分论证

由于主要思路正确，且最终得到了正确结果，但推导过程中存在逻辑不严谨的地方，扣2分。

得分：9分

题目总分：9分